

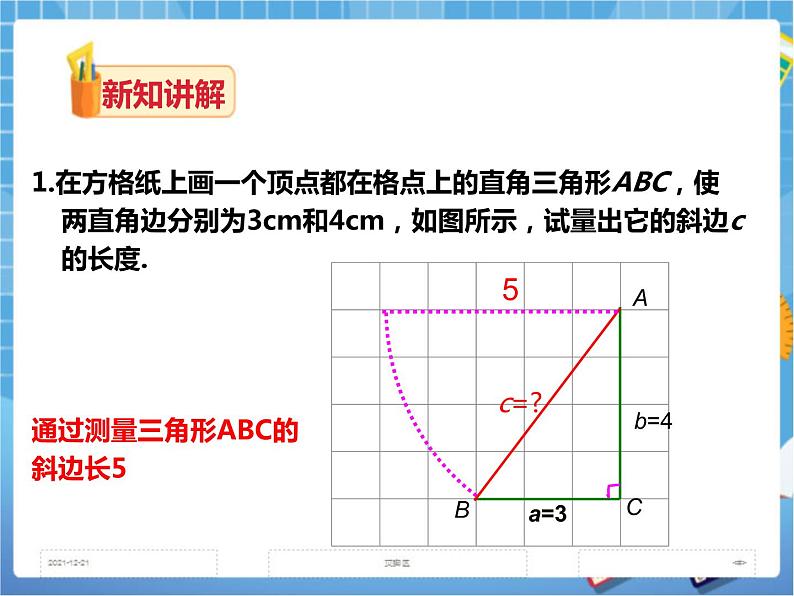
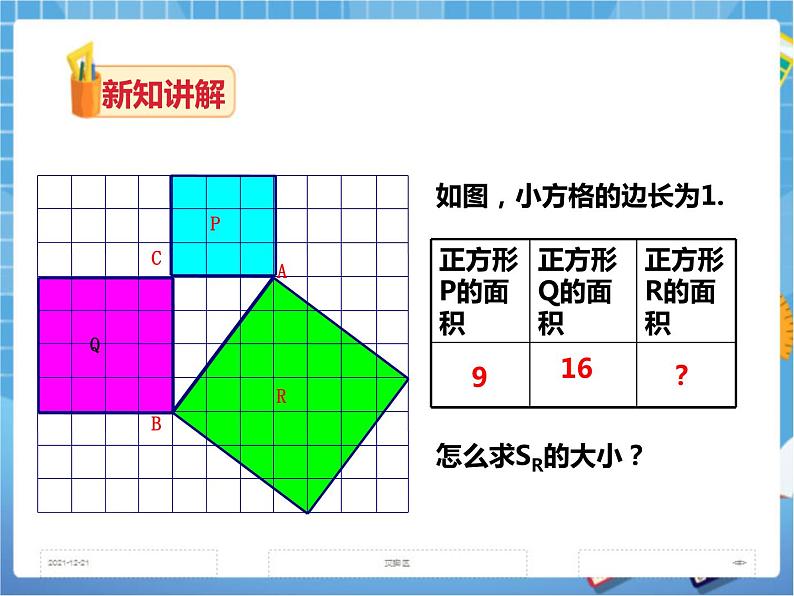
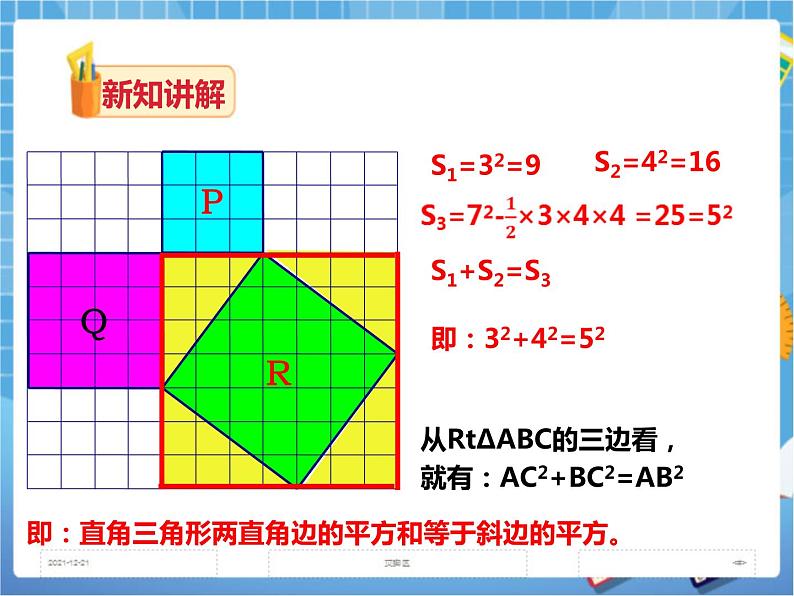
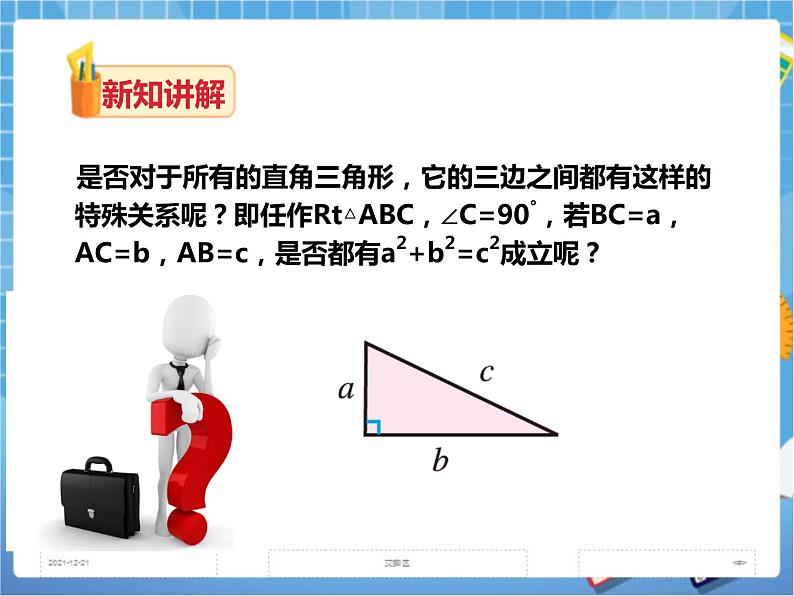







- 1.1直角三角形的性质和判定(1)(课件+教案+练习) 课件 45 次下载
- 1.1直角三角形的性质和判定(2)(课件+教案+练习) 课件 36 次下载
- 1.2.2直角三角形的性质和判定(课件+教案+练习) 课件 35 次下载
- 1.2直角三角形的性质和判定(3)(课件+教案+练习) 课件 35 次下载
- 1.3 直角三角形全等的判定(课件+教案+练习) 课件 35 次下载
初中数学湘教版八年级下册1.2 直角三角形的性质与判定(Ⅱ)评优课课件ppt
展开1.2.1直角三角形的性质与判定练习题
一、选择题
1. 如图,带阴影的矩形面积是( )平方厘米.
A.9 B.24 C.45 D.51
2、已知直角三角形两边的长为3和4,则此三角形的周长为( ).
A.12 B.7+ C.12或7+ D.以上都不对
3. 等腰三角形的腰长为10,底长为12,则其底边上的高为( )
A.13 B.8 C.25 D.64
4. 如果一个直角三角形的两条直角边分别为n2﹣1,2n(n>1),那么它的斜边长是( )
A.2n B.n+1 C.n2﹣1 D.n2+1
5. 已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25 B.7 C.5和7 D.25或7
6. 将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是( ).
A.h≤17cm B.h≥8cm
C.15cm≤h≤16cm D.7cm≤h≤16cm
7. 如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8cm2 C.10cm2 D.12cm2
二、填空题
8. 在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2= .
9. 如图,△ABC中,AC=6,AB=BC=5,则BC边上的高AD=______.
10. 如图,四边形ABCD是正方形,AE垂直于BE,且AE=3,BE=4,阴影部分的面积是 .
11. 直角三角形的三边长为连续偶数,则其周长为 cm.
12. 如图,△ABC中,∠C=90°,AB垂直平分线交BC于D.若BC=8,AD=5,则AC等于 .
三、解答题
13. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和是多少?
14. 如图所示,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5 cm,求AB的长.
15. 去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2.732km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?(≈1.732)
答案:
1. C
分析:根据勾股定理先求出直角边的长度,再根据长方形的面积公式求出带阴影的矩形面积.
解:∵ =15厘米,
∴带阴影的矩形面积=15×3=45平方厘米.故选C.
2.C
(提示:因直角三角形的斜边不明确,结合勾股定理可求得第三边的长为5或,所以直角三角形的周长为3+4+5=12或3+4+=7+)
故选C;
3. B
分析:先作底边上的高,由等腰三角形的性质和勾股定理即可求出此高的长度.
解:作底边上的高并设此高的长度为x,根据勾股定理得:62+x2=102,
解得:x=8.故选B.
4. D
分析:根据勾股定理直接解答即可.
解:两条直角边与斜边满足勾股定理,则斜边长是: ===n2+1.故选D.
5. D
分析:分两种情况:①当3和4为直角边长时;②4为斜边长时;由勾股定理求出第三边长的平方即可.
解:分两种情况:
①当3和4为直角边长时,
由勾股定理得:第三边长的平方,即斜边长的平方=32+42=25;
②4为斜边长时,
由勾股定理得:第三边长的平方=42﹣32=7;
综上所述:第三边长的平方是25或7;故选:D.
6. D
(提示:筷子在杯中的最大长度为=17cm,最短长度为8cm,则筷子露在杯子外面的长度为24-17≤h≤24-8,即7cm≤h≤16cm,)
故选D.
7. A
分析:首先根据翻折的性质得到ED=BE,再设出未知数,分别表示出线段AE,ED,BE的长度,然后在Rt△ABE中利用勾股定理求出AE的长度,进而求出AE的长度,就可以利用面积公式求得△ABE的面积了.
解:∵长方形折叠,使点B与点D重合,
∴ED=BE,
设AE=xcm,则ED=BE=(9﹣x)cm,
在Rt△ABE中,
AB2+AE2=BE2,
∴32+x2=(9﹣x)2,
解得:x=4,
∴△ABE的面积为:3×4×=6(cm2).故选:A.
8.分析:由三角形ABC为直角三角形,利用勾股定理根据斜边AB的长,可得出AB的平方及两直角边的平方和,然后将所求式子的后两项结合,将各自的值代入即可求出值.
解:∵△ABC为直角三角形,AB为斜边,
∴AC2+BC2=AB2,又AB=2,
∴AC2+BC2=AB2=4,
则AB2+BC2+CA2=AB2+(BC2+CA2)=4+4=8.
故答案为:8
9. 3.6(提示:设DC=x,则BD=5-x.在Rt△ABD中,AD2=52-(5-x)2,在Rt△ADC中,AD2=62-x2,∴52-(5-x)2=62-x2,x=3.6.故AD==4.8);
10. 分析:在直角三角形ABE中,由AE与BE的长,利用勾股定理求出AB的长,由正方形面积减去直角三角形面积求出阴影部分面积即可.
解:∵AE⊥BE,∴∠AEB=90°,
在Rt△ABE中,AE=3,BE=4,
根据勾股定理得:AB==5,
则S阴影=S正方形﹣S△ABE=52﹣×3×4=25﹣6=19,
故答案为:19.
11.分析:设直角三角形的三边边长分别为2n﹣2,2n,2n+2,由勾股定理得:两直角边的平方和等于斜边的平方,据此列出关于n的方程,求出符合题意n的值,即求出了直角三角形的三边长,之后求出周长即可.
解:设直角三角形的三边边长分别为2n﹣2,2n,2n+2.由勾股定理得:
(2n﹣2)2+(2n)2=(2n+2)2,
解得:n1=4,n2=0(不合题意舍去),
即:该直角三角形的三边边长分别为6cm,8cm,10cm.
所以,其周长为6+8+10=24cm.
12.
分析:根据线段垂直平分线的性质可求得BD的长,从而求得CD的长,再根据勾股定理即可求得AC的长.
解:∵AB垂直平分线交BC于D,AD=5,
∴BD=AD=5,
∵BC=8,
∴CD=BC﹣BD=3,
∴AC==4,
故答案是:4.
13.
分析:根据正方形的面积公式,连续运用勾股定理,发现:四个小正方形的面积和等于最大正方形的面积.
解:由图形可知四个小正方形的面积和等于最大正方形的面积,
故正方形A,B,C,D的面积之和=49cm2.
故答案为:49cm2.
14.
解:.∵在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,
∴∠ABD=∠CBD=30°.
∴AD=DB.
又∵Rt△CBD中,CD=5 cm,
∴BD=10 cm.
∴BC===5(cm).
∴AB=2BC=10 cm.
15. 解 如图所示,过点C作CD⊥AB,垂足为点D,
由题意可得∠CAB=30°,∠CBA=45°,在Rt△CDB中,∠BCD=45°,∴∠CBA=∠BCD,∴BD=CD.在Rt△ACD中,∠CAB=30°,∴AC=2CD.设CD=DB=x,∴AC=2x.由勾股定理
得AD===x.∵AD+DB=2.732,
∴x+x=2.732,∴x≈1.即CD≈1>0.7,
∴计划修筑的这条公路不会穿过公园.
数学八年级下册1.2 直角三角形的性质与判定(Ⅱ)优秀课件ppt: 这是一份数学八年级下册1.2 直角三角形的性质与判定(Ⅱ)优秀课件ppt,文件包含教学课件八下·湘教·12直角三角形的性质和判定Ⅱ第3课时勾股定理的逆定理pptx、12直角三角形的性质和判定Ⅱ第3课时同步练习docx、12直角三角形的性质和判定Ⅱ第3课时教案docx等3份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
初中湘教版1.2 直角三角形的性质与判定(Ⅱ)获奖ppt课件: 这是一份初中湘教版1.2 直角三角形的性质与判定(Ⅱ)获奖ppt课件,文件包含教学课件八下·湘教·12直角三角形的性质和判定Ⅱ第2课时勾股定理的实际应用pptx、12直角三角形的性质和判定Ⅱ第2课时教案docx、12直角三角形的性质和判定Ⅱ第2课时同步练习docx等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中数学湘教版八年级下册1.2 直角三角形的性质与判定(Ⅱ)一等奖课件ppt: 这是一份初中数学湘教版八年级下册1.2 直角三角形的性质与判定(Ⅱ)一等奖课件ppt,文件包含教学课件八下·湘教·12直角三角形的性质和判定Ⅱ第1课时勾股定理pptx、12直角三角形的性质和判定Ⅱ第1课时教案docx、12直角三角形的性质和判定Ⅱ第1课时同步练习docx等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。













