初中数学湘教版八年级下册1.2 直角三角形的性质与判定（Ⅱ）复习练习题

[勾股定理的应用]

一、选择题

1.(2020永州祁阳县文昌中学期中)现在人们锻炼身体的意识日渐增强,但是一些人保护环境的意识却很淡薄,如图是兴庆公园的一角,有人为了抄近道而避开横平竖直的路的拐角∠ABC而走“捷径AC”,于是在草坪内走出了一条不该有的“路AC”.已知AB=40米,BC=30米,他们踩坏了　　　　米的草坪,只为少走　　　　米的路              (　　) 

A.20,50 B.50,20 C.20,30 D.30,20

2.《九章算术》中有一道“折竹抵地”的问题:今有竹高一丈,末折抵地,去根六尺.问折高者几何.意思是:一根竹子,原高一丈(1丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,则折断处离地面的高度是              (　　)

A.2.4尺 B.3尺 C.3.2尺 D.3.6尺

3.(教材“动脑筋”变式)一云梯AB长25米,如图斜靠在一面墙上,云梯底端离墙7米,如果云梯的顶端下滑了4米,那么它的底端在水平方向滑动的距离BB'的长是(　　)

A.10米 B.8米 C.6米 D.4米

4.(2021益阳南县期中)如图,在高为5 m,坡面长为13 m的楼梯表面铺地毯,地毯的长度至少需要              (　　)

A.17 m B.18 m C.25 m D.26 m

二、填空题

5.在两条垂直相交的道路上,一辆自行车和一辆摩托车相遇后又分别向北、向东驶去.若自行车与摩托车每秒分别行驶7.5米、10米,则相遇10秒后两车相距　　　　米. 

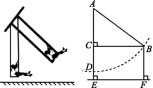
6.图是矗立在高速公路水平地面上的交通警示牌的示意图(M,A,B在同一条水平直线上),经测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则警示牌的高CD为　　　　米(结果精确到0.1米). 

7.(2021张家界期中)如图,长为8 cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3 cm到点D处,则橡皮筋被拉长了　　　　cm. 

三、解答题

8.如图,有一架秋千,当它静止时,踏板离地的垂直高度DE=1 m,将它往前推送6 m(水平距离BC=6 m)时,秋千的踏板离地的垂直高度BF=4 m,秋千的绳索始终拉得很直,求绳索AD的长度.

9.如图,在一棵树的10米高的B处有两只猴子.一只猴子爬下树走到离树20米远的池塘A处.另一只爬到树顶D后直接跃到A处.若两只猴子所经过的距离相等(距离以直线计算),则这棵树高多少米?

图   

10.近日A市气象局测得沙尘中心在A市正西方向450千米的B处,正以15千米/时的速度向南偏东60°的BF方向移动(如图),距离沙尘中心300千米的范围内是受沙尘暴严重影响的区域.

(1)通过计算说明A市必然会受到这次沙尘暴的严重影响;

(2)计算A市受沙尘暴严重影响的时间.

图   

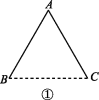
 [方案设计与优化问题] 由于湘中地区水资源缺乏,B,C两地不得不从资江上的扬水站A处引水,这就需要在A,B,C之间铺设地下输水管道.有人设计了3种铺设方案(图中实线表示管道铺设线路).在图②中,AD⊥BC于点D,且BD=DC;在图③中,OA=OB=OC,且AO的延长线交BC于点E,AE⊥BC,BE=EC,OE=OB.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短.若△ABC恰好是一个边长为a的等边三角形,请你通过计算,判断哪一种铺设方案最好.

图                 

答案

1.B

2. C　画出示意图如图所示.

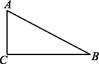
设折断处离地面的高度AC为x尺,则AB=(10-x)尺.由题意,得BC=6尺.

在Rt△ABC中,AC2+BC2=AB2,

即x2+62=(10-x)2,解得x=3.2,

即折断处离地面的高度是3.2尺.

3.B

4. A　由勾股定理,得楼梯的水平宽度为=12(m).∵地毯铺满楼梯的长度应该是楼梯的水平宽度与垂直高度的和,∴地毯的长度至少是12+5=17(m).

5.125

6. 2.9

 由题意,可知∠CMA=90°.

∵AM=4米,∠MAD=45°,∴DM=4米.

∵AM=4米,AB=8米,∴MB=12米.

∵在Rt△MBC中,∠MBC=30°,

∴BC=2MC,∴MC2+MB2=(2MC)2,

即MC2+122=(2MC)2,

∴MC=4米,则DC=4-4≈2.9(米).

7. 2

 由题意可知,在Rt△ACD中,AC=AB=4 cm,CD=3 cm,根据勾股定理,得AD==5 cm,∴AD+BD-AB=2AD-AB=10-8=2(cm),故橡皮筋被拉长了2 cm.

8.解:由题意,得CE=BF=4 m,

∴CD=CE-DE=4-1=3(m).

设秋千的绳索长为x m,则AC=(x-3)m,

在Rt△ACB中,AB2=BC2+AC2,

故x2=62+(x-3)2,解得x=7.5,

答:绳索AD的长度是7.5 m.

9.解:设树的高度为x米.两只猴子所经过的距离相等,都为30米.由勾股定理得x2+202=[30-(x-10)]2,解得x=15.故这棵树高15米.

10.解:(1)过点A作AD⊥BF于点D.

在Rt△ABD中,AB=450千米,∠ABD=30°,

∴AD=AB=×450=225(千米).

∵225千米<300千米,

∴A市必然会受到这次沙尘暴的严重影响.

(2)设沙尘中心距A市300千米时,刚好处在BF上的E,G两点,则DG=DE.

在Rt△ADE中,∵AE=300千米,AD=225千米,∴DE==75千米,

∴EG=2DE=150千米,

∴A市受沙尘暴严重影响的时间为=(时).

[素养提升]

解:题图①中,管道长为2a;

题图②中,AD===a,则管道长为a+a;

题图③中,设OE=x,则OB为2x,

在Rt△OBE中,由勾股定理,得

(2x)2-x2=a2,

解得x=a,

则OB=a,管道长为a×3=a.

∵2a>a+a>a,

∴题图③的铺设方案最好.