湘教版数学八年级下册同步练习 1.1 ~1.2滚动训练

B[范围:1.1 ~1.2]

一、选择题

1.在△ABC中,∠C=90°,∠A=15°,则∠B的度数为 (　　)

A.15° B.30° C.75° D.85°

2.(2021株洲南雅实验中学期中)如图,在Rt△ABC中,∠ACB=90°,AB=10,D是AB的中点,则CD的长为              (　　)

A.5 B.6 C.8 D.10

3.以下列四组数中的三个数为边长,不能构成直角三角形的是 (　　)

A.1,, B.5,12,13 C.32,42,52 D.8,15,17

4.如图,在△ABC中,AB=AC=10,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的平分线,DF∥AB交AE的延长线于点F,则DF的长是(　　)

A.2 B.4 C.5 D.

5.一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则该三角形的面积为 (　　)

A.8 B.10 C.24 D.48

6.图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果EF=4,AH=12,那么AB的长为              (　　)

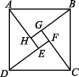
A.30 B.25 C.20 D.15

7.如图,在Rt△ABC和Rt△ABD中,∠ACB=∠ADB=90°,AB=10,M是AB的中点,连接MC,MD,CD,若CD=6,则△MCD的面积为              (　　)

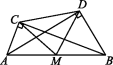
A.12 B.12.5 C.15 D.24

二、填空题

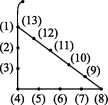
8.在没有直角工具之前,聪明的古埃及人用如图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中5个结间距长的边所对的角便是直角,依据是       　. 

9.已知在Rt△ABC中,∠C=90°,若a+b=14 cm,c=12 cm,则Rt△ABC的面积为　　　　. 

10.在△ABC中,高AD,BE所在的直线相交于点H,且BH=AC,则∠ABC=　. 

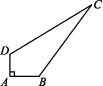
11.如图,在四边形ABCD中,AD=3,AB=4,BC=12,CD=13,∠A=90°,则四边形ABCD的面积为　　　　. 

12.如图所示,在△ABC中,∠C=2∠B,D是BC上一点,AD=5,且AD⊥AB,E是BD上一点,AE=BD,AC=6.5,则AB的长度为　　　　. 

三、解答题

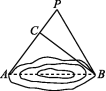
13.(2020耒阳冠湘中学期中)星期天,爱动脑筋的小刚同学用下面的方法测量家门前池塘两端A,B间的距离.他是这样做的:

如图,选定一个点P,连接PA,PB,在PA上取一点C,恰好有PA=14 m,PB=13 m,PC=5 m,BC=12 m,他立即确定池塘两端A,B间的距离为15 m.

小刚同学得出的结果正确吗?为什么?

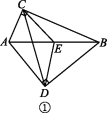
14.如图,已知AC⊥BC,AD⊥BD,E为AB的中点.

(1)如图①,求证:△ECD是等腰三角形;

(2)如图②,CD与AB交于点F,若AD=BD,EF=3,DE=4,求CD的长.

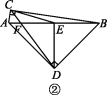
15.如图,在△ABC中,∠C=30°,∠BAC=105°,AD⊥BC,垂足为D,AC=2,求BC的长.

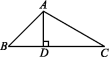
图   

16.如图所示,等腰三角形ABC的底边BC为8 cm,腰长为5 cm,一动点P在底边上从点B向点C以0.25 cm/s的速度移动.请你探究:当点P运动几秒时,点P与顶点A的连线PA与等腰三角形ABC的腰垂直?

答案

1.C　2.A

3. C　A选项,12+()2=()2,能构成直角三角形,故本选项不符合题意;

B选项,52+122=132,能构成直角三角形,故本选项不符合题意;

C选项,(32)2+(42)2≠(52)2,不能构成直角三角形,故本选项符合题意;

D选项,82+152=172,能构成直角三角形,故本选项不符合题意.

故选C.

4. C　∵AB=AC,AD是△ABC的中线,∴AD⊥BC,∠BAD=∠CAD=∠BAC=×120°=60°.∵AE是∠BAD的平分线,∴∠DAE=∠BAE.∵DF∥AB,∴∠F=∠BAE,∴∠DAE=∠F,∴AD=DF.

∵∠B=90°-60°=30°,∴AD=AB=×10=5,∴DF=5.

5. C　设另一直角边长为x,则斜边长为x+2.由勾股定理,得x2+62=(x+2)2,解得x=8,∴该三角形的面积=×6×8=24.

6. C　∵△ABH≌△BCG,∴BG=AH=12.

∵四边形EFGH是正方形,∴HG=EF=4,∴BH=16.

在Rt△ABH中,由勾股定理,得AB===20.

7. A　如图,过点M作ME⊥CD于点E.

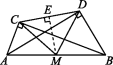
∵∠ACB=∠ADB=90°,AB=10,M是AB的中点,

∴CM=AB=5,DM=AB=5,∴CM=DM.

∵ME⊥CD,CD=6,∴CE=DE=3.

由勾股定理,得EM===4,∴△MCD的面积为CD·EM=×6×4=12.

8.如果三角形的三条边长a,b,c满足关系:a2+b2=c2,那么这个三角形是直角三角形

9. 13 cm2

 ∵∠C=90°,∴a2+b2=c2=144,

∴(a+b)2-2ab=144,

∴196-2ab=144,∴ab=26,

∴S△ABC=ab=13 cm2.

10. 45°或135°

 如图①,若∠ABC为锐角,

∵∠BHD=∠AHE,∠AEH=∠ADC=90°,

∴∠HBD+∠BHD=90°,∠AHE+∠HAE=90°,∴∠HBD=∠HAE.

在△HBD和△CAD中,

∵∠HBD=∠CAD,∠BDH=∠ADC,BH=AC,∴△HBD≌△CAD(AAS),∴AD=BD,

∴∠ABC=45°.

图①

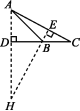
图②

如图②,若∠ABC是钝角,同理可得AD=BD,∴∠ABD=45°,∴∠ABC=135°.

综上所述,∠ABC的度数为45°或135°.

11. 36

 连接BD.在△ABD中,∵∠A=90°,AD=3,AB=4,

∴BD==5,

S△ABD=AB·AD=×4×3=6.

在△BCD中,∵BC=12,CD=13,BD=5,

∴BD2+BC2=CD2,

∴△BCD是直角三角形,且∠CBD=90°,

∴S△BCD=BC·BD=×12×5=30,

∴四边形ABCD的面积=S△ABD+S△BCD=6+30=36.

故答案为36.

12. 12

 在Rt△ABD中,∵AE=BD,

∴E是BD的中点,∴AE=BE=DE,

∴∠B=∠BAE,即∠AED=2∠B.

∵∠C=2∠B,∴∠AEC=∠C,

即AE=AC=6.5,

∴BD=2AE=13.

在Rt△ABD中,由勾股定理,得AB==12.

13.解:小刚同学得出的结果正确.理由如下:∵PA=14 m,PB=13 m,PC=5 m,BC=12 m,

∴AC=PA-PC=9(m),PC2+BC2=52+122=169,PB2=132=169,

∴PC2+BC2=PB2,

∴△BCP是直角三角形,∠BCP=90°,

∴∠ACB=90°,

∴AB===15(m).

即小刚同学得出的结果正确.

14.解:(1)证明:∵AC⊥BC,AD⊥BD,

∴∠ACB=90°,∠ADB=90°.

又∵E为AB的中点,

∴CE=AB,DE=AB,

∴CE=DE,∴△ECD是等腰三角形.

(2)∵AD=BD,E为AB的中点,

∴DE⊥AB.

∵DE=4,EF=3,

∴DF=5.

过点E作EH⊥CD于点H.

∵∠FED=90°,EH⊥DF,

∴EH==,

∴DH==.

同(1)得CE=DE,又EH⊥CD,

∴CD=2DH=.

15.解:∵AD⊥BC,∴∠ADB=∠ADC=90°.∵∠C=30°,AC=2,

∴∠CAD=60°,AD=AC=1,

∴CD===.

∵∠BAC=105°,

∴∠BAD=105°-60°=45°,

∴∠B=90°-45°=45°,∴BD=AD=1,

∴BC=BD+CD=1+.

16.解:如图,作AD⊥BC于点D.

∵AB=AC,BC=8 cm,

∴BD=CD=BC=4 cm,

∴AD=3 cm.

分两种情况:①设点P运动x s后,有PA⊥AC,如图(a).

∵AP2=PD2+AD2=PC2-AC2,

∴PD2+AD2=PC2-AC2,

即PD2+32=(PD+4)2-52,

∴PD=2.25 cm,

∴BP=BD-PD=4-2.25=1.75(cm),

即0.25x=1.75,∴x=7.

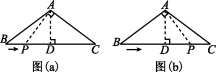
②设点P运动y s后,有PA⊥AB,如图(b),同理可求得PD=2.25 cm,

∴BP=BD+PD=4+2.25=6.25(cm),

即0.25y=6.25,∴y=25.

综上所述,当点P运动7 s或25 s时,点P与顶点A的连线PA与等腰三角形ABC的腰垂直.