


初中数学2.1 一元二次方程精品习题
展开2.1 一元二次方程
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题8分)
1.下列方程中是一元二次方程的是( )
A.xy+2=1 B.![]() C.x2=0 D.ax2+bx+c=0
C.x2=0 D.ax2+bx+c=0
2.一元二次方程3x2﹣3x=x+2化为一般形式ax2+bx+c=0后,a、b、c的值分别是( )
A.3、﹣4、﹣2 B.3、﹣3、2
C.3、﹣2、2 D.3、﹣4、2
3.关于x的方程(a﹣1)x|a|+1﹣3x+2=0是一元二次方程,则( )
A.a≠±1 B.a=1 C.a=﹣1 D.a=±1
4.若关于x的一元二次方程(m﹣2)x2+3x+m2﹣3m+2=0的常数项为0,则m等于( )
A.0 B.1 C.2 D.1或2
5.如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )
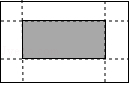
A.10×6﹣4×6x=32 B.(10﹣2x)(6﹣2x)=32
C.(10﹣x)(6﹣x)=32 D.10×6﹣4x2=32
二.填空题(共5小题,每题8分)
6.把下列方程中一元二次方程的序号填在横线上: .
①x2=4;②2x2+y=5 ;③![]() x+x2﹣1=0 ;④5x2=0 ;⑤3x2+
x+x2﹣1=0 ;④5x2=0 ;⑤3x2+![]() +5=0;⑥3x3﹣4x2+1=0.
+5=0;⑥3x3﹣4x2+1=0.
7.把一元二次方程(x+1)(1﹣x)=2x化成二次项系数大于零的一般式是 ,其中二次项系数是 ,一次项的系数是 ,常数项是 ;
8.当m= 时,关于x的方程(m﹣2)![]() +2x﹣1=0是一元二次方程.
+2x﹣1=0是一元二次方程.
9.某商品的原价为120元,如果经过两次降价,且每次降价的百分率都是m,那么该商品现在的价格是 元(结果用含m的代数式表示).
10.如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2,设小道进出口的宽度为x m,根据条件,可列出方程: .
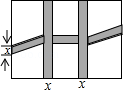
三.解答题(共3小题,第12、13题各7分,第11题6分)
11.试说明关于x的方程(a2﹣8a+20)x2+2ax+1=0无论a取何值,该方程都是一元二次方程.
12.关于x的一元二次方程(m+1)x2+5x+m2+3m+2=0的常数项为0,求m的值.
13.为了绿化学校附近的荒山,某校初三年级学生连续三年春季上山植树,至今已成活了2000棵,已知这些学生在初一时种了400棵,若平均成活率95%,求这个年级两年来植树数的年平均增长率.(只列式不计算)
试题解析
一.选择题
1.C
【分析】根据一元二次方程的定义:含有一个未知数,并且所含未知数的项的次数是2次的整式方程,即可判断答案.
【解答】解:根据一元二次方程的定义:A、是二元二次方程,故本选项错误;
B、是分式方程,不是整式方程,故本选项错误;
C、是一元二次方程,故本选项正确;
D、当a b c是常数,a≠0时,方程才是一元二次方程,故本选项错误;
故选:C.
【点评】本题考查了对一元二次方程和一元一次方程的理解,关键是知道一元二次方程含有3个条件:①整式方程,②含有一个未知数,③所含未知数的项的次数是1次.
2.A
【分析】直接利用移项、合并同类项,即可得出a,b,c的值.
【解答】解:一元二次方程3x2﹣3x=x+2化为一般形式ax2+bx+c=0后,
3x2﹣4x﹣2=0,
则a=3,b=﹣4,c=﹣2.
故选:A.
【点评】此题主要考查了一元二次方程的一般形式,正确合并同类项是解题关键.
3.C
【分析】根据一元一次方程的定义即可求出答案.
【解答】解:由题意可知:![]()
∴a=﹣1
故选:C.
【点评】本题考查一元二次方程的定义,解题的关键是熟练运用一元二次方程的定义,本题属于基础题型.
4.B
【分析】直接利用一元二次方程的定义以及结合一元二次方程的解法计算得出答案.
【解答】解:∵关于x的一元二次方程(m﹣2)x2+3x+m2﹣3m+2=0的常数项为0,
∴m2﹣3m+2=0,m﹣2≠0,
解得:m=1.
故选:B.
【点评】此题主要考查了一元二次方程的定义以及结合一元二次方程的解法,正确把握相关定义是解题关键.
5.B
【分析】设剪去的小正方形边长是xcm,则纸盒底面的长为(10﹣2x)cm,宽为(6﹣2x)cm,根据长方形的面积公式结合纸盒的底面(图中阴影部分)面积是32cm2,即可得出关于x的一元二次方程,此题得解.
【解答】解:设剪去的小正方形边长是xcm,则纸盒底面的长为(10﹣2x)cm,宽为(6﹣2x)cm,
根据题意得:(10﹣2x)(6﹣2x)=32.
故选:B.
【点评】本题考查由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.
二.填空题
6.①③④⑤
【分析】根据一元二次方程的定义:未知数的最高次数是2;二次项系数不为0选择正确的选项即可.
【解答】解:①x2=4是一元二次方程;
②2x2+y=5不是一元二次方程;
③![]() x+x2﹣1=0是一元二次方程;
x+x2﹣1=0是一元二次方程;
④5x2=0是一元二次方程;
⑤3x2+![]() +5=0是一元二次方程;
+5=0是一元二次方程;
⑥3x3﹣4x2+1=0不是一元二次方程;
是一元二次方程的有①③④⑤,
故答案为①③④⑤.
【点评】本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.
7.x2+2x﹣1=0,1,2,﹣1
【分析】通过去括号,移项,可以得到一元二次方程的一般形式,然后写出二次项系数,一次项系数和常数项.
【解答】解:去括号:1﹣x2=2x
移项:x2+2x﹣1=0
二次项系数是:1,一次项系数是:2,常数项是:﹣1.
故答案分别是:x2+2x﹣1=0,1,2,﹣1.
【点评】本题考查的是一元二次方程的一般形式,通过去括号,移项,可以得到一元二次方程的一般形式,然后写出二次项系数,一次项系数和常数项.
8.-2
【分析】根据一元二次方程的定义求得m的值,再进一步代入解方程即可.
【解答】解:根据一元二次方程的定义,得,
m2﹣2=2,且m﹣2≠0,
解得m=±2,且m≠2
m=﹣2.
故答案为:﹣2
【点评】此题主要是注意一元二次方程的条件:未知数的最高次数是二次,且系数不得为0.
9.120(1﹣m)2
【分析】设每次降价的百分率都是m,根据某商品的原价为120元,经过两次降价后的价格可用代数式表示出.
【解答】解:设每次降价的百分率都是m,
该商品现在的价格是;120(1﹣m)2.
故答案为:120(1﹣m)2.
【点评】本题考查理解题意的能力,知道原来的价格,知道降价的百分率,经过两次降价后可求出现在的价格,是个增长率问题.
10.x2﹣35x+34=0
【分析】设小道进出口的宽度为xm,根据矩形的面积以及平行四边形的面积结合种植花草的面积为532m2,即可列出关于x的一元二次方程,整理后即可得出结论.
【解答】解:设小道进出口的宽度为xm,
根据题意,得:30×20﹣20×2x﹣30x+2x•x=532,
整理,得:x2﹣35x+34=0.
故答案为:x2﹣35x+34=0.
【点评】本题考查了由实际问题抽象出一元二次方程,根据数量关系列出关于x的一元二次方程是解题的关键.
三.解答题
11.【分析】只要证明二次项系数不为零即可.
【解答】解:∵a2﹣8a+20=(a﹣4)2+4
又∵(a﹣4)2≥0,
∴a2﹣8a+20≠0,
∴关于x的方程(a2﹣8a+20)x2+2ax+1=0无论a取何值,该方程都是一元二次方程.
【点评】本题主要考查的是一元二次方程的定义,证得二次项系数不为零是解题的关键.
12.【分析】一元二次方程的一般形式是ax2+bx+c=0(a,b,c是常数且a≠0),a、b、c分别是二次项系数、一次项系数、常数项.
【解答】解:由题意,得
m2+3m+2=0,且m+1≠0,
解得m=﹣2,
m的值是﹣2.
【点评】本题考查了一元二次方程的一般形式:ax2+bx+c=0(a,b,c是常数且a≠0)特别要注意a≠0的条件.这是在做题过程中容易忽视的知识点.在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.
13.【分析】由题意可知三年来这些学生共植树:400+400(1+x)+400(1+x)2棵,已知成活率为:95%,所以成活了95%[400+400(1+x)+400(1+x)2]棵,又知成活了2000棵,令成活的棵数相等列出方程即可.
【解答】解:由题意得:初二时植树数为:400(1+x),
那么这些学生在初三时的植树数为:400(1+x)2;由题意得:
95%[400+400(1+x)+400(1+x)2]=2000.
【点评】本题主要考查一元二次方程的应用,关键在于已知平均增长率和原来的植树数,求两年后的植树数的方法.
湘教版九年级上册第2章 一元二次方程2.1 一元二次方程巩固练习: 这是一份湘教版九年级上册第2章 一元二次方程2.1 一元二次方程巩固练习,共5页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
初中数学湘教版九年级上册2.1 一元二次方程精品课后练习题: 这是一份初中数学湘教版九年级上册2.1 一元二次方程精品课后练习题,共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
数学九年级上册2.1 一元二次方程优秀同步训练题: 这是一份数学九年级上册2.1 一元二次方程优秀同步训练题,共4页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













