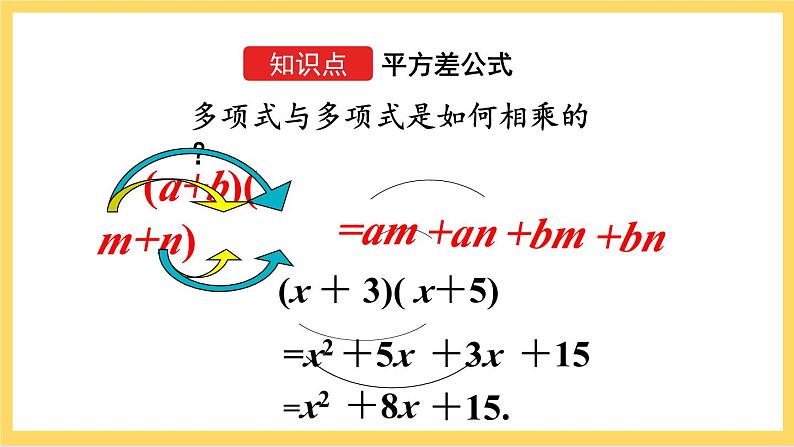
人教版八年级上册14.2.1 平方差公式精品ppt课件

第十四章  整式的乘法与因式分解

14.2 乘法公式

14.2.1 平方差公式

1. 下列运算中，可用平方差公式计算的是(　　)
A．(x＋y)(x＋y)                   B．(–x＋y)(x–y)
C．(–x–y)(y–x)                     D．(x＋y)(–x–y)

2. 计算(2x+1)(2x–1)等于(　　)
A．4x2–1      B．2x2–1      C．4x–1       D．4x2+1

3. 两个正方形的边长之和为5，边长之差为2，那么用较大的正方形的面积减去较小的正方形的面积，差是________．

4. 利用平方差公式计算：

(1)(a+3b)(a– 3b)；                (2)(3+2a)(–3+2a)；

(3)(–2x2–y)(–2x2+y).

5. 计算： 20152 – 2014×2016.

6. 利用平方差公式计算:

(1)(a–2)(a+2)(a2 + 4) ；         (2) (x–y)(x+y)(x2+y2)(x4+y4).

7. 先化简，再求值：(x+1)(x–1) +x2(1–x) +x3，其中x＝2.

8. 已知x≠1，计算：(1＋x)(1–x)＝1–x2，(1–x)(1＋x＋x2)＝1–x3，
(1–x)(1＋x＋x2＋x3)＝ 1–x4
(1)观察以上各式并猜想：(1–x)(1＋x＋x2＋…＋xn)＝________；(n为正整数)
(2)根据你的猜想计算：
①(1–2)(1＋2＋22＋23＋24＋25)＝________；
②2＋22＋23＋…＋2n＝________(n为正整数)；
③(x–1)(x99＋x98＋x97＋…＋x2＋x＋1)＝________；

参考答案：

1.C

2.A

3.10

4.解：（1）原式=(a)2–(3b)2
             =a2–9b2 ；

（2）原式=(2a+3)(2a–3)
         =(2a)2–32
         =4a2–9；

（3）原式=(–2x2 )2–y2
        =4x4–y2.
5. 解：20152 – 2014×2016
      = 20152 – (2015–1)(2015+1)
     = 20152– (20152–12 )
     = 20152–  20152+12
    =1

6.解：（1）原式=(a2–4)(a2+4)
              =a4–16.
（2）原式=(x2–y2)(x2+y2)(x4+y4)
          =(x4–y4)(x4+y4)

        =x8–y8.
7. 解：原式=x2–1＋x2–x3＋x3
          =2x2–1.

      将x＝2代入上式，

     原式=2×22–1=7.

8.（1）1–xn+1 ；（2）①-63；②2n＋1–2；③x100–1.