初中数学人教版八年级上册14.1.4 整式的乘法一等奖课件ppt

第十四章   整式的乘法与因式分解

14.1.4 整式的乘法

第2课时  多项式乘以多项式

一、教学目标

【知识与技能】

理解多项式乘以多项式的运算法则,能够按多项式乘法步骤进行简单的乘法运算.

【过程与方法】

经历探索多项式与多项式相乘的运算法则的推理过程,体会数学的转化思想.

【情感、态度与价值观】

通过推理,培养学生计算能力,发展有条理的思考,逐步形成主动探索的习惯.

二、课型

新授课

三、课时

第2课时

四、教学重难点

【教学重点】 

多项式与多项式相乘的法则的概括与运用.

【教学难点】

灵活运用法则进行计算和化简. 

五、课前准备 

教师：课件、直尺等。

学生：练习本、钢笔或圆珠笔。

六、教学过程

（一）导入新课

为了把校园建设成为花园式的学 校，经研究决定将原有的长为a米， 宽为b米的足球场向宿舍楼方向加长 m米，向厕所方向加宽n米，扩建成为美化校园绿草地.你是学校的小主人，你能帮助学校计算出扩展后绿地的面积吗？（出示课件2）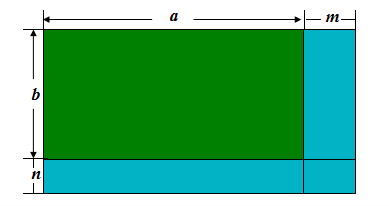

（二）探索新知

1.师生互动，探究多项式乘以多项式的法则

教师问1：请同学们完成下面的题目：

计算：(1)－2x2·3xy2；(2)－2x(1－x)；

(3)x(4x2＋x)；(4)(4x2－x－1)·9x.

学生回答：(1)－2x2·3xy2=-6x3y2；

(2)－2x(1－x)=-2x+2x2；

(3)x(4x2＋x)=4x3+x2；

(4)(4x2－x－1)·9x=36x3-4x2-9x.

教师问2：结合上题回忆单项式乘以单项式是什么？

学生回答：单项式与单项式相乘，把它们的系数、同底数幂分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式.

教师问3：单项式乘以多项式的法则是什么？

学生回答：单项式与多项式相乘，就是用单项式乘多项式的每一项，再把所得的积相加.（出示课件4）

教师问4：在计算x(4x2＋x)时，x代表一个单项式，如果x＝y＋2，则式子转化为(y＋2)(4x2＋x)，你能计算它的结果吗？

学生讨论后回答：首先把（y+2）看作一个整体进行计算得：

(y＋2)(4x2＋x)

=（y+2）4x2+(y+2)x

然后按单项式乘以多项式进行计算得：

(y＋2)(4x2＋x)

=（y+2）4x2+(y+2)x

=4x2y+8x2+xy+2x

教师问5：类比上题计算：(a＋b)(p＋q).

学生讨论后回答：将(a＋b)看做一个字母或将(p＋q)看做一个字母进行计算.

解法一：将(a＋b)看做一个字母计算得：

(a＋b)(p＋q)

=(a＋b)p+(a＋b)q

=ap+bp+aq+bq

解法二：将(p＋q)看做一个字母计算得：

(a＋b)(p＋q)

=a(p＋q)+b(p＋q)

=ap+aq+bp+bq

教师问6：再次观察：以上运算过程，从形式上说，这是什么运算？

学生回答：多项式乘以多项式的运算.

教师问7：多项式乘以多项式是怎么进行计算的？

学生回答：用一个多项式乘以另一个多项式.

教师问8：你能归纳多项式乘以多项式的法则吗？

学生小组讨论给出答案：多项式乘以多项式，先用一个多项式的每一项乘另一个多项式的每一项.

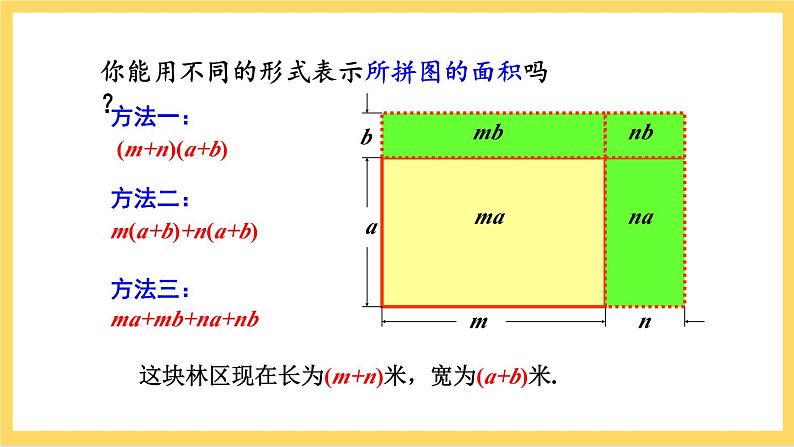
教师出示问题：某地区在退耕还林期间，有一块原长m米，宽为a米的长方形林区，若长增加了n米，宽增加了b米，请你计算这块林区现在的面积.（出示课件5）

教师问9：你能用不同的形式表示所拼图的面积吗？（出示课件6）

学生讨论后回答如下：

方法1：(m+n)(a+b)
方法2：m(a+b)+n(a+b)

方法3：(m＋n)a＋(m＋n)b

方法4：ma+mb+na+nb

教师问10：由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积，所以可以得到什么？（出示课件7）
学生回答：(m+n)(a+b)=ma+mb+na+nb.

教师问11：从以上过程你能否得出多项式乘以多项式的法则？你又有什么体会？

学生讨论后回答：实际上，把(a+b)看成一个整体，有：

(m+n)(a+b)

=m(a+b)+n(a+b)
= ma+mb+na+nb
总结点拨：（出示课件8）

多项式乘以多项式
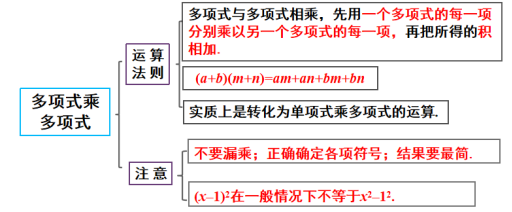
多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加.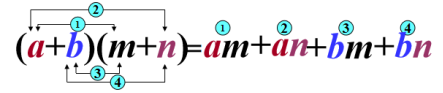

“多乘多” 顺口溜：

多乘多，来计算，多项式各项都见面，
乘后结果要相加，化简、排列才算完.
    例1：计算: (1)(3x+1)(x+2)；(2)(x–8y)(x–y)；(3) (x+y)(x2–xy+y2).
    师生共同解答如下：（出示课件9-10）

解： (1) 原式=3x·x+2·3x+1·x+1×2
            =3x2+6x+x+2
            =3x2+7x+2；

易错提醒：结果中有同类项的要合并同类项.

(2) 原式=x·x–xy–8xy+8y2
=x2–9xy+8y2；
易错提醒：计算时要注意符号问题.

(3) 原式=x·x2–x·xy+xy2+x2y–xy2+y·y2
        =x3–x2y+xy2+x2y–xy2+y3
        = x3+y3.
    易错提醒：计算时不能漏乘.

总结点拨：需要注意的几个问题：(1)漏乘；(2)符号问题；(3)最后结果应化成最简形式.
    例2：先化简，再求值：

(a–2b)(a2＋2ab＋4b2)–a(a–5b)(a＋3b)，其中a＝–1，b＝1.（出示课件12）

师生共同解答如下：

解：原式＝a3–8b3–(a2–5ab)(a＋3b)
＝a3–8b3–a3–3a2b＋5a2b＋15ab2
＝–8b3＋2a2b＋15ab2.
当a＝–1，b＝1时，
原式＝–8＋2–15＝–21.
例3：已知ax2＋bx＋1(a≠0)与3x–2的积不含x2项，也不含x项，求系数a、b的值．（出示课件14）
师生共同解答如下：

解：(ax2＋bx＋1)(3x–2)

＝3ax3–2ax2＋3bx2–2bx＋3x–2，

∵积不含x2的项，也不含x的项，

总结点拨：解决此类问题首先要利用多项式乘法法则计算出展开式，合并同类项后，再根据不含某一项，可得这一项系数等于零，再列出方程(组)解答．
  （三）课堂练习（出示课件18-26）

1. 计算(x–1)(x–2)的结果为(　　)
     A．x2+3x–2                                 B．x2–3x–2
     C．x2+3x+2                                 D．x2–3x+2
    2. 如果(x+a)(x+b)的结果中不含x的一次项，那么a、b满足(　　)
    A．a=b             B．a=0             C．a=–b          D．b=0

3. 已知ab=a+b+1，则(a–1)(b–1)=_____．

4. 判别下列解法是否正确，若不正确，请说出理由.
（1）（2x-3）(x-2)-(x-1)2 ;

解：原式=2x2-4x+6-(x-1)(x-1)

       =2x2-4x+6-(x2-2x+1)
      =2x2-4x+6-x2+2x-1

      =2x2-2x+5

（2）（2x-3）(x-2)-(x-1)2

解：原式=2x2-4x-3x+6-(x2-12)

       =2x2-7x+6-x2+1
           =x2-7x+7

5. 计算：(1)(x−3y)(x+7y)；      (2)(2x + 5y)(3x−2y).
6.化简求值：
(4x+3y)(4x–3y)+(2x+y)(3x–5y)，其中x=1，y= –2.
7. 解方程与不等式：
①(x–3)(x–2)+18=(x+9)(x+1)；②(3x+6)(3x–6)＜9(x–2)(x+3)．

8. 小东找来一张挂历画包数学课本．已知课本长a厘米，宽b厘米，厚c厘米，小东想将课本封面与封底的每一边都包进去m厘米，那么小东应在挂历画上裁下一块多大面积的长方形？

参考答案：

1.D

2.C

3.2

4.解：（1）解：原式=2x2-4x +6-(x-1)(x-1)   漏乘

       =2x2-4x+6-(x2-2x+1)
           =2x2-4x+6-x2+2x-1

       =2x2-2x+5

（2）解：原式=2x2-4x-3x+6-(x2-12)          运算法则混淆

       =2x2-7x+6-x2+1
           =x2-7x+7           

5. 解: (1) (x−3y)(x+7y)
=x2+7xy-3yx-21y2

   = x2 +4xy–21y2；

(2) (2x +5 y)(3x−2y)
= 2x•3x−2x• 2y+5 y• 3x- 5y•2y
=6x2-4xy+15xy-10y2

= 6x2 +11xy−10y2.
6. 解:原式=16x2-12xy+12xy-9y2+6x2-10xy+3xy-5y2

        =22x2-7xy-14y2

当x=1，y= –2时，
原式=22×1–7×1×(–2)–14×(–2)2
=22+14 –56
=–20.
7. 解：①原式去括号，得:x2–5x+6+18=x2+10x+9，
         移项合并，得:15x=15，
         解得:x=1；
        ②原式去括号，得:9x2–36＜9x2+9x–54，
         移项合并，得:9x＞18，
          解得:x＞2 ．
8.解：

面积：(2m+2b+c)(2m+a)
解：(2m+2b+c)(2m+a)
=  4m2+2ma+4bm+2ab+2cm+ca.
答：小东应在挂历画上裁下一块
(4m2+2ma+4bm+2ab+2cm+ca)平方厘米的长方形.
（四）课堂小结

今天我们学了哪些内容:

(1) 法则：多项式乘以多项式，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.

(2)在运用多项式与多项式相乘的法则时，你认为应该注意哪些问题？

(3)举例说明在探索多项式与多项式相乘的法则的过程中，体现了哪些思想方法？

（五）课前预习

预习下节课（14.1.4）102页到104页的相关内容。

知道同底数幂除法的法则、零指数幂的意义、单项式除以单项式的法则，单项式除以多项式的法则.

七、课后作业

1、教材102页练习1,2

2、为应对国际金融危机,我国出台了一系列刺激住房消费的优惠政策.李小雨家刚刚买了一套房子,房子的结构如图所示(单位:m),他家打算在房子里铺满地砖.

 (1)他家至少需要购买多少平方米的地砖?

(2)如果铺设的这种地砖的价格是每平方米3n元,请你帮他家算一算至少需要花多少钱?

八、板书设计：

九、教学反思：

1.本节的内容是多项式的乘法,针对本节课学生的易错点,如“漏项”、忘变号的情况,在例题后进行强调,并总结规律,让学生以后在练习计算时避免“漏项”、变号的发生.

2.在教学过程中，学生发现多项式与多项式相乘的法则，第一步是“转化”为多项式与单项式相乘，第二步则是“转化”为单项式乘法，那么，两次运用单项式与多项式相乘的法则，就得出多项式相乘的法则了.从而让学生进一步体会“转化”的思想方法：学习一种新的知识、方法，通常的做法是把它归结为已知的知识、方法，从而使学习能够进行.