第一章全等三角形小结-(苏科版) 课件PPT

这是一份第一章全等三角形小结-(苏科版) 课件PPT，共30页。

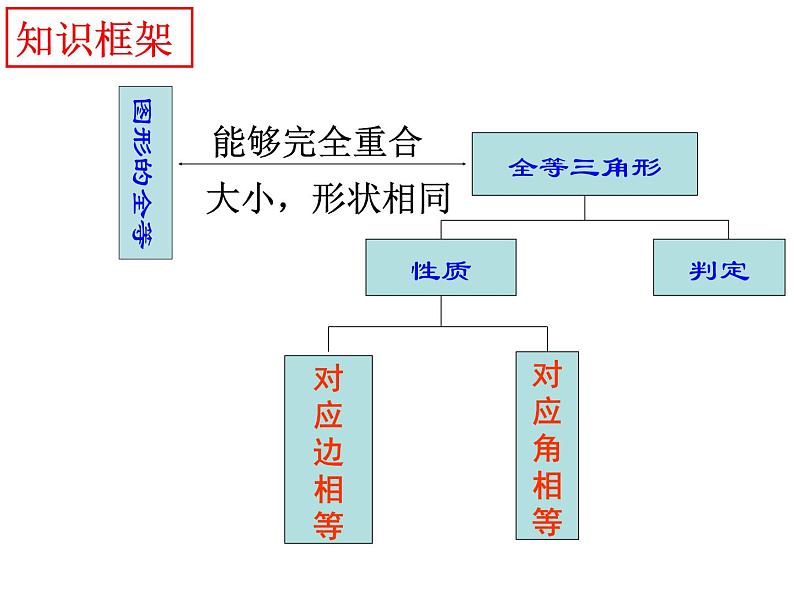
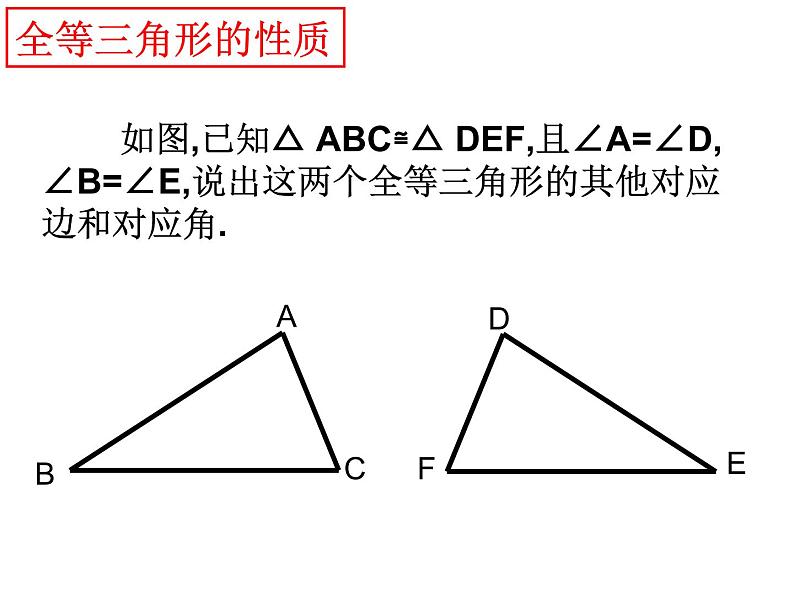
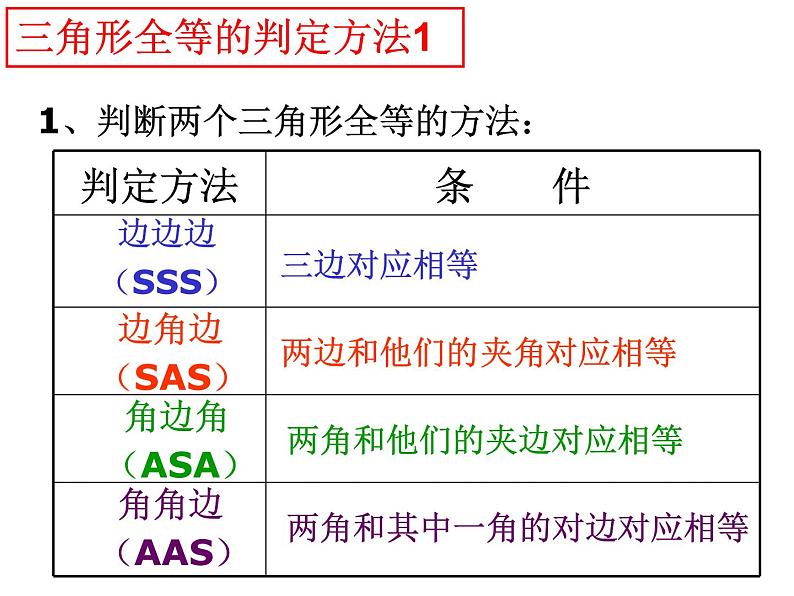
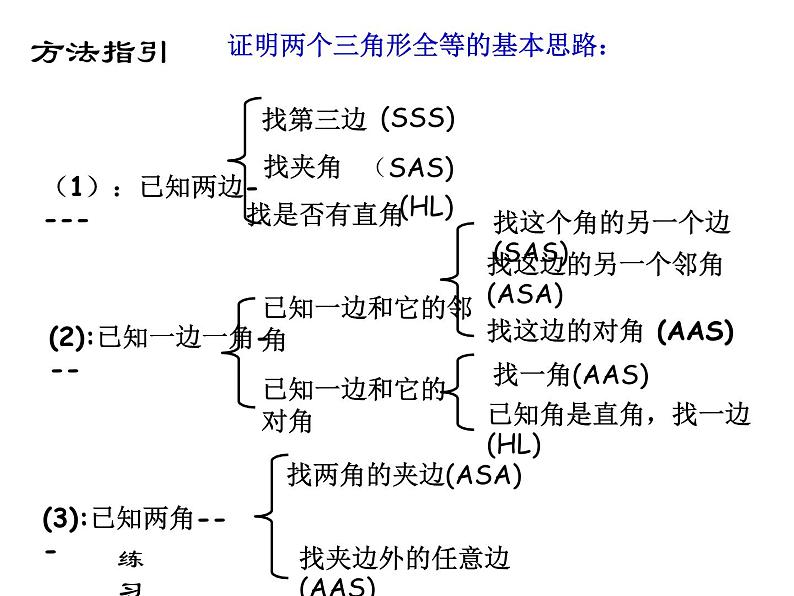
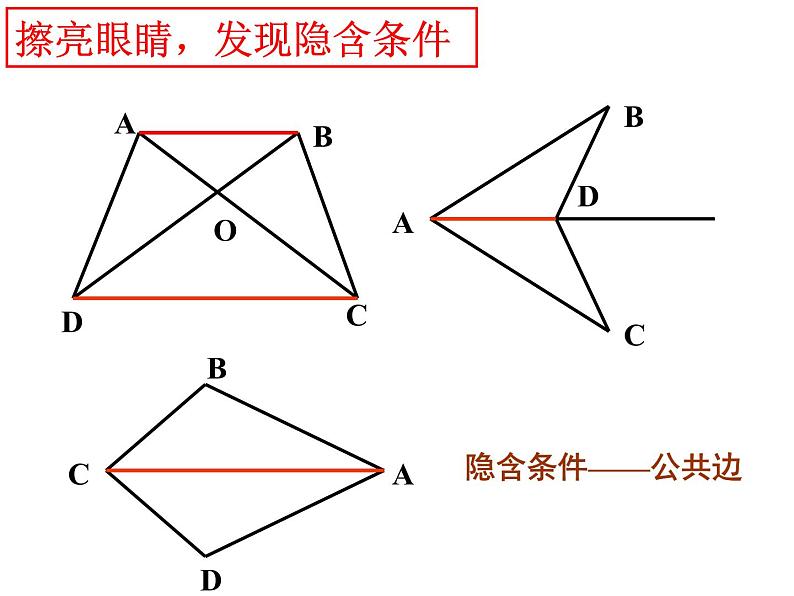
第一章全等三角形复习全等三角形性质判定对应边相等对应角相等能够完全重合大小，形状相同知识框架图形的全等CAB 如图,已知△ ABC≌△ DEF,且∠A=∠D, ∠B=∠E,说出这两个全等三角形的其他对应边和对应角.EDF全等三角形的性质1、判断两个三角形全等的方法：边边边（SSS）三边对应相等边角边（SAS）两边和他们的　　对应相等角边角（ASA）两角和他们的夹边对应相等角角边（AAS）两角和　　　　　　　对应相等夹角其中一角的对边三角形全等的判定方法12、判断两个直角三角形全等的方法：Ａ．一般三角形全等的判定方法对直角三角形全等的判定　　同样适用．Ｂ．斜边直角边（ＨＬ）斜边和一条直角边对应相等三角形全等的判定方法2方法指引证明两个三角形全等的基本思路：（1）：已知两边---- 找第三边(SSS)找夹角（SAS)(2):已知一边一角---已知一边和它的邻角找是否有直角(HL)已知一边和它的对角找这边的另一个邻角(ASA)找这个角的另一个边(SAS)找这边的对角 (AAS)找一角(AAS)已知角是直角，找一边(HL)(3):已知两角---找两角的夹边(ASA)找夹边外的任意边(AAS)练习认准对应边、对应点例1：在△ABC和△DEF中，已知∠C=∠D，∠B=∠E，要判定这两个三角形全等，还需要条件（ ）A.AB=EDB.AB=FDC.AC=FDD.∠A=∠F解决这类几何问题，一定要观察图形，没有图要画图擦亮眼睛，发现隐含条件ADCBADCBDBCAO隐含条件——公共边隐含条件——公共角隐含条件——对顶角擦亮眼睛，发现隐含条件1. 如图，已知AD=AC，要使△ADB≌△ACB，需要添加的一个条件是__________.找夹角找第三边找直角已知两组边：∠DAB=∠CAB （SAS）BD=BC （SSS）∠D=∠C=90°（HL）判定思路1BCDA2：如图，已知AD=AE，AB=AC。（1）求证：∠B=∠C；（2）若∠A=50o，问△ADC经过怎样的变换能与△AEB重合？判定思路1——变式训练2.如图，已知∠B=∠E，要识别△ABC≌△AED，需要添加的一个条件是 。已知两组角：找夹边找一角的对边AB=AEAC=AD或 BC=ED(ASA)(AAS)判定思路23.如图，已知AB=AE，要使△ABC≌△AED，需要添加的一个条件是__________。已知一组边一组角（边与角相邻）：找夹这个角的另一边找夹这条边的另一角找边的对角AC=AD∠B=∠E∠ACB=∠ADE（SAS）（ASA）（AAS）判定思路34.如图，已知BC=ED，要使△ABC≌△AED，需要添加的一个条件是__________。找任一角 已知一组边一组角（边与角相对）（AAS）∠B=∠E或者∠ACB=∠ADE判定思路4（AAS）4.如图，已知BC=ED，要使△ABC≌△AED，需要添加的一个条件是__________。找任一角（AAS）∠B=∠E或者∠ACB=∠ADE判定思路4（AAS）要防止出现“SSA”的错误！ 已知一组边一组角（边与角相对） 四个等式：① ，② ，③ ，④ 请从这四个等式中选出两个作为条件，推出是AE=DE．已知：求证：分类例题1——判定方法的选择 如图，点B、E、C、F在同一条直线上，AB＝DE，AC＝DF，BE＝CF， 试说明∠A＝∠DDBAEFC分类例题2——重叠线段 已知：如图，AD＝BC。请添加一个条件，使图中存在全等三角形并给予证明。（1）你所加条件为＿＿＿＿＿＿＿，（2）得到的一对全等三角形是 △＿＿＿≌△＿＿＿。（3）证明：分类例题2——重叠线段已知：如图，BA=BD，BC=BE，∠ABD=∠CBE：求证：AC=DE分类例题3——重叠角 如图，在等腰Rt△ABC中，P是斜边BC的重点，以P为顶点的直角的两边分别与边AB，AC交与点E，F，连接EF。当∠EPF绕顶点P旋转时，△PEF也始终是等腰直角三角形，请你说明理由。分类例题3——重叠角 例4：用直尺和圆规作一个角等于已知角的示意图如图所示，则说明 依据是 。分类例题4——全等的应用 1尺规作图作∠AOB的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D，再分别以点C、D 为圆心，以大于 长为半径画弧，两弧交于点P，作射线AP，由作法得 的根据是（ ）A．SAS B．ASA C．AAS　　D．SSS 分类例题4——全等的应用2.如图, 作△ABC的角平分线BM,CN相交于点P,作PE垂直BC于E点，PF垂直AC于F点，PD垂直AB于D点求证：PD=PE=PF拓展题1.如图,已知AC∥BD，EA、EB分别平分∠CAB和∠DBA，CD过点E，则AB与AC+BD相等吗？请说明理由。要证明两条线段的和与一条线段相等时常用的两种方法：1、可在长线段上截取与两条线段中一条相等的一段，然后证明剩余的线段与另一条线段相等。（割）2、把一个三角形移到另一位置，使两线段补成一条线段，再证明它与长线段相等。（补）2.如图：在四边形ABCD中，点E在边CD上，连接AE、BE并延长AE交BC的延长线于点F，给出下列5个关系式：：①AD∥BC，②，DE=EC③∠1=∠2，④∠3=∠4，⑤AD+BC=AB。将其中三个关系式作为已知，另外两个作为结论，构成正确的命题。请用序号写出两个正确的命题：（书写形式：如果……那么……）（1） ；（2） ；3.如图，在R△ABC中，∠ACB=45°，∠BAC=90°，AB=AC，点D是AB的中点，AF⊥CD于H交BC于F，BE∥AC交AF的延长线于E，求证：BC垂直且平分DE.4.已知：如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG。求证：△ ADG 为等腰直角三角形。5.已知：如图21，AD∠BAC，DE⊥AB于E，DF⊥AC于F，DB=DC，求证：EB=FC6.已知，△ABC和△ECD都是等边三角形，且点B，C，D在一条直线上求证：BE=AD 变式：以上条件不变，将△ABC绕点C旋转一定角度（大于零度而小于六十度），以上的结论海成立吗？方法小结证明两个三角形全等的基本思路：（1）：已知两边---- 找第三边(SSS)找夹角（SAS)(2):已知一边一角---已知一边和它的邻角找是否有直角(HL)已知一边和它的对角找这边的另一个邻角(ASA)找这个角的另一个边(SAS)找这边的对角 (AAS)找一角(AAS)已知角是直角，找一边(HL)(3):已知两角---找两角的夹边(ASA)找夹边外的任意边(AAS)练习