人教版九年级上册第二十一章 一元二次方程21.1 一元二次方程公开课复习ppt课件

这是一份人教版九年级上册第二十一章 一元二次方程21.1 一元二次方程公开课复习ppt课件，共43页。

1.梳理本章的知识结构网络，回顾与复习本章知识.2.能选择适当的方法，快速、准确地解一元二次方程，知道一元二次方程根的判别式和一元二次方程根与系数的关系，并能利用它们解决有关问题.3.列一元二次方程解决实际问题.（重、难点）4.进一步加深对方程思想、分类思想、转化思想（即降次）的理解与运用.
ax²+bx+c=0（a0）
二次项系数为1，而一次项系数为偶数
根的判别式Δ=b2−4ac
Δ>0,方程有两个不等的实数根Δ=0,方程有两个相等的实数根Δ<0,方程无实数根
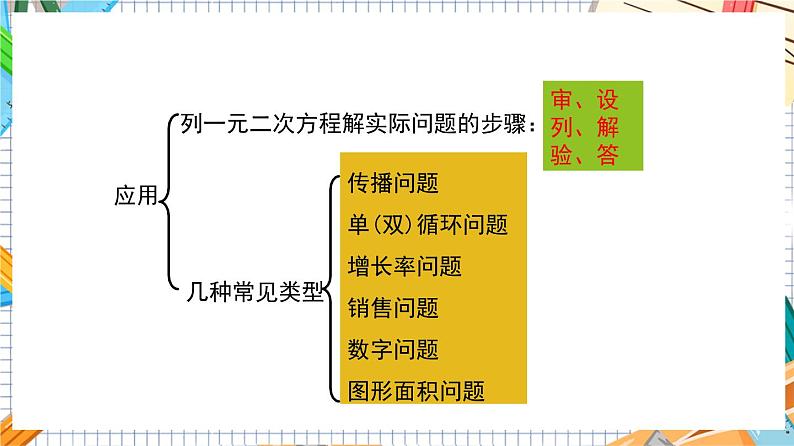
列一元二次方程解实际问题的步骤：
传播问题单(双)循环问题增长率问题销售问题数字问题图形面积问题
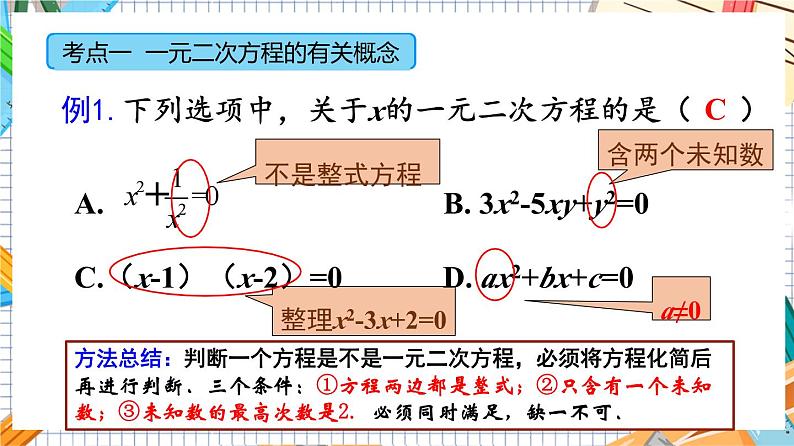
例1.下列选项中，关于x的一元二次方程的是（ ）
整理x2-3x+2=0
A. B. 3x2-5xy+y2=0C.（x-1）（x-2）=0 D. ax2+bx+c=0
方法总结：判断一个方程是不是一元二次方程，必须将方程化简后再进行判断．三个条件：①方程两边都是整式；②只含有一个未知数；③未知数的最高次数是2. 必须同时满足，缺一不可．
1 下列方程中，关于x的一元二次方程是（　　）A．x2−x（x+3）=0B．ax2+bx+c=0C．x2−2x−3=0 D．x2−2y −1=0
解析 A.将方程化简后，为一次方程；B.未限定二次项系数a不为0；D.含有两个未知数，只有C符合一元二次方程的定义，故选C.
2.方程5x2−x−3=x2−3+x的二次项系数是 ，一次项系数是 ，常数项是 .
解析 根据一元二次方程根的定义可知将x=0代入原方程一定会使方程左右两边相等，故只要把x=0代入就可以得到以m为未知数的方程m2−1=0，解得m=±1.这里应填−1.这种题的解题方法我们称之为“有根必代”.
例2 若关于x的一元二次方程(m−1)x2+x+m2−1=0有一个根为0，则m= .
【易错提示】求出m的值有两个，分别为1和−1，由于原方程是一元二次方程，所以1不符合，应引起注意.
2. （1）一元二次方程x2+px−2=0的一个根为2，则p的值为 .（2）若x=−2是方程ax2+bx+3=0（a≠0）的一个解，则代数式1−8a+4b的值是 ．（3）若x=a是方程x2−x−1=0的一个根，则−a3+2a+2020的值为_________.
解析 (1)配方法的关键是配上一次项系数一半的平方；(2)先求出方程x2﹣13x+36=0的两根，再根据三角形的三边关系，得到符合题意的边长，进而求得三角形周长．
例3 (1)用配方法解方程x2−2x−5=0时，原方程应变为（ ） A. (x−1)2=6 B.(x+2)2=9 C. (x+1)2=6 D.(x−2)2=9(2) (易错题）三角形两边长分别为3和6，第三边的长是方程x2﹣13x+36=0的根，则该三角形的周长为（　）　A.13 B.15 C.18 D.13或18
3.利用直接开平方法解下列方程:
∴x1=30, x2=－30.
4.解下列方程：（1）（x＋1）2= 2 ；
解析：本题中只要将（x＋1）看成是一个整体，就可以运用直接开平方法求解.
解：（1）∵x+1是2的平方根，
5.解下列方程：
6.解方程：(1)x2−4x −1=0 ;
(1)x2−4x−1=0 ;
(2)(2x−1)2=(3−x)2;
直接开方法：2x−1=±(3-x)，
即2x−1=3−x或2x−1=−3+x，
因式分解法：移项得(2x−1)2−(3−x)2=0.
分解因式，得(2x−1−3+x)(2x−1+3−x)=0.
即3x−4=0，或x+2=0.
拓展：(x2−2x)2−5x2+10x+6=0．
解：方程整理得(x2−2x)2−5(x2−2x)+6=0，
设x2−2x=m，则原方程变为m2−5m+6=0，
解得m1=3，m2=2，
当m=3时，x2−2x=3，解得x=3或−1，
例4.不解方程，判断下列方程根的情况：
解：a＝﹣1，b＝ ，c＝﹣6, △= b2-4ac =24－4×（﹣1）×（-6）=0. 该方程有两个相等的实数根.
解： 移项，得 x2+4x-2=0, a＝1，b＝4 ，c＝﹣2, △= b2-4ac =16-4×1×（-2）=24＞0.该方程有两个不相等的实数根.
（2）x2+4x=2;
【易错提示】应用根的判别式之前务必将方程化为一般形式，这样能帮助我们正确确定a，b，c的值.
8.下列所给方程中，没有实数根的是（ ）A. x2+x=0 B. 5x2−4x−1=0 C.3x2−4x+1=0 D. 4x2−5x+2=09.（开放题）若关于x的一元二次方程x2−x+m=0有两个不相等的实数根，则m的值可能是　　（写出一个即可）．
例5.利用根与系数的关系，求下列方程的两根之和、两根之积. （1）x2 + 7x + 6 = 0;
解：这里 a = 1 , b = 7 , c = 6. Δ = b2 - 4ac = 72 – 4 × 1 × 6 = 25 > 0.∴方程有两个实数根.设方程的两个实数根是 x1, x2, 那么x1 + x2 = -7 , x1 x2 = 6.
10. 已知一元二次方程x2－4x－3＝0的两根为m，n，则m2－mn＋n2＝ ．
解析：根据根与系数的关系可知，m+n=4，mn=−3. m2－mn＋n2＝m2+n2−mn=(m+n)2−3mn=42−3×(−3)=25.故填25.
解：(1)根据题意得Δ=(2m)2−4(m2+m)≥0，
(2)根据题意得x1+x2=−2m，x1x2=m2+m，
∴(−2m)2-2(m2+m)=12，
解得m1=−2，m2=3(不合题意，舍去)．
例6.电脑勒索病毒的传播非常快，如果开始有6台电脑被感染，经过两轮感染后共有2400台电脑被感染. 每轮感染中平均一台电脑会感染几台电脑？
解：设每轮感染中平均一台电脑会感染x台电脑.
答：每轮感染中平均一台电脑会感染19台电脑.
依题意得 6+6x+6x (1+x) =2400.
6 (1+x)² =2400
12.有一人患了流感，假如平均一个人传染了x个人，经过两轮感染后共有121人患了流感，依题意可列方程为 ．
1+x+x（1+x）=121
例7.一个小组若干人，新年互送贺卡，若全组共送贺卡72张，则这个小组共多少人？
设这个小组共x人，根据题意列方程，得
x(x-1)=72.
化简，得 x2-x-72=0.
解方程，得 x1=9， x2=-8（舍去）.
13. 某班同学毕业时，都将自己的照片向本班其他同学送一张留念，全班一共送了1260张，如果全班有x名同学，根据题意，列出方程为（　　）A．x(x+1)=1260 B．2x(x+1)=1260C．x(x−1)=1260×2 D．x(x−1)=1260
例8.某药品经两次降价，零售价降为原来的一半.已知两次降价的百分率一样，求每次降价的百分率.（精确到0.1%）
解：设原价为1个单位，每次降价的百分率为 x.根据题意，得 .
答：每次降价的百分率为29.3%.
某种药品原价为36元/盒，经过连续两次降价后售价为25元/盒.求平均每次降价的百分率？
解：设平均每次降价的百分率为x，根据题意得：
36（1- x ）2=25.
答：平均每次约降价16.7%.
14. 新冠肺炎疫情期间，某餐馆老板小王每日为一线抗疫医护人员免费提供3000份盒饭，各省医务人员纷纷驰援武汉之后，小王连续两次增加盒饭数量，每日提供5880份盒饭.求平均每次增加的盒饭数量的百分率.
解：设平均每次增加的盒饭数量的百分率是x，根据题意得 3000(1+x)2=5880 解得 x1=-2.4 (舍去)， x2=0.4=40%.答：平均每次增加的盒饭数量的百分率是40%.
例9 某机械公司经销一种零件，已知这种零件的成本为每件20元，调查发现当销售价为24元，平均每天能售出32件，而当销售价每上涨1元，平均每天就少售出2件.(1)若公司每天的销售价为x元，则每天的销售量为多少？(2)如果物价部门规定这种零件的销售价不得高于每件28元，该公司想要每天获得150元的销售利润，销售价应当为多少元？
解析：本题为销售中的利润问题，其基本数量关系用表析分如下：设公司每天的销售价为x元.
(x−20)[32−2(x−24)]
其等量关系：总利润=单件利润×销售量.
解：(1)32−(x−24) ×2=80−2x.
(2)由题意可得(x−20)(80−2x)=150.
【易错提示】根据实际情况及题目限制条件，对根进行取舍.
解得 x1=25， x2=35.
由题意x≤28，∴x=25，即售价应当为25元.
15.2020年，我国脱贫攻坚在力度、广度、深度和精准度上都达到了新的水平，重庆市深度贫困地区脱贫进程明显加快，作风治理和能力建设初见成效，精准扶贫、精准脱贫取得突破性进展．为助力我市脱贫攻坚，某村村委会在网上直播销售该村优质农产品礼包，该村在今年1月份销售256包，2、3月该礼包十分畅销，销售量持续走高，在售价不变的基础上，3月份的销售量达到400包．
（1）若设2、3这两个月销售量的月平均增长率为a%，求a的值；
由题意得256(1+a%)2=400，
解得a1=25，a2=−225(舍去)，
即2、3这两个月的月平均增长率为25%，
（2）若农产品礼包成本为每包25元，原售价为每包40元，该村在今年4月进行降价促销，经调查发现，若该农产品礼包每包降价1元，销售量可增加5袋，当农产品礼包每包降价多少元时，这种农产品在4月份可获利4620元？
答：当农产品每袋降价4元时，该农产品在4月份可获利4620元．
解：设当农产品每袋降价m元时，该农产品在4月份可获利4620元．
根据题意可得(40−25−m) (400+5m)=4620，
解得m1=4，m2=−69(舍去)，
例10.有一张长6尺，宽3尺的长方形桌子，现用一块长方形台布铺在桌面上，如果台布的面积是桌面面积的2倍，且四周垂下的长度相同，试求这块台布的长和宽各是多少？（精确到0.1尺）
解：设四周垂下的宽度为x尺时，则台布的长为（2x+6）尺，宽为（2x+3）尺，依题意得：（6+2x）（3+2x）=2×6×3. 整理方程得：2x²+9x-9=0. 解得：x1≈0.84，x2≈-5.3（不合题意，舍去）. 因此：台布的长为：2×0.84+6≈7.7（尺）. 台布的宽为：2×0.84+3≈4.7（尺）. 即这块台布的长约为7.7尺，宽约为4.7尺.
例11.如右图是长方形鸡场的平面示意图.一边靠墙，另三边用竹篱笆围成，且竹篱笆总长为35m.（1）若所围的面积为150m²，试求此长方形鸡场的长和宽；
（2）如果墙长为18m，则（1）中长方形鸡场的长和宽分别是多少？
解：当墙长为18m时，显然BC=20m时，所围成的鸡场会在靠墙处留下一个缺口，不合题意，应舍去，此时所围成的长方形鸡场的长与宽值能是15m和10m.
（3）能围成面积为160m²的长方形鸡场吗？说说你的理由.
解：设道路的宽为x米，依题意得
例12.如图，在一块宽为20m, 长为32m的矩形地面上修筑同样宽的两条道路,余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽为多少？
20×32-32x-20x+x2=540.
解：设道路的宽为 x 米.
(32-x)(20-x)=540.
整理，得x2-52x+100=0.解方程，得（x-50)(x-2）=0.
即 x1=2,x2=50.
当x=50时，32-x=-18,不合题意，舍去.
解：设AB长是x m，依题意得： (100-4x)x=400. 整理得 x2-25x+100=0. 解方程得（x-20）（x-5）=0. 即 x1=5，x2=20. x=20,100-4x=20<25 , x=5,100-4x=80>25 x=5(舍去). 答：羊圈的边长AB和BC的长各是20m,20m.
如图：要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB和BC的长各是多少米？