

人教版九年级上册21.1 一元二次方程精品同步练习题
展开![]() 21.3.1 实际问题与一元二次方程(1)
21.3.1 实际问题与一元二次方程(1)
一、选择题
- 某品牌手机三月份销售 400 万部,四月份、五月份销售量连续增长,五月份销售量达到 900 万部,求月平均增长率.设月平均增长率为 x,根据题意列方程为
A. 4001+x2=900 B. 4001+2x=900
C. 9001−x2=400 D. 4001+x2=900
- 学校要组织一次篮球赛,赛制为单循环,共 21 场比赛,若比赛组织者计划邀请 x 个队参赛,则 x 满足的关系式为
A. 12xx+1=21 B. 12xx−1=21
C. xx+1=21 D. xx−1=21
- 把小圆半径增加 5 cm 得到大圆,面积扩大了 1 倍,则小圆半径为 cm.
A. 5 B. 2.5 C. 52+5 D. 52−5
- 某建筑工程队在工地一边靠墙处,用 81 米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为 440 平方米.为了方便取物,在各个仓库之间留出了 1 米宽的缺口作为通道,在平行于墙的一边留下一个 1 米宽的缺口作小门.若设 AB=x 米,则可列方程
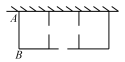
A. x81−4x=440 B. x78−2x=440
C. x84−2x=440 D. x84−4x=440
- 如图是某月的日历表,在此日历表上可以用一个矩形圈出 3×3 个位置相邻的 9 个数(如 6,7,8,13,14,15,20,21,22).若圈出的 9 个数中,最大数与最小数的积为 192,则这 9 个数的和为

A. 32 B. 126 C. 135 D. 144
- 某旅社有 100 张床位,当每床每晚收费 10 元时,客床可全部租出;若每床每晚收费提高 2 元,则减少 10 张床位租出;若每晚收费再提高 2 元,则再减少 10 张床位租出.以每次提高 2 元的方法变化下去,为了投资少且利润大,每床每晚应提高
A. 4 元和 6 元 B. 4 元 C. 6 元 D. 8 元
二、填空题
- 某小区建一长方形草地,其周长为 70 米,对角线长为 25 米,若设长方形草地长为 x 米,则根据题意可列方程为 .
- 如果两数之和为 6,两数之积为 8,那么这两个数为 .
- 如图,某小区有一块长为 36 m,宽为 24 m 的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为 600 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为 m.

- 某超市销售一种水果,每月可售出 500 千克,每千克盈利 10 元.经市场分析,售价每涨 1 元,月销售量将减少 10 千克.如果该超市销售这种水果每月盈利 8000 元,那么该水果的单价涨了多少元?设水果单价涨了 x 元,根据题意,可列方程为 .
- 用一块长 80 cm,宽 60 cm 的纸板,在四个角截去四个相同的小正方形,然后做成一个底面积为 1500 cm2 的无盖长方体纸盒,则截去的小正方形的边长为 .
- 如图,在 Rt△ABC 中,∠BCA=90∘,点 D 是 BC 上一点,AD=BD,若 AB=8,BD=5,则 CD= .

三、解答题
- 如图所示,在 Rt△ABC 中,∠B=90∘,AB=6,BC=12,点 P 从点 B 开始沿边 BA 以 1 cm/s 的速度向点 A 移动,同时点 Q 也从点 B 开始沿 BC 边以 2 cm/s 的速度向点 C 移动.几秒后 △PBQ 的面积是 24 平方厘米?(结果用二次根式表示)

- 某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为 2:1,在温室内,沿前侧内墙保留 3 m 宽的空地,其他三侧内墙各保留 1 m 宽的通道,当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是 288 m2?

- 在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价 80 元,这样按原定票价需花费 6000 元购买的门票张数,现在只花费了 4800 元.
(1) 求每张门票的原定票价;
(2) 根据实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为 324 元,求平均每次降价的百分率.
- 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(CD 边所在的墙长 10 米,DA 边所在的墙足够长),用 28 米长的篱笆围成一个矩形花园 ABCD(篱笆只围 AB,BC 两边),设 AB=x 米.

(1) 若围成花园的面积为 160 平方米,求 x 的值;
(2) 能否围成花园的面积为 300 平方米?说明理由.
- 随着粤港澳大湾区建设的加速推进,广东省正加速布局以 5G 等为代表的战略性新兴产业,据统计,目前广东 5G 基站的数量约 1.5 万座,计划到 2020 年底,全省 5G 基站数是目前的 4 倍,到 2022 年底,全省 5G 基站数量将达到 17.34 万座.
(1) 计划到 2020 年底,全省 5G 基站的数量是多少万座?
(2) 按照计划,求 2020 年底到 2022 年底,全省 5G 基站数量的年平均增长率.
- 某商场按标价销售某种工艺品时,每件可获利 45 元;按标价的八五折销售该工艺品 8 件,与将标价降低 35 元销售该工艺品 12 件所获的利润相等.
(1) 该工艺品每件的进价、标价分别是多少元?
(2) 假设每件工艺品按(1)中求得的进价进货,标价售出,工艺品商场每天可售出该工艺品 100 件.若每件工艺品降价 1 元,则每天可多售出该工艺品 4 件.每件工艺品降价多少元出售,每天获得的利润是 4900 元?
初中数学人教版九年级上册21.3 实际问题与一元二次方程综合训练题: 这是一份初中数学人教版九年级上册21.3 实际问题与一元二次方程综合训练题,共5页。试卷主要包含了5x=182等内容,欢迎下载使用。
初中数学21.3 实际问题与一元二次方程练习题: 这是一份初中数学21.3 实际问题与一元二次方程练习题,共6页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
人教版九年级上册21.3 实际问题与一元二次方程巩固练习: 这是一份人教版九年级上册21.3 实际问题与一元二次方程巩固练习,共5页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。













