






还剩13页未读,
继续阅读
人教版数学八上 14.3.3 因式分解 课件
展开
这是一份人教版数学八上 14.3.3 因式分解 课件,共21页。
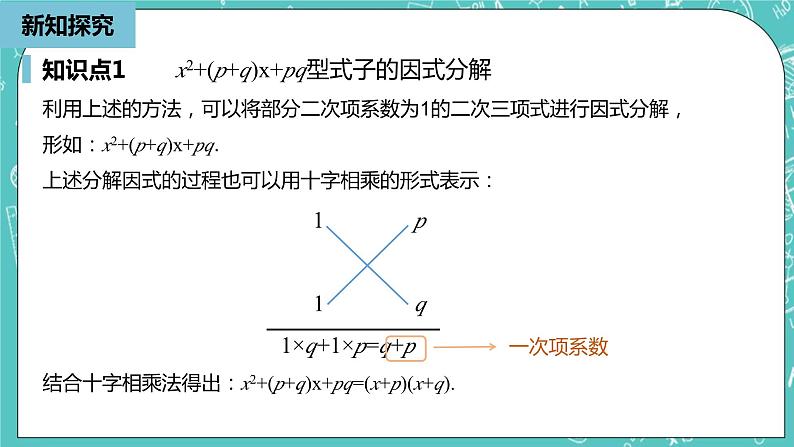
14.3.3 因式分解人教版数学八年级上册知识回顾提公因式法一般步骤:(1) 确定公因式:先确定系数,再确定字母和字母的指数;(2) 提公因式并确定另外一个因式:用多项式除以公因式,所得的商就是提公因式后剩下的另一个因式;(3) 把多项式写成这两个因式的积的形式. 知识回顾因式分解的一般步骤:(1) 当多项式的各项有公因式时,应先提取公因式;当多项式的各项没有公因式时(或提取公因式后),若符合平方差公式或完全平方公式,就利用公式法分解因式;(2) 当不能直接提取公因式或用公式法分解因式时,可根据多项式的特点,把其变形为能提取公因式或能用公式法的形式,再分解因式;(3) 当乘积中的每一个因式都不能再分解时,因式分解就结束了. 一提二套三彻底学习目标1、了解并掌握x2+(p+q)x+pq型式子进行因式分解的方法.2、熟练运用x2+(p+q)x+pq分解因式的方法及步骤进行计算.课堂导入思考:x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子进行因式分解呢?根据已经学过的提公因式法、公式法都不能将x2+(p+q)x+pq进行因式分解.利用多项式的乘法法则推导得出:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq.课堂导入计算下列式子: (x+1)(x+2)=(x-1)(x-2)=(x-1)(x+2)=(x+1)(x-2)=x2+(1+2)x+1×2=x2+3x+2x2-(1+2)x+1×2=x2-3x+2x2+[(-1)+2]x-1×2=x2+x-2x2+[1+(-2)]x-1×2=x2-x-2新知探究知识点1因式分解与整式乘法是方向相反的变形,利用这种关系可以得出: x2+(p+q)x+pq型式子的因式分解二次三项式两个一次二项式的乘积因式分解x2+(p+q)x+pq=(x+p)(x+q)新知探究知识点1利用上述的方法,可以将部分二次项系数为1的二次三项式进行因式分解,形如:x2+(p+q)x+pq.上述分解因式的过程也可以用十字相乘的形式表示: 1 p 1 q 1×q+1×p=q+p 结合十字相乘法得出:x2+(p+q)x+pq=(x+p)(x+q).x2+(p+q)x+pq型式子的因式分解一次项系数新知探究知识点1十字相乘法:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数. 1 4 1 1x2+(p+q)x+pq型式子的因式分解x2+5x+4=(x+1)(x+4)新知探究知识点1 十字相乘法分解因式的步骤:(1) 将二次项系数和常数项竖分为两个因数的乘积(注意:连同符号一起分解);(2) 十字相乘后,若十字相乘的和等于一次项系数,说明因式分解完成;否则继续进行分解,直至十字相乘的和等于一次项系数;(3) 横向写出各分解出的因式.x2+(p+q)x+pq型式子的因式分解新知探究知识点1 重点:(1) 运用x2+(p+q)x+pq=(x+p)(x+q)进行因式分解需要满足的条件:①分解因式的多项式是二次三项式;②二次项系数是1,常数项可以分解成两个数的积,且一次项系数是这两个数的和;(2) 当常数项是正数时,可以分解成两个同号的数的积,符号与一次项的符号相同;当常数项是负数时,可以分解成两个异号的数的积,绝对值大的因数的符号与一次项的符号相同;(3) 有时候需要多次尝试才能分解.x2+(p+q)x+pq型式子的因式分解随堂练习1分解因式:(1) x2-3x+2; (2) x2+3x-10. 解析:(1) 1 -1 常数项2也可以分解为1×2,但此时不能满足一次项 系数,所以不选. 1 -2(2) 1 -2 常数项10也可以分解为2×(-5),1×(-10), 10×(-1),但此时不能满足一次项系数,所以不选. 1 5随堂练习1分解因式:(1) x2-3x+2; (2) x2+3x-10. 解析:(1) 1 -1 1 -2(2) 1 -2 1 5x2-3x+2=(x-1)(x-2)x2+3x-10=(x-2)(x+5)随堂练习2解析:(1) 1 2 常数项10也可以分解为(-2)×(-5),1×(-10), 10×(-1),但此时不能满足一次项系数,所以不选. 1 5(2) 1 2 常数项-8也可以分解为4×(-2),1×(-8), 8×(-1),但此时不能满足一次项系数,所以不选. 1 -4分解因式:(1) x2+7x+10; (2) x2-2x-8. 随堂练习2分解因式:(1) x2+7x+10; (2) x2-2x-8. 解析:(1) 1 2 1 5(2) 1 2 1 -4x2+7x+10=(x+2)(x+5)x2-2x-8=(x+2)(x-4)随堂练习3解析:(1) 1 -2 常数项-2也可以分解为(-1)×2,但此时不能满足一 次项系数,所以不选. 1 1(2) 1 -1 常数项3也可以分解为1×3,但此时不能满足 一次项 系数,所以不选. 1 -3分解因式:(1) m2-m-2; (2) n2-4n+3. 随堂练习3解析:(1) 1 -2 1 1(2) 1 -1 1 -3分解因式:(1) m2-m-2; (2) n2-4n+3. m2-m-2=(m-2)(m+1)n2-4n+3=(n-1)(n-3)课堂小结拓展提升1分解因式:(1) y4+10y2+9; (2) 2m2-8m+6. 解析:(1)将y2看成一个整体a,则原式变形为(y2)2+10y2+9, 可以看作a2+10a+9. (2)观察式子可以先提取公因数2,则原式变形为2(m2-4m+3), 将m2-4m+3因式分解.拓展提升1分解因式:(1) y4+10y2+9; (2) 2m2-8m+6. 拓展提升1分解因式:(1) y4+10y2+9; (2) 2m2-8m+6.
14.3.3 因式分解人教版数学八年级上册知识回顾提公因式法一般步骤:(1) 确定公因式:先确定系数,再确定字母和字母的指数;(2) 提公因式并确定另外一个因式:用多项式除以公因式,所得的商就是提公因式后剩下的另一个因式;(3) 把多项式写成这两个因式的积的形式. 知识回顾因式分解的一般步骤:(1) 当多项式的各项有公因式时,应先提取公因式;当多项式的各项没有公因式时(或提取公因式后),若符合平方差公式或完全平方公式,就利用公式法分解因式;(2) 当不能直接提取公因式或用公式法分解因式时,可根据多项式的特点,把其变形为能提取公因式或能用公式法的形式,再分解因式;(3) 当乘积中的每一个因式都不能再分解时,因式分解就结束了. 一提二套三彻底学习目标1、了解并掌握x2+(p+q)x+pq型式子进行因式分解的方法.2、熟练运用x2+(p+q)x+pq分解因式的方法及步骤进行计算.课堂导入思考:x2+(p+q)x+pq型式子是数学学习中常见的一类多项式,如何将这种类型的式子进行因式分解呢?根据已经学过的提公因式法、公式法都不能将x2+(p+q)x+pq进行因式分解.利用多项式的乘法法则推导得出:(x+p)(x+q)=x2+px+qx+pq=x2+(p+q)x+pq.课堂导入计算下列式子: (x+1)(x+2)=(x-1)(x-2)=(x-1)(x+2)=(x+1)(x-2)=x2+(1+2)x+1×2=x2+3x+2x2-(1+2)x+1×2=x2-3x+2x2+[(-1)+2]x-1×2=x2+x-2x2+[1+(-2)]x-1×2=x2-x-2新知探究知识点1因式分解与整式乘法是方向相反的变形,利用这种关系可以得出: x2+(p+q)x+pq型式子的因式分解二次三项式两个一次二项式的乘积因式分解x2+(p+q)x+pq=(x+p)(x+q)新知探究知识点1利用上述的方法,可以将部分二次项系数为1的二次三项式进行因式分解,形如:x2+(p+q)x+pq.上述分解因式的过程也可以用十字相乘的形式表示: 1 p 1 q 1×q+1×p=q+p 结合十字相乘法得出:x2+(p+q)x+pq=(x+p)(x+q).x2+(p+q)x+pq型式子的因式分解一次项系数新知探究知识点1十字相乘法:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数. 1 4 1 1x2+(p+q)x+pq型式子的因式分解x2+5x+4=(x+1)(x+4)新知探究知识点1 十字相乘法分解因式的步骤:(1) 将二次项系数和常数项竖分为两个因数的乘积(注意:连同符号一起分解);(2) 十字相乘后,若十字相乘的和等于一次项系数,说明因式分解完成;否则继续进行分解,直至十字相乘的和等于一次项系数;(3) 横向写出各分解出的因式.x2+(p+q)x+pq型式子的因式分解新知探究知识点1 重点:(1) 运用x2+(p+q)x+pq=(x+p)(x+q)进行因式分解需要满足的条件:①分解因式的多项式是二次三项式;②二次项系数是1,常数项可以分解成两个数的积,且一次项系数是这两个数的和;(2) 当常数项是正数时,可以分解成两个同号的数的积,符号与一次项的符号相同;当常数项是负数时,可以分解成两个异号的数的积,绝对值大的因数的符号与一次项的符号相同;(3) 有时候需要多次尝试才能分解.x2+(p+q)x+pq型式子的因式分解随堂练习1分解因式:(1) x2-3x+2; (2) x2+3x-10. 解析:(1) 1 -1 常数项2也可以分解为1×2,但此时不能满足一次项 系数,所以不选. 1 -2(2) 1 -2 常数项10也可以分解为2×(-5),1×(-10), 10×(-1),但此时不能满足一次项系数,所以不选. 1 5随堂练习1分解因式:(1) x2-3x+2; (2) x2+3x-10. 解析:(1) 1 -1 1 -2(2) 1 -2 1 5x2-3x+2=(x-1)(x-2)x2+3x-10=(x-2)(x+5)随堂练习2解析:(1) 1 2 常数项10也可以分解为(-2)×(-5),1×(-10), 10×(-1),但此时不能满足一次项系数,所以不选. 1 5(2) 1 2 常数项-8也可以分解为4×(-2),1×(-8), 8×(-1),但此时不能满足一次项系数,所以不选. 1 -4分解因式:(1) x2+7x+10; (2) x2-2x-8. 随堂练习2分解因式:(1) x2+7x+10; (2) x2-2x-8. 解析:(1) 1 2 1 5(2) 1 2 1 -4x2+7x+10=(x+2)(x+5)x2-2x-8=(x+2)(x-4)随堂练习3解析:(1) 1 -2 常数项-2也可以分解为(-1)×2,但此时不能满足一 次项系数,所以不选. 1 1(2) 1 -1 常数项3也可以分解为1×3,但此时不能满足 一次项 系数,所以不选. 1 -3分解因式:(1) m2-m-2; (2) n2-4n+3. 随堂练习3解析:(1) 1 -2 1 1(2) 1 -1 1 -3分解因式:(1) m2-m-2; (2) n2-4n+3. m2-m-2=(m-2)(m+1)n2-4n+3=(n-1)(n-3)课堂小结拓展提升1分解因式:(1) y4+10y2+9; (2) 2m2-8m+6. 解析:(1)将y2看成一个整体a,则原式变形为(y2)2+10y2+9, 可以看作a2+10a+9. (2)观察式子可以先提取公因数2,则原式变形为2(m2-4m+3), 将m2-4m+3因式分解.拓展提升1分解因式:(1) y4+10y2+9; (2) 2m2-8m+6. 拓展提升1分解因式:(1) y4+10y2+9; (2) 2m2-8m+6.
相关资料
更多









