青岛版八年级上册5.6 几何证明举例优质课件ppt

这是一份青岛版八年级上册5.6 几何证明举例优质课件ppt，共15页。PPT课件主要包含了证明得等内容，欢迎下载使用。

1.掌握并证明线段垂直平分线的性质定理与判定定理； 2.掌握基本的证明方法，会通过分析的方法探索证明的思路。
1.什么是线段的垂直平分线？ 2.根据本册第二章的学习你知道线段的垂直平分线有什么性质？ 3.这个性质你是怎样得到的？这个性质是真命题吗？你能用逻辑推理的方法，证明它的真实性吗？
已知：直线 是线段AB的垂直平分线，垂足为点 ，点P是直线 上的任意一点。 求证： =___.
线段垂直平分线上的点到线段两端的距离相等。
“对折”得线段垂直平分线的性质：
分析：要证明边相等，可构造全等三角形，利用全等三角形的性质可得结论：但是当P与M重合时，构不成三角形，需分类讨论.
（1）点P与点M不重合时；（2）点P与点M重合时.
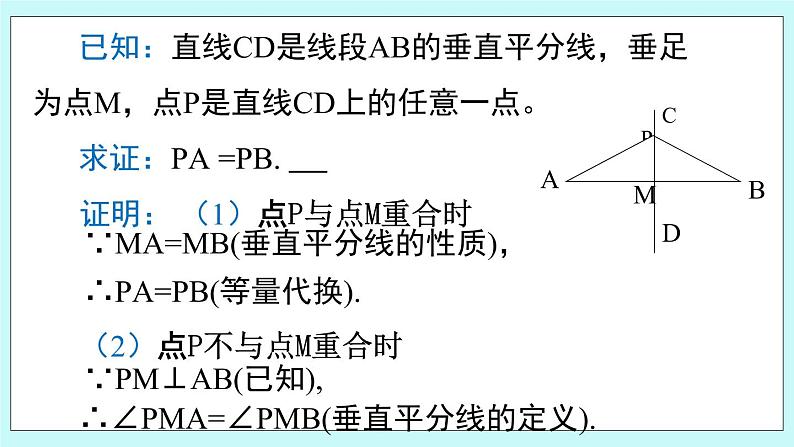
已知：直线CD是线段AB的垂直平分线，垂足为点M，点P是直线CD上的任意一点。 求证：PA =PB.
证明： （1）点P与点M重合时
∵MA=MB(垂直平分线的性质)，
∴PA=PB(等量代换).
（2）点P不与点M重合时
∵PM⊥AB(已知),
∴∠PMA=∠PMB(垂直平分线的定义).
∵PM=PM(公共边)，
MA=MB(垂直平分线的定义).
由(1)(2)可得，该命题成立。
∴△PMA≌△PMB(SAS).
∴PA=PB(全等三角形对应边相等).
线段垂直平分线性质定理的逆命题是什么呢？它是真命题吗？应如何证明它的真实性?
已知：线段AB，P为平面内一点，且PA=PB.求证：点P在线段AB的垂直平分线上.
证明： （1）点P在线段AB所在的直线上，
∵PA=PB(已知)，
∴点P是线段AB的中点(中点的定义)
∴点P在线段AB的垂直平分线上(垂直平分线的定义)
（2）点P不在线段AB所在的直线上，
∴△PAB是等腰三角形.
∴ PC⊥AB (等腰三角形底边上的中线与底边上的高重合).
取AB的中点C，并连接PC.
到一条线段两端的距离相等的点，在这条线段的垂直平分线上。
1.已知：AD⊥BC，BD=DC，点C在AE的垂直平分线上. 求证：AB=AC=CE.
2.已知：如图，AB=AD，BC=DC，E是AC上一点.求证：BE=DE.