资料中包含下列文件，点击文件名可预览资料内容
还剩17页未读，
继续阅读
所属成套资源：8年级人教版数学下册（春季班）同步培优题典
成套系列资料，整套一键下载
初中数学人教版八年级下册19.2.2 一次函数优秀当堂达标检测题
展开
这是一份初中数学人教版八年级下册19.2.2 一次函数优秀当堂达标检测题，文件包含8年级数学下册尖子生同步培优题典专题1910一次函数的应用方案问题教师版docx、8年级数学下册尖子生同步培优题典专题1910一次函数的应用方案问题学生版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
初中数学培优措施和方法
1、拓宽解题思路。数学解题不要局限于本题，而要做到举一反三、多思多想
2、细节决定成败。审题的细节、知识理解的细节、运用公式的细节、忽视检验的细节等，细节决定成败。
3、制作错题集。收集自己的错误，分门别类，没事时就翻一翻，看一看，自警一番，肯定会有很大的收获。
4、查自己欠缺的知识。关键的是做好知识准备，检查漏洞；其次是对解题常犯错误的准备
5、把好的做法形成习惯。注意书写规范，重要步骤不能丢，丢步骤等于丢分。
6、主动思考，全心投入。很多同学在听课的过程中，只是简简单单的听，不能主动思考，这样遇到实际问题时，会无从下手，不知如何应用所学的知识去解答问题。
专题19.10一次函数的应用：方案问题（重难点培优）
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2019春•德阳期末）某电信公司有A、B两种计费方案：月通话费用y（元）与通话时间x（分钟）的关系，如图所示，下列说法中正确的是（ ）
A．月通话时间低于200分钟选B方案划算
B．月通话时间超过300分钟且少于400分钟选A方案划算
C．月通话费用为70元时，A方案比B方案的通话时间长
D．月通话时间在400分钟内，B方案通话费用始终是50元
【分析】根据通话时间少于200分钟时，A、B两方案的费用可判断选项A；根据300＜x＜400时，两函数图象可判断选项B；根据月通话费用为70元时，比较图象的横坐标大小即可判断选项C；根据x≤400，根据图象的纵坐标可判断选项D．
【解析】根据图象可知，当月通话时间低于200分钟时，A方案通话费用始终是30元，B方案通话费用始终是50元，故选项A不合题意；
当300＜x＜400时，A方案通话费用大于70元，B方案通话费用始终是50元，故选项B不合题意；
当月通话费用为70元时，A方案通话费时间为300分钟，B方案通话费时间大于400分钟，故选项C不合题意；
当x≤400时，B方案通话费用始终是50元．故选项D符合题意．
故选：D．
2．（2019•唐县二模）超市有A，B两种型号的瓶子，其容量和价格如表，小张买瓶子用来分装15升油（瓶子都装满，且无剩油）；当日促销活动：购买A型瓶3个或以上，一次性返还现金5元，设购买A型瓶x（个），所需总费用为y（元），则下列说法不一定成立的是（ ）
型号
A
B
单个盒子容量（升）
2
3
单价（元）
5
6
A．购买B型瓶的个数是（5−23x）为正整数时的值
B．购买A型瓶最多为6个
C．y与x之间的函数关系式为y＝x+30
D．小张买瓶子的最少费用是28元
【分析】根据A，B两种型号的瓶子的容量以及买瓶子用来分装15升油（瓶子都装满，且无剩油），可得购买B型瓶的个数是15−2x3，再根据实际意义即可判断A；
根据购买B型瓶的个数是（5−23x）为正整数时的值即可判断B；
分两种情况讨论：①当0≤x＜3时；②当x≥3时，分别求出y与x之间的函数关系式，即可判断C；
根据C中求出的解析式，利用一次函数的性质即可判断D．
【解析】设购买A型瓶x个，
∵买瓶子用来分装15升油，瓶子都装满，且无剩油，
∴购买B型瓶的个数是15−2x3=5−23x，
∵瓶子的个数为自然数，
∴x＝0时，5−23x＝5；x＝3时，5−23x＝3；x＝6时，5−23x＝1；
∴购买B型瓶的个数是（5−23x）为正整数时的值，故A成立；
由上可知，购买A型瓶的个数为0个或3个或6个，所以购买A型瓶的个数最多为6，故B成立；
设购买A型瓶x（个），所需总费用为y（元），则购买B型瓶的个数是（5−23x）个，
①当0≤x＜3时，y＝5x+6×（5−23x）＝x+30，
∵k＝1＞0，
∴y随x的增大而增大，
∴当x＝0时，y有最小值，最小值为30元；
②当x≥3时，y＝5x+6×（5−23x）﹣5＝25+x，
∵k＝1＞0，
∴y随x的增大而增大，
∴当x＝3时，y有最小值，最小值为28元；
综合①②可得，购买盒子所需要最少费用为28元．
故C不成立，D成立．
故选：C．
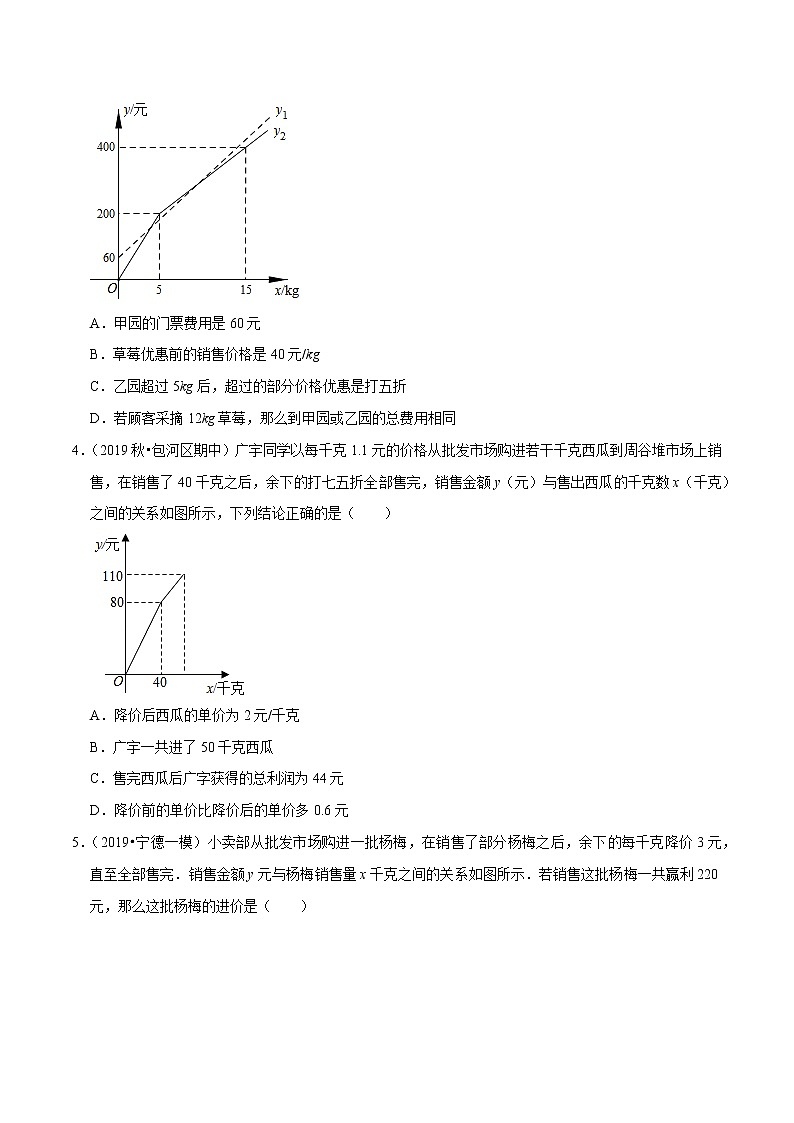
3．（2020•路桥区模拟）甲、乙两个草莓采摘园为吸引顾客，在草莓销售价格相同的基础上分别推出优惠方案，甲园：顾客进园需购买门票，采摘的草莓按六折优惠．乙园：顾客进园免门票，采摘草莓超过一定数量后，超过的部分打折销售．活动期间，某顾客的草莓采摘量为xkg，若在甲园采摘需总费用y1元，若在乙园采摘需总费用y2元．y1，y2与x之间的函数图象如图所示，则下列说法中错误的是（ ）
A．甲园的门票费用是60元
B．草莓优惠前的销售价格是40元/kg
C．乙园超过5kg后，超过的部分价格优惠是打五折
D．若顾客采摘12kg草莓，那么到甲园或乙园的总费用相同
【分析】根据题意和函数图象中的数据，可以判断各个选项中的说法是否正确，从而可以解答本题．
【解析】由图象可得，
甲园的门票为60元，故选项A正确；
乙园草莓优惠前的销售价格是：200÷5＝40（元/千克），故选项B正确；
400−20015−5÷40=0.5，
即乙园超过5kg后，超过的部分价格优惠是打5折，故选项C正确；
若顾客采摘12kg草莓，甲园花费为：60+12×40×0.6＝344（元），乙园的花费为：40×5+（12﹣5）×40×0.5＝340（元），
∵344＞340，
∴若顾客采摘12kg草莓，那么到甲园比到乙园的总费用高，故选项D错误；
故选：D．
4．（2019秋•包河区期中）广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售，在销售了40千克之后，余下的打七五折全部售完，销售金额y（元）与售出西瓜的千克数x（千克）之间的关系如图所示，下列结论正确的是（ ）
A．降价后西瓜的单价为2元/千克
B．广宇一共进了50千克西瓜
C．售完西瓜后广字获得的总利润为44元
D．降价前的单价比降价后的单价多0.6元
【分析】根据题意和函数图象中的数据可以判断出各个选项中的说法是否正确，从而可以解答本题．
【解析】由图可得，
西瓜降价前的价格为：80÷40＝（2元/千克），西瓜降价后的价格为：2×0.75＝1.5（元/千克），故选项A错误，
∵2﹣1.5＝0.5（元），
∴降价前的单价比降价后的单价多0.5元，故选项D错误；
广宇一共进了：40+110−801.5=60千克西瓜，故选项B错误；
售完西瓜后广字获得的总利润为：110﹣1.1×60＝110﹣66＝44（元），故选项C正确；
故选：C．
5．（2019•宁德一模）小卖部从批发市场购进一批杨梅，在销售了部分杨梅之后，余下的每千克降价3元，直至全部售完．销售金额y元与杨梅销售量x千克之间的关系如图所示．若销售这批杨梅一共赢利220元，那么这批杨梅的进价是（ ）
A．10元/千克 B．12元/千克
C．12.5元/千克 D．14.4元/千克
【分析】只需计算出余下的每千克降价3元后的价格即可求
【解析】
由图象知．40千克前的售价为：600÷40＝15元/千克
40千克后，余下的每千克降价3元，可得此时售价为15﹣3＝12元/千克，余下的杨梅：（720﹣600）÷12＝10千克
设进价为t元/千克
则40（15﹣t）+10（12﹣t）＝220
解得t＝10
故选：A．
6．（2019秋•连州市期末）如图是本地区一种产品30天的销售图象，图①是产品日销售量y（单位：件）与时间t（单位：天）的函数关系，图②是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润＝日销售量×一件产品的销售利润，下列结论错误的是（ ）
A．第20天的日销售利润是750元
B．第30天的日销售量为150件
C．第24天的日销售量为200件
D．第30天的日销售利润是750元
【分析】根据题意和函数图象中的数据，可以判断各个选项中的说法是否正确，从而可以解答本题．
【解析】当0≤t≤24时，设y＝kt+b，
b=10024k+b=200，
解得，k=256b=100，
即当0≤t≤24时，y=256t+100，
当t＝20时，y=5006+100≈183，
则第20天的日销售利润约为183×5＝915（元），故选项A错误；
第30天的日销售量为150件，故选项B正确；
第24天的日销售量为200件，故选项C正确；
第30天的日销售利润是150×5＝750（元），故选项D正确；
故选：A．
7．（2020秋•金水区校级期中）甲、乙两个草莓采摘园为吸引顾客，在草莓销售价格相同的基础上分别推出优惠方案，甲园：顾客进园需购买门票，采摘的草莓按六折优惠．乙园：顾客进园免门票，采摘草莓超过一定数量后，超过的部分打折销售．活动期间，某顾客的草莓采摘量为x千克，若在甲园采摘需总费用y1元，若在乙园采摘需总费用y2元．y1，y2与x之间的函数图象如图所示，则下列说法中错误的是（ ）
A．甲园的门票费用是60元
B．草莓优惠前的销售价格是40元/千克
C．乙园超过5千克后，超过的部分价格优惠是打五折
D．若顾客采摘15千克草莓，那么到甲园比到乙园采摘更实惠
【分析】根据题意和函数图象中的数据，可以判断各个选项中的说法是否正确，从而可以解答本题．
【解析】由图象可得，
甲园的门票费用是60元，故选项A正确；
草莓优惠前的销售价格是200÷5＝40（元/千克），故选项B正确；
乙园超过5千克后，超过的部分价格优惠是打400−20015−5÷40×10=5折，故选项C正确；
若顾客采摘15千克草莓，那么到乙园比到甲园采摘更实惠，故选项D错误；
故选：D．
8．（2019•常州模拟）我市某储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开始调出物资（调进物资与调出物资的速度均保持不变）．储运部库存物资S（吨）与时间t（小时）之间的函数关系如图所示，这批物资从开始调进到全部调出需要的时间是（ ）
A．4小时 B．4.3小时 C．4.4小时 D．5小时
【分析】由图中可以看出，2小时调进物资3吨，调进物资共用4小时，说明物资一共有6吨；2小时后，调进物资和调出物资同时进行，4小时时，物资调进完毕，仓库还剩1吨，说明调出速度为：（6﹣1）÷2＝2.5吨/时，需要时间为：6÷2.5时，由此即可求出答案．
【解析】物资一共有6吨，调出速度为：（6﹣1）÷2＝2.5吨/小时，需要时间为：6÷2.5＝2.4（时）
∴这批物资从开始调进到全部调出需要的时间是：2+2.4＝4.4小时．
故选：C．
9．（2019秋•义乌市期末）某公司为调动职工工作积极性，向工会代言人提供了两个加薪方案，要求他从中选择：
方案一：是12个月后，在年薪20000元的基础上每年提高500元（第一年年薪20000元）；
方案二：是6个月后，在半年薪10000元的基础上每半年提高250元（第6个月末发薪水10000元）
但不管是选哪一种方案，公司都是每半年发一次工资，如果你是工会代言人，认为哪种方案对员工更有利？（ ）
A．方案一
B．方案二
C．两种方案一样
D．工龄短的选方案一，工龄长的选方案二
【分析】根据方案一和方案二计算两年工人的年薪便可得出结论．
【解析】∵方案一：是12个月后，在年薪20000元的基础上每年提高500元（第一年年薪20000元），
∴按这种方案计算，第一年年薪为20000元，第二年年薪为20000+500＝20500元，
∵方案二：是6个月后，在半年薪10000元的基础上每半年提高250元（第6个月末发薪水10000元），
∴按这种方案计算，第一年年薪为10000+（10000+250）＝20250元，第二年年薪为（10000+500）+（10000+750）＝21250元，
由上可知，方案二比方案一对员工更有利．
故选：B．
10．（2018秋•武邑县校级期末）为了鼓励居民节约用水，某市决定实行两级收费制度，水费y（元）与用水量x（吨）之间的函数关系如图所示．若每月用水量不超过20吨（含20吨），按政府优惠价收费；若每月用水量超过20吨，超过部分按市场价4元/吨收费，那么政府优惠价是（ ）
A．2.2元/吨 B．2.4元/吨 C．2.6元/吨 D．2.8元/吨
【分析】根据题意和函数图象中的数据，可以求得政府优惠价，本题得以解决．
【解析】设政府优惠价是x元/吨，
20x+（30﹣20）×4＝92，
解得，x＝2.6，
故选：C．
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．（2020春•金平区期末）我国很多城市水资源缺乏，为了加强居民的节水意识，某自来水公司采取分段收费标准，某市居民月交水费y（元）与用水量x（吨）之间的关系如图所示，若某户居民4月份用水20吨，则应交水费 44 元．
【分析】根据函数图象中的数据，可以求得超出10吨水时，每吨水的价格，从而可以计算出某户居民4月份用水20吨，则应交水费多少元．
【解析】由图象可知，
超出10吨的部分，每吨水的价格是（31﹣18）÷（15﹣10）＝2.6（元），
当用水20吨时，应交水费：18+（20﹣10）×2.6＝44（元），
故答案为：44．
12．（2019秋•渝中区校级月考）国庆期间，鲁能巴蜀中学团委决定组织同学们观看电影《我和我的祖国》，《中国机长》和《攀登者》，小明准备到电影院提前购票．已知三部电影单价之和为100元，计划购买三部电影票总共不超过135张；其中《攀登者》票价为30元，计划购买35张，《中国机长》至少购买25张，《我和我的祖国》数量不少于《中国机长》的2倍粗心的小明在做预算时将《我和我的祖国》和《中国机长》的票价弄反了，结果实际购买三种电影票时的总价比预算多了112元，若三部电影票的单价均为整数，则小明实际购买这三部电影票最多需要花费 4046 元．
【分析】设《我和我的祖国》和《中国机长》的电影票单价分别为x元和y元，购《我和我的祖国》和《中国机长》的电影票为a张和b张；根据题意得方程即可解决问题；
【解析】设《我和我的祖国》和《中国机长》的电影票单价分别为x元和y元，购《我和我的祖国》和《中国机长》的电影票为a张和b张；
由题意：x+y＝70，
∴y＝70﹣x，
根据题意得a+b≤100b≥25a≥2b，
解得：25≤a﹣b≤50，
ax+by﹣ax﹣by＝ax+b（70﹣x）﹣a（70﹣x）﹣bx＝ax+70b﹣bx﹣70a+ax﹣bx＝70b﹣70a﹣2bx+2ax＝112
∴ax﹣bx＝35a﹣35b+56，
∴（x﹣35）（a﹣b）＝56＝2×28，
∴x−35=2a−b=28，
解得：x=37a=b+28，
∴b+28≥2b，
∴b≤28，a≤56，
∴b最大＝28，a最大＝56，
∴这三部电影票最多需要花费
ax+by＝ax+b（70﹣x）+35×30＝ax+70b﹣bx+1050＝ax﹣bx+70b+1050＝35a﹣35b+70b+1050＝35a+35b+1050＝，
ax+by＝ax+b（70﹣x）+35×30＝ax+70b﹣bx+1050＝ax﹣bx+70b+1050＝35a﹣35b+70b+1050＝35a﹣35b+56+70b+1050＝35（a+b）+1106≤35×84+1106＝4046，
答：小明实际购买这三部电影票最多需要花费4046元．
故答案为：4046．
13．（2016春•历下区校级期末）如图所示，是某电信公司甲、乙两种业务：每月通话费用y（元）与通话时间x（分）之间的函数关系．某企业的周经理想从两种业务中选择一种，如果周经理每个月的通话时间都在100分钟以上，那么选择 甲 种业务合算．
【分析】根据函数图象可以分别求得甲、乙两种业务对应的函数解析式，从而可以求得两种花费相同情况时的时刻，然后再根据函数图象即可解答本题．
【解析】设乙种业务对应的函数解析式为y＝kx，
则50k＝10，得k＝0.2，
即乙种业务对应的函数解析式为y＝0.2x，
设甲种业务对应的函数解析式为：y＝ax+b，
b=1050a+b=15，解得，a=0.1b=10，
即甲种业务对应的函数解析式为y＝0.1x+10，
∴令0.2x＝0.1x+10，得x＝100，
即当通话时间为100分钟时两种业务花费一样多，
由图象可知，当通话时间在100分钟以上，甲种业务比较合算，
故答案为：甲．
14．（2020•宝应县二模）如图，购买一种苹果，所付款金额y（元）与购买量x（千克）之间的函数图象由线段OA和射线AB组成，如果班级搞一次茶话会，一次购买26千克这种苹果需 4283 元．
【分析】根据函数图象中的数据，可以得到超过3千克后，每千克苹果的价格，然后即可计算出一次购买26千克这种苹果需要的钱数．
【解析】由图象可得，
当x＞3时，每千克苹果的价格是：（36﹣20）÷（6﹣3）=163（元），
∵26＞3，
∴一次购买26千克这种苹果需：20+163×（26﹣3）=4283（元），
故答案为：4283．
15．（2020•浙江自主招生）某市政府大力扶持大学生创业．小甬在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数：y＝﹣10x+500．根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果小甬想要每月获得的利润不低于2000元，那么他每月的成本最少需要 3600 元．（成本＝进价×销售量）
【分析】设成本为P（元），根据题意得出P与x的函数关系式，再根据一次函数的性质解答即可．
【解析】设成本为P（元），由题意，得：P＝20（﹣10x+500）＝﹣200x+10000，
∵a＝﹣200＜0，
∴P随x的增大而减小，
由∵x≤32，
∴当x＝32时，P最小＝3600，
当x＝32时，y＝﹣10×32+500＝180，
（32﹣20）×180＝2160（元），
答：想要每月获得的利润不低于2000元，每月的成本最少为3600元．
故答案为：3600．
16．（2020•历下区校级模拟）某快递公司每天上午9：30﹣10：30为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，那么从9：30开始，经过 20 分钟时，两仓库快递件数相同．
【分析】分别求出甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数关系式，求出两条直线的交点坐标即可．
【解析】设甲仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y1＝k1x+40，根据题意得60k1+40＝400，解得k1＝6，
∴y1＝6x+40；
设乙仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y2＝k2x+240，根据题意得60k2+240＝0，解得k2＝﹣4，
∴y2＝﹣4x+240，
联立y=6x+40y=−4x+240，
解得x=20y=160，
∴经过20分钟时，当两仓库快递件数相同．
故答案为：20
17．（2019秋•广饶县期末）如图，l1表示某机床公司一天的销售收入与机床销售量的关系，l2表示该公司一天的销售成本与机床销售量的关系．有以下四个结论：
①l1对应的函数表达式是y＝x；②l2对应的函数表达式是y＝x+1；
③当销售量为2件时，销售收入等于销售成本；
④利润与销售量之间的函数表达式是w＝0.5x﹣1．
其中正确的结论为 ①③④ （请把所有正确的序号填写在横线上）．
【分析】首先用待定系数法求出解析式，然后根据“利润＝收入﹣成本”可得利润与销售量之间的函数关系式．
【解析】①观察图象可知直线l1经过原点，
设l1的解析式为y1＝kx，
将点（2，2）代入解析式可得 2＝2k，
解得k＝1，
所以l1的解析式为y1＝x，
故①正确；
②观察图象可知直线l2不经过原点，
设l2的解析式为y2＝kx+b，
将点（0，1）、（2，2）代入解析式可得
1=b2=2k+b，
解得k=12b=1，
所以l2的解析式为y2=12x+1，
故②错误；
③观察图象可知，直线l1与直线l2交于点（2，2），
所以，当销售量为2时，销售收入等于销售成本，
故③正确；
④利润w＝y1﹣y2=x−(12x+1)=12x−1，
故④正确；
故答案为①③④
18．（2020春•武川县期末）如图2是本地区一种产品30天的销售图象，图1是产品日销售量y（单位：件）与时间t单位：天）的函数关系，图2是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润＝日销售量×一件产品的销售利润，下列正确结论的序号是 ①②④ ．
①第24天的销售量为200件；
②第10天销售一件产品的利润是15元；
③第12天与第30天这两天的日销售利润相等；
④第30天的日销售利润是750元．
【分析】图1是产品日销售量y（单位：件）与时间t单位：天）的函数图象，观察图象可对①做出判断；通过图2求出z与t的函数关系式，求出当t＝10时z的值，做出判断，分别求出第12天和第30天的销售利润，对③④进行判断，最后综合各个选项得出答案．
【解析】图1反应的是日销售量y与时间t之间的关系图象，过（24，200），因此①是正确的，
由图2可得：z=−t+25(0≤t≤20)5(20＜t≤30)，当t＝10时，z＝15，因此②也是正确的，
第12天的销售利润为：[100+（200﹣100）÷24×12]（25﹣12）＝1950元，第30天的销售利润为：150×5＝750元，
因此③不正确，④正确，
故答案为：①②④．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．（2020春•惠安县期末）某中学为了加强学生体育锻炼，准备购进一批篮球和足球．据调查，某体育器材专卖店销售40个足球和60个篮球一共9200元；销售100个足球和30个篮球一共11000元．
（1）求足球和篮球的单价；
（2）该校计划使用10420元资金用于购买足球和篮球120个，且篮球数量不少于足球数量的2倍．购买时恰逢该专卖店在做优惠活动，信息如表：
球类
购买数量低于50个
购买数量不低于50个
足球
原价销售
八折销售
篮球
原价销售
九折销售
问在使用资金不超额的情况下，可有几种购买方案？如何购买费用最少？
【分析】（1）利用二元一次方程组即可求出足球、篮球的单价，
（2）设购买足球x个，则购买篮球（120﹣x）个，根据题意求出x的取值范围，再根据（1）的结论列不等式即可得出购买方案．
【解析】（1）设足球每个x元，篮球每个y元，由题意得：
40x+60y=9200100x+30y=11000，
解得x=80y=100，
答：足球每个80元，篮球每个100元．
（2）设购买足球x个，则购买篮球（120﹣x）个，根据题意得：
120﹣x≥2x，
解得x≤40，
由题意得：80x+100×0.9（120﹣x）≤10420，
解得x≥38，
∴38≤x≤40，
∵x为正整数，
∴有3种购买方案：①购买足球38个，篮球82个；②购买足球39个，篮球81个；③购买足球40个，篮球80个．
∵购买篮球的单价大于购买足球的单价，所以方案③购买费用最少．
20．（2020春•文水县期末）为了加强环境保护，进一步提升污水处理能力，我县某污水处理厂决定购买A、B两种型号的污水处理设备共20台，每台A型污水处理设备12万元，每台B型污水处理设备10万元，已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨，2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨．
（1）求A、B两种型号污水处理设备每周分别可以处理污水多少吨？
（2）现要求购买A种型号污水处理设备的台数不少于B种型号污水处理设备台数的2倍，问如何设计购买方案，使购买这两种型号污水处理设备的费用最少，最少费用是多少？
【分析】（1）根据1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨，2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨，可以列出相应的二元一次方程组，从而解答本题；
（2）设购买B种型号污水处理设备m台，所需费用为w元，根据题意列不等式求出m的取值范围，再根据题意求出w与m的函数关系式，再根据一次函数的性质解答即可．
【解析】（1）设A种型号污水处理设备每周可以处理污水x吨，B种型号污水处理设备每周可以处理污水y吨，
根据题意得：x+2y=6402x+3y=1080，
解得：x=240y=200，
答：A种型号污水处理设备每周可以处理污水240吨，B种型号污水处理设备每周可以处理污水200吨；
（2）设购买B种型号污水处理设备m台，所需费用为w元，
根据题意得：20﹣m≥2m，
解得：m≤203，
w＝12（20﹣m）+10m＝﹣2m+240，
∵k＝﹣2＜0，
∴w随m的增大而减小，
又∵m≤203且m为正整数，
∴当m＝6时，w有最小值，最小值为：﹣2×6+240＝228（万元），
此时，20﹣m＝14，
答：购买A种型号污水处理设备14台，购买B种型号污水处理设备6台时费用最少，最少费用为228万元．
21．（2020春•大余县期末）为拓宽学生视野，引导学生主动适应社会，我县某中学决定组织部分班级去丫山开展研学旅行活动．在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生，现有甲、乙两种大客车，它们的载客量和租金如下表所示，为了安全既要保证所有师生都有车坐，又要保证每辆车上至少要有2名老师．
甲种客车
乙种客车
载客量（人/辆）
30
42
租金（元/辆）
300
400
（1）参加此次研学旅行活动的老师和学生各有多少人？
（2）设租用两种车共8辆，其中a辆甲种客车，租车总费用为W元．请求出W与a之间的函数关系式（不要求写出a的取值范围）．
（3）在（2）的条件下，学校计划此次研学旅行活动的租车总费用不超过3100元，且保证师生都有座位，请问有哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由．
【分析】（1）设出老师有x名，学生有y名，得出二元一次方程组，解出即可；再由每辆客车上至少要有2名老师，且要保证300名师生有车坐，可得租用客车总数；
（2）由租用a辆甲种客车，得乙种客车数为：（8﹣x）辆，由题意得出W＝300a+400（8﹣a）即可；
（3）由题意得出3200−100a≤310030a+42(8−a)≥300，得出a取值范围，分析得出即可．
【解析】（1）设老师有x名，学生有y名．
依题意，得17x=y−1218x=y+4，解得x=16y=284，
答：此次参加研学旅行活动的老师有16人，学生有284人；
（2）由题意，得：W＝300a+400（8﹣a）＝3200﹣100a；
（3）由题意可得
3200−100a≤310030a+42(8−a)≥300，
解得1≤a≤3（a为整数），
∴共有3 种租车方案：
方案一：租用甲种客车3 辆，乙种客车5 辆，租车费用2900元；
方案二：租用甲种客车2 辆，乙种客车6 辆，租车费用3000元；
方案三：租用甲种客车1辆，乙种客车7 辆，租车费用3100元；
∴最节省费用的租车方案是：租用甲种客车3辆，乙种客车5辆．
22．（2020秋•兴化市期末）供销商场购进甲、乙两种洗衣机共80台进行销售，其中乙洗衣机的数量不超过甲洗衣机的3倍，甲洗衣机每台利润为500元，乙洗衣机每台利润为600元．设购进甲洗衣机x（台），这80台洗衣机全部售出的总利润为W（元）．
（1）求W关于x的函数表达式；
（2）当甲洗衣机购进多少台时，销售总利润最大？最大利润是多少？
【分析】（ 1）根据两种型号的利润的和就是总利润即可列出函数解析式；
（2）根据一次函数的性质，即可求解．
【解析】（1）根据题意得，W＝﹣100x+48000；
（2）∵乙洗衣机的数量不超过甲洗衣机的3倍，
∴80﹣x≤3x，
∴20≤x≤80，
当x＝20时，W的值最大，最大值＝﹣100×20+48000＝46000（元）
答：当甲洗衣机购进20台时，销售总利润最大，最大利润是46000元．
23．（2020秋•余杭区期末）文具店出售书包和文具盒，书包每个定价为30元，文具盒每个定价5元．该店制定了两种优惠方案：
①买一个书包赠送一个文具盒；②按总价的九折付款．
某班学生需购买8个书包和若干个文具盒（不少于8个），设购买文具盒个数为x（个），付款总金额为y（元）．
（1）分别写出两种优惠方案中y与x之间的函数关系式；
（2）请你通过计算，结合购买文具盒的个数说明哪种方案更省钱？
【分析】（1）根据题意，可以分别写出两种优惠方案中y与x之间的函数关系式；
（2）根据题意，可以得到相应的不等式，从而可以解答本题．
【解析】（1）由题意可得，
方案①：y＝30×8+5（x﹣8）＝5x+200（x≥8），
方案②：y＝（30×8+5x）×90%＝4.5x+216（x≥8），
即方案①中中y与x之间的函数关系式是y＝5x+200（x≥8），方案②中y与x的函数关系式为y＝4.5x+216（x≥8）；
（2）当5x+200＝4.5x+216时，解得x＝32；
当5x+200＞4.5x+216时，解得x＞32；
当5x+200＜4.5x+216时，解得x＜32；
即购买文具盒为32个时，两种方案付款相同；购买文具盒超过32个时，方案②更省钱；购买文具盒为少于32个而不少于8个时，方案①更省钱．
24．（2020秋•蜀山区期末）某童装店近两周A、B两款童装的销售情况如下表所示：（进价、售价均保持不变，利润＝售价﹣进价）
销售时段
销售数量（件）
销售收入
A款
B款
第一周
4
5
2050元
第二周
4
9
2890元
（1）求A、B两款童装的销售单价；
（2）若A、B两款童装每件的进价分别为190元、170元，该童装店准备在下个月进这两款童装共50件（每款童装至少进1件），并且在当月全部销售完，请求出该童装店下个月销售这两款童装的最大利润．
【分析】（1）根据题意和表格中的数据，可以列出相应的二元一次方程组，从而可以求得A、B两款童装的销售单价；
（2）根据题意，可以得到利润和购进A款童装件数的函数关系式，然后根据一次函数的性质，即可求得该童装店下个月销售这两款童装的最大利润．
【解析】（1）设A、B两款童装的销售单价分别为a元/件、b元/件，
由表格可得，4a+5b=20504a+9b=2890，
解得a=250b=210，
答：A、B两款童装的销售单价分别为250元/件、210元/件；
（2）设A款童装进x件，则B款童装进（50﹣x）件，利润为w元，
由题意可得，w＝（250﹣190）x+（210﹣170）×（50﹣x）＝20x+2000，
∴w随x的增大而增大，
∵每款童装至少进1件，
∴1≤x≤49，
∴当x＝49时，w取得最大值，此时w＝20×49+2000＝980+2000＝2980，
即该童装店下个月销售这两款童装的最大利润是2980元．
初中数学培优措施和方法
1、拓宽解题思路。数学解题不要局限于本题，而要做到举一反三、多思多想
2、细节决定成败。审题的细节、知识理解的细节、运用公式的细节、忽视检验的细节等，细节决定成败。
3、制作错题集。收集自己的错误，分门别类，没事时就翻一翻，看一看，自警一番，肯定会有很大的收获。
4、查自己欠缺的知识。关键的是做好知识准备，检查漏洞；其次是对解题常犯错误的准备
5、把好的做法形成习惯。注意书写规范，重要步骤不能丢，丢步骤等于丢分。
6、主动思考，全心投入。很多同学在听课的过程中，只是简简单单的听，不能主动思考，这样遇到实际问题时，会无从下手，不知如何应用所学的知识去解答问题。
专题19.10一次函数的应用：方案问题（重难点培优）
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷满分100分，试题共24题，选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2019春•德阳期末）某电信公司有A、B两种计费方案：月通话费用y（元）与通话时间x（分钟）的关系，如图所示，下列说法中正确的是（ ）
A．月通话时间低于200分钟选B方案划算
B．月通话时间超过300分钟且少于400分钟选A方案划算
C．月通话费用为70元时，A方案比B方案的通话时间长
D．月通话时间在400分钟内，B方案通话费用始终是50元
【分析】根据通话时间少于200分钟时，A、B两方案的费用可判断选项A；根据300＜x＜400时，两函数图象可判断选项B；根据月通话费用为70元时，比较图象的横坐标大小即可判断选项C；根据x≤400，根据图象的纵坐标可判断选项D．
【解析】根据图象可知，当月通话时间低于200分钟时，A方案通话费用始终是30元，B方案通话费用始终是50元，故选项A不合题意；
当300＜x＜400时，A方案通话费用大于70元，B方案通话费用始终是50元，故选项B不合题意；
当月通话费用为70元时，A方案通话费时间为300分钟，B方案通话费时间大于400分钟，故选项C不合题意；
当x≤400时，B方案通话费用始终是50元．故选项D符合题意．
故选：D．
2．（2019•唐县二模）超市有A，B两种型号的瓶子，其容量和价格如表，小张买瓶子用来分装15升油（瓶子都装满，且无剩油）；当日促销活动：购买A型瓶3个或以上，一次性返还现金5元，设购买A型瓶x（个），所需总费用为y（元），则下列说法不一定成立的是（ ）
型号
A
B
单个盒子容量（升）
2
3
单价（元）
5
6
A．购买B型瓶的个数是（5−23x）为正整数时的值
B．购买A型瓶最多为6个
C．y与x之间的函数关系式为y＝x+30
D．小张买瓶子的最少费用是28元
【分析】根据A，B两种型号的瓶子的容量以及买瓶子用来分装15升油（瓶子都装满，且无剩油），可得购买B型瓶的个数是15−2x3，再根据实际意义即可判断A；
根据购买B型瓶的个数是（5−23x）为正整数时的值即可判断B；
分两种情况讨论：①当0≤x＜3时；②当x≥3时，分别求出y与x之间的函数关系式，即可判断C；
根据C中求出的解析式，利用一次函数的性质即可判断D．
【解析】设购买A型瓶x个，
∵买瓶子用来分装15升油，瓶子都装满，且无剩油，
∴购买B型瓶的个数是15−2x3=5−23x，
∵瓶子的个数为自然数，
∴x＝0时，5−23x＝5；x＝3时，5−23x＝3；x＝6时，5−23x＝1；
∴购买B型瓶的个数是（5−23x）为正整数时的值，故A成立；
由上可知，购买A型瓶的个数为0个或3个或6个，所以购买A型瓶的个数最多为6，故B成立；
设购买A型瓶x（个），所需总费用为y（元），则购买B型瓶的个数是（5−23x）个，
①当0≤x＜3时，y＝5x+6×（5−23x）＝x+30，
∵k＝1＞0，
∴y随x的增大而增大，
∴当x＝0时，y有最小值，最小值为30元；
②当x≥3时，y＝5x+6×（5−23x）﹣5＝25+x，
∵k＝1＞0，
∴y随x的增大而增大，
∴当x＝3时，y有最小值，最小值为28元；
综合①②可得，购买盒子所需要最少费用为28元．
故C不成立，D成立．
故选：C．
3．（2020•路桥区模拟）甲、乙两个草莓采摘园为吸引顾客，在草莓销售价格相同的基础上分别推出优惠方案，甲园：顾客进园需购买门票，采摘的草莓按六折优惠．乙园：顾客进园免门票，采摘草莓超过一定数量后，超过的部分打折销售．活动期间，某顾客的草莓采摘量为xkg，若在甲园采摘需总费用y1元，若在乙园采摘需总费用y2元．y1，y2与x之间的函数图象如图所示，则下列说法中错误的是（ ）
A．甲园的门票费用是60元
B．草莓优惠前的销售价格是40元/kg
C．乙园超过5kg后，超过的部分价格优惠是打五折
D．若顾客采摘12kg草莓，那么到甲园或乙园的总费用相同
【分析】根据题意和函数图象中的数据，可以判断各个选项中的说法是否正确，从而可以解答本题．
【解析】由图象可得，
甲园的门票为60元，故选项A正确；
乙园草莓优惠前的销售价格是：200÷5＝40（元/千克），故选项B正确；
400−20015−5÷40=0.5，
即乙园超过5kg后，超过的部分价格优惠是打5折，故选项C正确；
若顾客采摘12kg草莓，甲园花费为：60+12×40×0.6＝344（元），乙园的花费为：40×5+（12﹣5）×40×0.5＝340（元），
∵344＞340，
∴若顾客采摘12kg草莓，那么到甲园比到乙园的总费用高，故选项D错误；
故选：D．
4．（2019秋•包河区期中）广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售，在销售了40千克之后，余下的打七五折全部售完，销售金额y（元）与售出西瓜的千克数x（千克）之间的关系如图所示，下列结论正确的是（ ）
A．降价后西瓜的单价为2元/千克
B．广宇一共进了50千克西瓜
C．售完西瓜后广字获得的总利润为44元
D．降价前的单价比降价后的单价多0.6元
【分析】根据题意和函数图象中的数据可以判断出各个选项中的说法是否正确，从而可以解答本题．
【解析】由图可得，
西瓜降价前的价格为：80÷40＝（2元/千克），西瓜降价后的价格为：2×0.75＝1.5（元/千克），故选项A错误，
∵2﹣1.5＝0.5（元），
∴降价前的单价比降价后的单价多0.5元，故选项D错误；
广宇一共进了：40+110−801.5=60千克西瓜，故选项B错误；
售完西瓜后广字获得的总利润为：110﹣1.1×60＝110﹣66＝44（元），故选项C正确；
故选：C．
5．（2019•宁德一模）小卖部从批发市场购进一批杨梅，在销售了部分杨梅之后，余下的每千克降价3元，直至全部售完．销售金额y元与杨梅销售量x千克之间的关系如图所示．若销售这批杨梅一共赢利220元，那么这批杨梅的进价是（ ）
A．10元/千克 B．12元/千克
C．12.5元/千克 D．14.4元/千克
【分析】只需计算出余下的每千克降价3元后的价格即可求
【解析】
由图象知．40千克前的售价为：600÷40＝15元/千克
40千克后，余下的每千克降价3元，可得此时售价为15﹣3＝12元/千克，余下的杨梅：（720﹣600）÷12＝10千克
设进价为t元/千克
则40（15﹣t）+10（12﹣t）＝220
解得t＝10
故选：A．
6．（2019秋•连州市期末）如图是本地区一种产品30天的销售图象，图①是产品日销售量y（单位：件）与时间t（单位：天）的函数关系，图②是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润＝日销售量×一件产品的销售利润，下列结论错误的是（ ）
A．第20天的日销售利润是750元
B．第30天的日销售量为150件
C．第24天的日销售量为200件
D．第30天的日销售利润是750元
【分析】根据题意和函数图象中的数据，可以判断各个选项中的说法是否正确，从而可以解答本题．
【解析】当0≤t≤24时，设y＝kt+b，
b=10024k+b=200，
解得，k=256b=100，
即当0≤t≤24时，y=256t+100，
当t＝20时，y=5006+100≈183，
则第20天的日销售利润约为183×5＝915（元），故选项A错误；
第30天的日销售量为150件，故选项B正确；
第24天的日销售量为200件，故选项C正确；
第30天的日销售利润是150×5＝750（元），故选项D正确；
故选：A．
7．（2020秋•金水区校级期中）甲、乙两个草莓采摘园为吸引顾客，在草莓销售价格相同的基础上分别推出优惠方案，甲园：顾客进园需购买门票，采摘的草莓按六折优惠．乙园：顾客进园免门票，采摘草莓超过一定数量后，超过的部分打折销售．活动期间，某顾客的草莓采摘量为x千克，若在甲园采摘需总费用y1元，若在乙园采摘需总费用y2元．y1，y2与x之间的函数图象如图所示，则下列说法中错误的是（ ）
A．甲园的门票费用是60元
B．草莓优惠前的销售价格是40元/千克
C．乙园超过5千克后，超过的部分价格优惠是打五折
D．若顾客采摘15千克草莓，那么到甲园比到乙园采摘更实惠
【分析】根据题意和函数图象中的数据，可以判断各个选项中的说法是否正确，从而可以解答本题．
【解析】由图象可得，
甲园的门票费用是60元，故选项A正确；
草莓优惠前的销售价格是200÷5＝40（元/千克），故选项B正确；
乙园超过5千克后，超过的部分价格优惠是打400−20015−5÷40×10=5折，故选项C正确；
若顾客采摘15千克草莓，那么到乙园比到甲园采摘更实惠，故选项D错误；
故选：D．
8．（2019•常州模拟）我市某储运部紧急调拨一批物资，调进物资共用4小时，调进物资2小时后开始调出物资（调进物资与调出物资的速度均保持不变）．储运部库存物资S（吨）与时间t（小时）之间的函数关系如图所示，这批物资从开始调进到全部调出需要的时间是（ ）
A．4小时 B．4.3小时 C．4.4小时 D．5小时
【分析】由图中可以看出，2小时调进物资3吨，调进物资共用4小时，说明物资一共有6吨；2小时后，调进物资和调出物资同时进行，4小时时，物资调进完毕，仓库还剩1吨，说明调出速度为：（6﹣1）÷2＝2.5吨/时，需要时间为：6÷2.5时，由此即可求出答案．
【解析】物资一共有6吨，调出速度为：（6﹣1）÷2＝2.5吨/小时，需要时间为：6÷2.5＝2.4（时）
∴这批物资从开始调进到全部调出需要的时间是：2+2.4＝4.4小时．
故选：C．
9．（2019秋•义乌市期末）某公司为调动职工工作积极性，向工会代言人提供了两个加薪方案，要求他从中选择：
方案一：是12个月后，在年薪20000元的基础上每年提高500元（第一年年薪20000元）；
方案二：是6个月后，在半年薪10000元的基础上每半年提高250元（第6个月末发薪水10000元）
但不管是选哪一种方案，公司都是每半年发一次工资，如果你是工会代言人，认为哪种方案对员工更有利？（ ）
A．方案一
B．方案二
C．两种方案一样
D．工龄短的选方案一，工龄长的选方案二
【分析】根据方案一和方案二计算两年工人的年薪便可得出结论．
【解析】∵方案一：是12个月后，在年薪20000元的基础上每年提高500元（第一年年薪20000元），
∴按这种方案计算，第一年年薪为20000元，第二年年薪为20000+500＝20500元，
∵方案二：是6个月后，在半年薪10000元的基础上每半年提高250元（第6个月末发薪水10000元），
∴按这种方案计算，第一年年薪为10000+（10000+250）＝20250元，第二年年薪为（10000+500）+（10000+750）＝21250元，
由上可知，方案二比方案一对员工更有利．
故选：B．
10．（2018秋•武邑县校级期末）为了鼓励居民节约用水，某市决定实行两级收费制度，水费y（元）与用水量x（吨）之间的函数关系如图所示．若每月用水量不超过20吨（含20吨），按政府优惠价收费；若每月用水量超过20吨，超过部分按市场价4元/吨收费，那么政府优惠价是（ ）
A．2.2元/吨 B．2.4元/吨 C．2.6元/吨 D．2.8元/吨
【分析】根据题意和函数图象中的数据，可以求得政府优惠价，本题得以解决．
【解析】设政府优惠价是x元/吨，
20x+（30﹣20）×4＝92，
解得，x＝2.6，
故选：C．
二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上
11．（2020春•金平区期末）我国很多城市水资源缺乏，为了加强居民的节水意识，某自来水公司采取分段收费标准，某市居民月交水费y（元）与用水量x（吨）之间的关系如图所示，若某户居民4月份用水20吨，则应交水费 44 元．
【分析】根据函数图象中的数据，可以求得超出10吨水时，每吨水的价格，从而可以计算出某户居民4月份用水20吨，则应交水费多少元．
【解析】由图象可知，
超出10吨的部分，每吨水的价格是（31﹣18）÷（15﹣10）＝2.6（元），
当用水20吨时，应交水费：18+（20﹣10）×2.6＝44（元），
故答案为：44．
12．（2019秋•渝中区校级月考）国庆期间，鲁能巴蜀中学团委决定组织同学们观看电影《我和我的祖国》，《中国机长》和《攀登者》，小明准备到电影院提前购票．已知三部电影单价之和为100元，计划购买三部电影票总共不超过135张；其中《攀登者》票价为30元，计划购买35张，《中国机长》至少购买25张，《我和我的祖国》数量不少于《中国机长》的2倍粗心的小明在做预算时将《我和我的祖国》和《中国机长》的票价弄反了，结果实际购买三种电影票时的总价比预算多了112元，若三部电影票的单价均为整数，则小明实际购买这三部电影票最多需要花费 4046 元．
【分析】设《我和我的祖国》和《中国机长》的电影票单价分别为x元和y元，购《我和我的祖国》和《中国机长》的电影票为a张和b张；根据题意得方程即可解决问题；
【解析】设《我和我的祖国》和《中国机长》的电影票单价分别为x元和y元，购《我和我的祖国》和《中国机长》的电影票为a张和b张；
由题意：x+y＝70，
∴y＝70﹣x，
根据题意得a+b≤100b≥25a≥2b，
解得：25≤a﹣b≤50，
ax+by﹣ax﹣by＝ax+b（70﹣x）﹣a（70﹣x）﹣bx＝ax+70b﹣bx﹣70a+ax﹣bx＝70b﹣70a﹣2bx+2ax＝112
∴ax﹣bx＝35a﹣35b+56，
∴（x﹣35）（a﹣b）＝56＝2×28，
∴x−35=2a−b=28，
解得：x=37a=b+28，
∴b+28≥2b，
∴b≤28，a≤56，
∴b最大＝28，a最大＝56，
∴这三部电影票最多需要花费
ax+by＝ax+b（70﹣x）+35×30＝ax+70b﹣bx+1050＝ax﹣bx+70b+1050＝35a﹣35b+70b+1050＝35a+35b+1050＝，
ax+by＝ax+b（70﹣x）+35×30＝ax+70b﹣bx+1050＝ax﹣bx+70b+1050＝35a﹣35b+70b+1050＝35a﹣35b+56+70b+1050＝35（a+b）+1106≤35×84+1106＝4046，
答：小明实际购买这三部电影票最多需要花费4046元．
故答案为：4046．
13．（2016春•历下区校级期末）如图所示，是某电信公司甲、乙两种业务：每月通话费用y（元）与通话时间x（分）之间的函数关系．某企业的周经理想从两种业务中选择一种，如果周经理每个月的通话时间都在100分钟以上，那么选择 甲 种业务合算．
【分析】根据函数图象可以分别求得甲、乙两种业务对应的函数解析式，从而可以求得两种花费相同情况时的时刻，然后再根据函数图象即可解答本题．
【解析】设乙种业务对应的函数解析式为y＝kx，
则50k＝10，得k＝0.2，
即乙种业务对应的函数解析式为y＝0.2x，
设甲种业务对应的函数解析式为：y＝ax+b，
b=1050a+b=15，解得，a=0.1b=10，
即甲种业务对应的函数解析式为y＝0.1x+10，
∴令0.2x＝0.1x+10，得x＝100，
即当通话时间为100分钟时两种业务花费一样多，
由图象可知，当通话时间在100分钟以上，甲种业务比较合算，
故答案为：甲．
14．（2020•宝应县二模）如图，购买一种苹果，所付款金额y（元）与购买量x（千克）之间的函数图象由线段OA和射线AB组成，如果班级搞一次茶话会，一次购买26千克这种苹果需 4283 元．
【分析】根据函数图象中的数据，可以得到超过3千克后，每千克苹果的价格，然后即可计算出一次购买26千克这种苹果需要的钱数．
【解析】由图象可得，
当x＞3时，每千克苹果的价格是：（36﹣20）÷（6﹣3）=163（元），
∵26＞3，
∴一次购买26千克这种苹果需：20+163×（26﹣3）=4283（元），
故答案为：4283．
15．（2020•浙江自主招生）某市政府大力扶持大学生创业．小甬在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似地看作一次函数：y＝﹣10x+500．根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果小甬想要每月获得的利润不低于2000元，那么他每月的成本最少需要 3600 元．（成本＝进价×销售量）
【分析】设成本为P（元），根据题意得出P与x的函数关系式，再根据一次函数的性质解答即可．
【解析】设成本为P（元），由题意，得：P＝20（﹣10x+500）＝﹣200x+10000，
∵a＝﹣200＜0，
∴P随x的增大而减小，
由∵x≤32，
∴当x＝32时，P最小＝3600，
当x＝32时，y＝﹣10×32+500＝180，
（32﹣20）×180＝2160（元），
答：想要每月获得的利润不低于2000元，每月的成本最少为3600元．
故答案为：3600．
16．（2020•历下区校级模拟）某快递公司每天上午9：30﹣10：30为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数图象如图所示，那么从9：30开始，经过 20 分钟时，两仓库快递件数相同．
【分析】分别求出甲、乙两仓库的快件数量y（件）与时间x（分）之间的函数关系式，求出两条直线的交点坐标即可．
【解析】设甲仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y1＝k1x+40，根据题意得60k1+40＝400，解得k1＝6，
∴y1＝6x+40；
设乙仓库的快件数量y（件）与时间x（分）之间的函数关系式为：y2＝k2x+240，根据题意得60k2+240＝0，解得k2＝﹣4，
∴y2＝﹣4x+240，
联立y=6x+40y=−4x+240，
解得x=20y=160，
∴经过20分钟时，当两仓库快递件数相同．
故答案为：20
17．（2019秋•广饶县期末）如图，l1表示某机床公司一天的销售收入与机床销售量的关系，l2表示该公司一天的销售成本与机床销售量的关系．有以下四个结论：
①l1对应的函数表达式是y＝x；②l2对应的函数表达式是y＝x+1；
③当销售量为2件时，销售收入等于销售成本；
④利润与销售量之间的函数表达式是w＝0.5x﹣1．
其中正确的结论为 ①③④ （请把所有正确的序号填写在横线上）．
【分析】首先用待定系数法求出解析式，然后根据“利润＝收入﹣成本”可得利润与销售量之间的函数关系式．
【解析】①观察图象可知直线l1经过原点，
设l1的解析式为y1＝kx，
将点（2，2）代入解析式可得 2＝2k，
解得k＝1，
所以l1的解析式为y1＝x，
故①正确；
②观察图象可知直线l2不经过原点，
设l2的解析式为y2＝kx+b，
将点（0，1）、（2，2）代入解析式可得
1=b2=2k+b，
解得k=12b=1，
所以l2的解析式为y2=12x+1，
故②错误；
③观察图象可知，直线l1与直线l2交于点（2，2），
所以，当销售量为2时，销售收入等于销售成本，
故③正确；
④利润w＝y1﹣y2=x−(12x+1)=12x−1，
故④正确；
故答案为①③④
18．（2020春•武川县期末）如图2是本地区一种产品30天的销售图象，图1是产品日销售量y（单位：件）与时间t单位：天）的函数关系，图2是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润＝日销售量×一件产品的销售利润，下列正确结论的序号是 ①②④ ．
①第24天的销售量为200件；
②第10天销售一件产品的利润是15元；
③第12天与第30天这两天的日销售利润相等；
④第30天的日销售利润是750元．
【分析】图1是产品日销售量y（单位：件）与时间t单位：天）的函数图象，观察图象可对①做出判断；通过图2求出z与t的函数关系式，求出当t＝10时z的值，做出判断，分别求出第12天和第30天的销售利润，对③④进行判断，最后综合各个选项得出答案．
【解析】图1反应的是日销售量y与时间t之间的关系图象，过（24，200），因此①是正确的，
由图2可得：z=−t+25(0≤t≤20)5(20＜t≤30)，当t＝10时，z＝15，因此②也是正确的，
第12天的销售利润为：[100+（200﹣100）÷24×12]（25﹣12）＝1950元，第30天的销售利润为：150×5＝750元，
因此③不正确，④正确，
故答案为：①②④．
三、解答题（本大题共6小题，共46分．解答时应写出文字说明、证明过程或演算步骤）
19．（2020春•惠安县期末）某中学为了加强学生体育锻炼，准备购进一批篮球和足球．据调查，某体育器材专卖店销售40个足球和60个篮球一共9200元；销售100个足球和30个篮球一共11000元．
（1）求足球和篮球的单价；
（2）该校计划使用10420元资金用于购买足球和篮球120个，且篮球数量不少于足球数量的2倍．购买时恰逢该专卖店在做优惠活动，信息如表：
球类
购买数量低于50个
购买数量不低于50个
足球
原价销售
八折销售
篮球
原价销售
九折销售
问在使用资金不超额的情况下，可有几种购买方案？如何购买费用最少？
【分析】（1）利用二元一次方程组即可求出足球、篮球的单价，
（2）设购买足球x个，则购买篮球（120﹣x）个，根据题意求出x的取值范围，再根据（1）的结论列不等式即可得出购买方案．
【解析】（1）设足球每个x元，篮球每个y元，由题意得：
40x+60y=9200100x+30y=11000，
解得x=80y=100，
答：足球每个80元，篮球每个100元．
（2）设购买足球x个，则购买篮球（120﹣x）个，根据题意得：
120﹣x≥2x，
解得x≤40，
由题意得：80x+100×0.9（120﹣x）≤10420，
解得x≥38，
∴38≤x≤40，
∵x为正整数，
∴有3种购买方案：①购买足球38个，篮球82个；②购买足球39个，篮球81个；③购买足球40个，篮球80个．
∵购买篮球的单价大于购买足球的单价，所以方案③购买费用最少．
20．（2020春•文水县期末）为了加强环境保护，进一步提升污水处理能力，我县某污水处理厂决定购买A、B两种型号的污水处理设备共20台，每台A型污水处理设备12万元，每台B型污水处理设备10万元，已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨，2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨．
（1）求A、B两种型号污水处理设备每周分别可以处理污水多少吨？
（2）现要求购买A种型号污水处理设备的台数不少于B种型号污水处理设备台数的2倍，问如何设计购买方案，使购买这两种型号污水处理设备的费用最少，最少费用是多少？
【分析】（1）根据1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨，2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨，可以列出相应的二元一次方程组，从而解答本题；
（2）设购买B种型号污水处理设备m台，所需费用为w元，根据题意列不等式求出m的取值范围，再根据题意求出w与m的函数关系式，再根据一次函数的性质解答即可．
【解析】（1）设A种型号污水处理设备每周可以处理污水x吨，B种型号污水处理设备每周可以处理污水y吨，
根据题意得：x+2y=6402x+3y=1080，
解得：x=240y=200，
答：A种型号污水处理设备每周可以处理污水240吨，B种型号污水处理设备每周可以处理污水200吨；
（2）设购买B种型号污水处理设备m台，所需费用为w元，
根据题意得：20﹣m≥2m，
解得：m≤203，
w＝12（20﹣m）+10m＝﹣2m+240，
∵k＝﹣2＜0，
∴w随m的增大而减小，
又∵m≤203且m为正整数，
∴当m＝6时，w有最小值，最小值为：﹣2×6+240＝228（万元），
此时，20﹣m＝14，
答：购买A种型号污水处理设备14台，购买B种型号污水处理设备6台时费用最少，最少费用为228万元．
21．（2020春•大余县期末）为拓宽学生视野，引导学生主动适应社会，我县某中学决定组织部分班级去丫山开展研学旅行活动．在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生，现有甲、乙两种大客车，它们的载客量和租金如下表所示，为了安全既要保证所有师生都有车坐，又要保证每辆车上至少要有2名老师．
甲种客车
乙种客车
载客量（人/辆）
30
42
租金（元/辆）
300
400
（1）参加此次研学旅行活动的老师和学生各有多少人？
（2）设租用两种车共8辆，其中a辆甲种客车，租车总费用为W元．请求出W与a之间的函数关系式（不要求写出a的取值范围）．
（3）在（2）的条件下，学校计划此次研学旅行活动的租车总费用不超过3100元，且保证师生都有座位，请问有哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由．
【分析】（1）设出老师有x名，学生有y名，得出二元一次方程组，解出即可；再由每辆客车上至少要有2名老师，且要保证300名师生有车坐，可得租用客车总数；
（2）由租用a辆甲种客车，得乙种客车数为：（8﹣x）辆，由题意得出W＝300a+400（8﹣a）即可；
（3）由题意得出3200−100a≤310030a+42(8−a)≥300，得出a取值范围，分析得出即可．
【解析】（1）设老师有x名，学生有y名．
依题意，得17x=y−1218x=y+4，解得x=16y=284，
答：此次参加研学旅行活动的老师有16人，学生有284人；
（2）由题意，得：W＝300a+400（8﹣a）＝3200﹣100a；
（3）由题意可得
3200−100a≤310030a+42(8−a)≥300，
解得1≤a≤3（a为整数），
∴共有3 种租车方案：
方案一：租用甲种客车3 辆，乙种客车5 辆，租车费用2900元；
方案二：租用甲种客车2 辆，乙种客车6 辆，租车费用3000元；
方案三：租用甲种客车1辆，乙种客车7 辆，租车费用3100元；
∴最节省费用的租车方案是：租用甲种客车3辆，乙种客车5辆．
22．（2020秋•兴化市期末）供销商场购进甲、乙两种洗衣机共80台进行销售，其中乙洗衣机的数量不超过甲洗衣机的3倍，甲洗衣机每台利润为500元，乙洗衣机每台利润为600元．设购进甲洗衣机x（台），这80台洗衣机全部售出的总利润为W（元）．
（1）求W关于x的函数表达式；
（2）当甲洗衣机购进多少台时，销售总利润最大？最大利润是多少？
【分析】（ 1）根据两种型号的利润的和就是总利润即可列出函数解析式；
（2）根据一次函数的性质，即可求解．
【解析】（1）根据题意得，W＝﹣100x+48000；
（2）∵乙洗衣机的数量不超过甲洗衣机的3倍，
∴80﹣x≤3x，
∴20≤x≤80，
当x＝20时，W的值最大，最大值＝﹣100×20+48000＝46000（元）
答：当甲洗衣机购进20台时，销售总利润最大，最大利润是46000元．
23．（2020秋•余杭区期末）文具店出售书包和文具盒，书包每个定价为30元，文具盒每个定价5元．该店制定了两种优惠方案：
①买一个书包赠送一个文具盒；②按总价的九折付款．
某班学生需购买8个书包和若干个文具盒（不少于8个），设购买文具盒个数为x（个），付款总金额为y（元）．
（1）分别写出两种优惠方案中y与x之间的函数关系式；
（2）请你通过计算，结合购买文具盒的个数说明哪种方案更省钱？
【分析】（1）根据题意，可以分别写出两种优惠方案中y与x之间的函数关系式；
（2）根据题意，可以得到相应的不等式，从而可以解答本题．
【解析】（1）由题意可得，
方案①：y＝30×8+5（x﹣8）＝5x+200（x≥8），
方案②：y＝（30×8+5x）×90%＝4.5x+216（x≥8），
即方案①中中y与x之间的函数关系式是y＝5x+200（x≥8），方案②中y与x的函数关系式为y＝4.5x+216（x≥8）；
（2）当5x+200＝4.5x+216时，解得x＝32；
当5x+200＞4.5x+216时，解得x＞32；
当5x+200＜4.5x+216时，解得x＜32；
即购买文具盒为32个时，两种方案付款相同；购买文具盒超过32个时，方案②更省钱；购买文具盒为少于32个而不少于8个时，方案①更省钱．
24．（2020秋•蜀山区期末）某童装店近两周A、B两款童装的销售情况如下表所示：（进价、售价均保持不变，利润＝售价﹣进价）
销售时段
销售数量（件）
销售收入
A款
B款
第一周
4
5
2050元
第二周
4
9
2890元
（1）求A、B两款童装的销售单价；
（2）若A、B两款童装每件的进价分别为190元、170元，该童装店准备在下个月进这两款童装共50件（每款童装至少进1件），并且在当月全部销售完，请求出该童装店下个月销售这两款童装的最大利润．
【分析】（1）根据题意和表格中的数据，可以列出相应的二元一次方程组，从而可以求得A、B两款童装的销售单价；
（2）根据题意，可以得到利润和购进A款童装件数的函数关系式，然后根据一次函数的性质，即可求得该童装店下个月销售这两款童装的最大利润．
【解析】（1）设A、B两款童装的销售单价分别为a元/件、b元/件，
由表格可得，4a+5b=20504a+9b=2890，
解得a=250b=210，
答：A、B两款童装的销售单价分别为250元/件、210元/件；
（2）设A款童装进x件，则B款童装进（50﹣x）件，利润为w元，
由题意可得，w＝（250﹣190）x+（210﹣170）×（50﹣x）＝20x+2000，
∴w随x的增大而增大，
∵每款童装至少进1件，
∴1≤x≤49，
∴当x＝49时，w取得最大值，此时w＝20×49+2000＝980+2000＝2980，
即该童装店下个月销售这两款童装的最大利润是2980元．
相关试卷
人教版八年级下册19.2.2 一次函数优秀课后作业题： 这是一份人教版八年级下册19.2.2 一次函数优秀课后作业题，文件包含8年级数学下册尖子生同步培优题典专题199一次函数的应用行程问题教师版docx、8年级数学下册尖子生同步培优题典专题199一次函数的应用行程问题学生版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。
初中人教版第十七章 勾股定理17.1 勾股定理精品当堂检测题： 这是一份初中人教版第十七章 勾股定理17.1 勾股定理精品当堂检测题，文件包含8年级数学下册尖子生同步培优题典专题177勾股定理与翻折问题教师版docx、8年级数学下册尖子生同步培优题典专题177勾股定理与翻折问题学生版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
初中数学人教版八年级下册17.1 勾股定理精品练习题： 这是一份初中数学人教版八年级下册17.1 勾股定理精品练习题，文件包含8年级数学下册尖子生同步培优题典专题175勾股定理与弦图问题教师版docx、8年级数学下册尖子生同步培优题典专题175勾股定理与弦图问题学生版docx等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。
