2020-2021学年第二章 实数1 认识无理数同步测试题

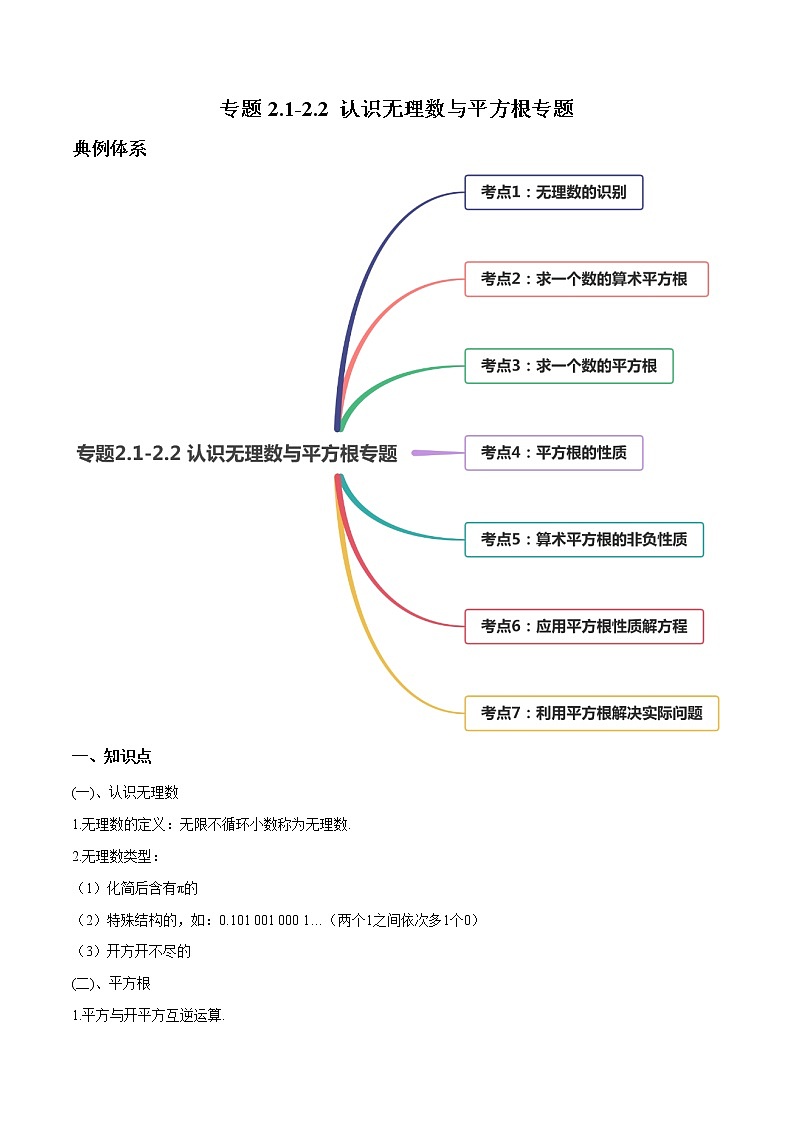
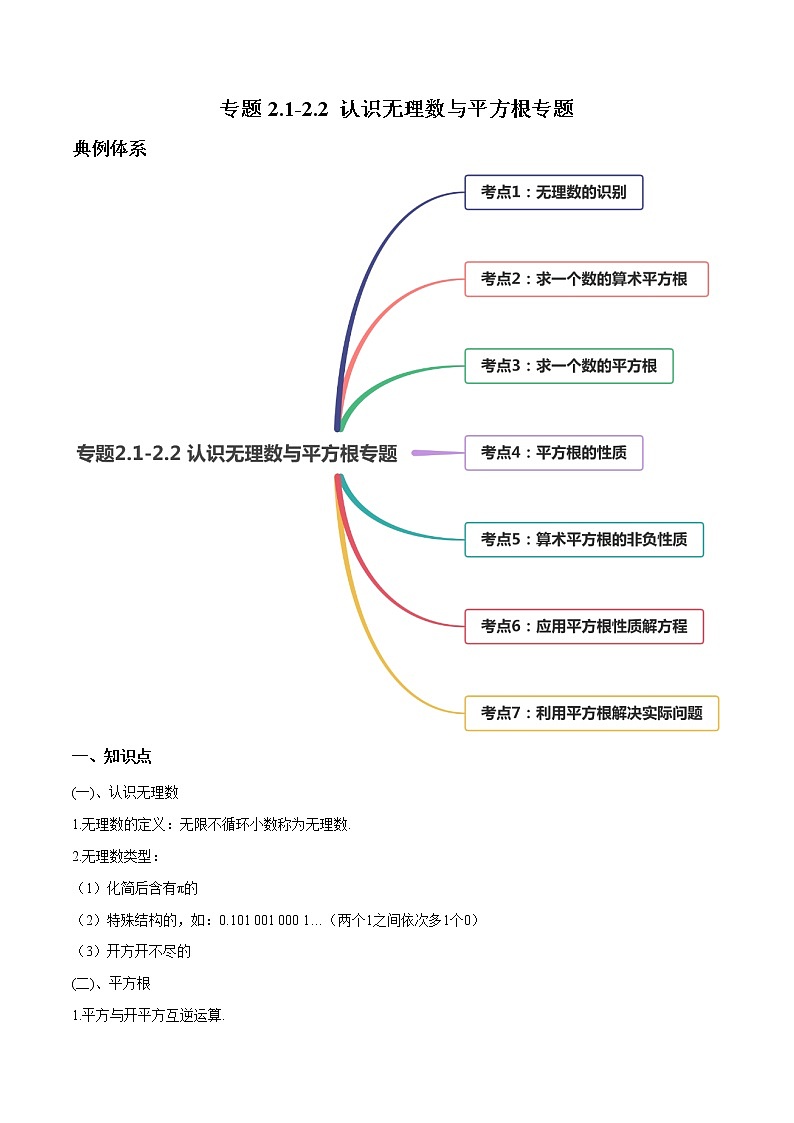
专题2.1-2.2 认识无理数与平方根专题

典例体系

一、知识点

(一)、认识无理数

1.无理数的定义：无限不循环小数称为无理数.

2.无理数类型：

（1）化简后含有π的

（2）特殊结构的，如：0.101 001 000 1…（两个1之间依次多1个0）

（3）开方开不尽的

(二)、平方根

1.平方与开平方互逆运算.

2.补充：一个正数有两个平方根,它们是互为相反数.

0的平方根是0

负数没有平方根

3.平方根与算术平方根的区别和联系.

联系：1.包含关系：平方根包含算术平方根，算术平方根是平方根的一种.

2. 只有非负数才有平方根和算术平方根.

3.0的平方根是0，算术平方根也是0.

区别：1.个数不同：一个正数有两个平方根，但只有一个算术平方根.

2.表示法不同：平方根表示为，而算术平方根表示为.

注:非平方数的算术平方根只能用根号表示.

(三)、算术平方根：

总结：算术平方根具有双重非负性.

①被开方数a是非负数，即：中的a≥0；

②算术平方根本身是非负数，即≥0。

补充：非负性形式有：，，

二、考点点拨与训练

考点1：无理数的识别

典例：（2020·黑龙江嘉荫初一期末）有下列说法：

（1）无理数就是开方开不尽的数；（2）无理数包括正无理数、零、负无理数；

（3）无理数是无限不循环小数；（4）无理数都可以用数轴上的点来表示．

其中正确的说法的个数是(　　)

A．1 B．2 C．3 D．4

【答案】B

【解析】解：（1）无理数就是开方开不尽的数，例如：2.121121112……（每两个2之间多一个1）是无理数，但不是开方开不尽的数，故错误；

（2）零不是无理数，故错误；

（3）无理数是无限不循环小数，故正确；

（4）数轴上的点与实数一一对应，故无理数也可以在数轴上表示，故正确；

综上，正确的说法只有2个．

故答案为B．

方法或规律点拨

本题考查了无理数，掌握无理数是无限不循环小数是解答本题的关键．

巩固练习

1．（2020·厦门市湖滨中学初一期末）下列实数中，是无理数的为（    ）

A． B． C．0 D．2.123122312223

【答案】B

【解析】解：，0，2.123122312223是有理数；是无理数．

故选B．

2．（2020·陕西碑林西北工业大学附属中学初一期末）下列数是无理数的是（　　）

A．π B．﹣ C．|﹣2| D．

【答案】A

【解析】解：A，π是无限不循环小数，属于无理数；

B，是分数，属于有理数；

C，，是整数，属于有理数；

D，是循环小数，属于有理数．

故选：A．

3．（2020·河南省实验中学初三其他）下列实数中：①0.333；②；③；④6.181181118l1118……（每两个8之间的1的个数往后依次增加1个）无理数的个数是（  ）

A．1个 B．2个 C．3个 D．4个

【答案】B

【解析】

根据无理数的定义，是无理数的有：③ ；④6.181181118l1118……（每两个8之间的1的个数往后依次增加1个）共两个，

故选：B．

4．（2019·广东恩平初一期中）在实数：，1，（的个数依次递增），，，中，无理数有（    ）

A．个 B．个 C．个 D．个

【答案】B

【解析】解：不是无理数；

1不是无理数；

（的个数依次递增）是无理数；

不是无理数；

3π是无理数；

=0.33333……，不是无理数；

故在这些数中只有两个无理数，

故选：B．

考点2：求一个数的算术平方根

典例：（2020·北京海淀清华附中初一期末）16的算术平方根是(   ).

A．8 B．－8 C．4 D．±4

【答案】C

【解析】=4，

故选：C.

方法或规律点拨

此题考查算术平方根，解题关键在于掌握运算法则.

巩固练习

1．（2020·广东罗湖深圳中学初三三模）4的算术平方根是（     ）

A．-2 B．2 C． D．

【答案】B

【解析】因，根据算术平方根的定义即可得4的算术平方根是2．故答案选B．

2．（2020·湖北襄城初一期末）81的算术平方根是

A．3 B． C． D．9

【答案】D

【解析】81的算术平方根是,

故选：D．

3．（2020·福建新罗初一期末）25的算术平方根是（    ）

A．5 B． C．12.5 D．

【答案】A

【解析】解：25的算术平方根是5，

故选：5．

4．（2018·河南汝阳初二期末）的值是（　　）

A．7 B．﹣1 C．1 D．﹣7

【答案】A

【解析】=3+4=7，

故选A．

5．（2019·河南伊川初二期末）的算术平方根是（　　）

A．4 B．±4 C．2 D．±2

【答案】C

【解析】＝4，

4的算术平方根是2，

所以的算术平方根是2，

故选C．

6．（2020·黑龙江绥棱初一期末）的算术平方根是________

【答案】

【解析】解：∵，

∴的算术平方根是；

故答案为：．

考点3：求一个数的平方根

典例：（2020·昆明市官渡区第一中学初一期中）的平方根是（    ）

A．9 B．9或－9 C．3 D．3或－3

【答案】D

【解析】解：∵=9

∴的平方根为3或－3

故选D．

方法或规律点拨

此题考查的是算术平方根和平方根的计算，掌握算术平方根的定义和平方根的定义是解决此题的关键．

巩固练习

1．（2020·南丹县八圩瑶族乡初级中学初一期中）16的平方根是（　　）

A．4 B．－4 C．±4 D．±2

【答案】C

【解析】16 的平方根是，

故选C.

2．（2020·安徽濉溪初一期末）的平方根是（    ）

A． B． C． D．没有平方根

【答案】C

【解析】解：，

16的平方根是．

故选：C．

3．（2020·内蒙古呼伦贝尔初三二模）的平方根是（  ）

A． B． C． D．

【答案】C

【解析】解：=64，

64的平方根是±8，

即的平方根是±8.

故选：C.

4．（2020·金昌市金川总校第五中学初一期末）的平方根为（　　）

A．4 B．﹣4 C．±2 D．2

【答案】C

【解析】解：，

所以的平方根为：±2.

故选C.

5．（2020·江西广丰初一期末）平方根等于它自己的数是（   ）

A．0 B．1 C． D．

【答案】A

【解析】解：平方根等于它本身的数是0，

故选A．

考点4：平方根的性质

典例：（2020·南丹县八圩瑶族乡初级中学初一期中）已知x﹣6与3x+14是一个正数的平方根，求这个正数．

【答案】256或64．

【解析】解：当x﹣6=3x+14时，x=-10，

∴这个正数为（x-6）2=（-10-6）2=256；

当x﹣6+3x+14=0时，x=-2

∴这个正数为（x-6）2=（-2-6）2=64

故这个正数是256或64．

方法或规律点拨

本题考查了平方根的概念．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．

巩固练习

1．（2020·山东高唐初二期中）一个正数的两个平方根分别是与，则a的值为(　　 )

A．-1 B．1 C．-2 D．2

【答案】A

【解析】∵一个正数的两个平方根分别是2a−1与−a+2，

∴，解得：.

故选A.

2．（2020·北京首师大附中通州校区初一期末）一个正数的两个不同的平方根是 a +3和2 a－6，则这个正数是(  )

A．1. B．4. C．9. D．16.

【答案】D

【解析】解：由题意得，

a+3+2a-6=0，

∴a=1，

∴a+3=4,

∴这个正数是42=16.

故选D.

3．（2020·昆明市官渡区第一中学初一期中）已知一个正数的两个平方根分别是和，则这个正数为_____．

【答案】121

【解析】解：∵一个正数的两个平方根分别是和，

∴+=0，解得：a=3，

∴这个正数是．

故答案为：121．

4．（2020·山东寿光初二期末）正数的两个平方根分别是和，则这个正数是___________．

【答案】121

【解析】根据题意得：，

解得：，

可得这个正数的两个平方根为11和-11，

则这个正数为121．

故答案为：121．

5．（2020·北京北师大实验中学初一期中）若一个正数的平方根是和，则__________，__________．

【答案】-1    9   

【解析】解：若一个正数的平方根是和，

则和互为相反数，即，

解得：，

则，，

则这个正数x为9，

故答案为-1；9.

6．（2020·内蒙古海勃湾初一期末）若 2a-1和a-1是一个正数?的两个平方根，则?=_____．

【答案】

【解析】解：∵2a－1和a－1是一个正数?的两个平方根，

∴(2a－1)+(a－1)=0，

解得：，

∴．

故答案为：．

7．（2020·盐池县第五中学初一期中）一个正数的平方根是和，则的值为_______．

【答案】-1

【解析】解：∵一个正数的平方根是2x-1和2-x，

∴2x-1+2-x=0，

解得：x=-1．

故答案为：-1．

考点5：算术平方根的非负性质

典例：（2020·湖南渌口初一期中）已知|2a+b|与互为相反数，

（1）求a、b的值；

（2）解关于x的方程：ax2+4b﹣2＝0．

【答案】（1）；（2）x＝±3．

【解析】（1）∵|2a+b|与互为相反数

∴|2a+b|+＝0，

又知|2a+b|≥0，≥0，

∴|2a+b|＝0，＝0，即，

解得：；

（2）由（1）a＝2，b＝﹣4可知：2x2﹣16﹣2＝0，即x2＝9，

解得：x＝±3．

方法或规律点拨

本题主要考查的是平方根的定义、非负数的性质，熟练掌握平方根的定义、非负数的性质是解题的关键．

巩固练习

1．（2020·安徽濉溪初一期末）若，则=______.

【答案】3

【解析】由题意得：x-2=0，y+1=0，

所以x=2，y=-1，

所以x-y=2-(-1)=3，

故答案为：3.

2．（2020·昆明市官渡区第一中学初一期中）若已知+（y+2）2=0，则(x+y)2019等于_____．

【答案】-1

【解析】解：∵+（y+2）2=0

∴

∴(x+y)2019=-1

故答案为：-1.

3．（2020·四川营山初一期末）若，则 的值为_____．

【答案】1

【解析】解：∵，

∴a+b+5=0，2a-b+1=0，

两式相加得：a=-2，代入a+b+5=0，

解得：b=-3，

∴=1．

故答案为：1．

4．（2020·北京北师大实验中学初一期中）已知，为实数，其中，则__________，________，的算术平方根是_________．

【答案】4    -2    4   

【解析】解：∵，

∴，

解得：x=4，y=-2，

则，

16的算术平方根是4，

故答案为：4；-2，4.

5．（2020·四川马边初三二模）若x，y为实数，且，则 的值为____________

【答案】1

【解析】∵，

∴x-2=0，y+3=0，

解得：x=2，y=-3，

则=（2-3）2020=1．

故答案为：1．

6．（2020·山西交城初一期中）若+|b2﹣1|＝0，则ab＝_____．

【答案】2

【解析】解：∵，

∴，，

∴，，

∴；

故答案为：.

考点6：应用平方根性质解方程

典例：（2020·湖南渌口初一期中）已知|2a+b|与互为相反数，

（1）求a、b的值；

（2）解关于x的方程：ax2+4b﹣2＝0．

【答案】（1）；（2）x＝±3．

【解析】

（1）∵|2a+b|与互为相反数

∴|2a+b|+＝0，

又知|2a+b|≥0，≥0，

∴|2a+b|＝0，＝0，即，

解得：；

（2）由（1）a＝2，b＝﹣4可知：2x2﹣16﹣2＝0，即x2＝9，

解得：x＝±3．

方法或规律点拨

本题主要考查的是平方根的定义、非负数的性质，熟练掌握平方根的定义、非负数的性质是解题的关键．

巩固练习

1．（2020·枣阳市吴店镇清潭第一中学初一期末）若，则________.

【答案】5或；

【解析】∵，

即x−2=±3，

故x=5或−1；

故答案为：5或−1.

2．（2020·宁津县育新中学）求下列各式中x的值：

4(x＋1)2－9＝0；  .

【答案】x＝或x＝；

【解析】解：（1）4(x＋1)2－9＝0,

4(x＋1)2＝9，

(x＋1)2＝，

x＋1＝±，

x＝或x＝－ ．

3．（2019·肇庆学院附属中学）解方程：25x2﹣36＝0．

【答案】x＝±.

【解析】整理得，x2＝，

∴x＝±．

故答案为x＝±．

4．（2020·西宁市海湖中学初一月考）(x＋2)2－36=0；

【答案】，

【解析】解：∵，

∴，

∴，；

5．（2020·广西防城港初一期中）求x的值：(x﹣1)2﹣25=0

【答案】x=6或 x=﹣4

【解析】

【详解】(x﹣1)2﹣25=0，

(x﹣1)2=25，

x-1=±5，

所以x=6或 x=﹣4.

考点7：利用平方根解决实际问题

典例：（2019·山西灵石初二期中）交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度，所用的经验公式是v=16 ，其中v表示车速（单位：km/h），d表示刹车后车轮滑过的距离（单位：m），f表示摩擦因数．在某次交通事故中，测得d=6m，f=1.5，求肇事汽车的车速．

【答案】肇事汽车的车速为48千米/时

【解析】∵d=6，f=1.5，

∴v=16=16×3=48（千米/时），

答：肇事汽车的车速为48千米/时．

方法或规律点拨

本题主要考查了算术平方根在实际中的应用，正确理解题意是解题的关键．

巩固练习

1．（2020·高阳县三利中学初一期末）如图，长方形内有两个相邻的正方形，面积分别为4和9，那么图中阴影部分的面积为（　　）

A．1 B．2 C．3 D．4

【答案】B

【解析】解：设两个正方形的边长是x、y（x＜y），

则x2=4，y2=9，

x=2，y=3，

则阴影部分的面积是（y﹣x）x=（3﹣2）×2=2，

故选B．

2．（2019·汉中市南郑区红庙镇初级中学初一期中）如图，嘉淇把一张边长为的正方形硬纸板的四周各剪去一个同样大小的正方形，再折成一个无盖的长方体盒子，若要求长方体的底面面积为，则剪去的正方形边长为(      )

A． B． C． D．或

【答案】A

【解析】解：设剪去的正方形边长为xcm，

则由题意可得：，

则或（舍去）

∴x=2，

故答案为：A．

3．（2020·北京市第十三中学分校初一期中）物体自由下落的高度h（单位：m）与下落时间t（单位：s）的关系式是．在一次实验中，一个物体从高的建筑物上自由下落，到达地面需要的时间为________s．

【答案】10

【解析】解：把代入中，

得，

∴．

．

故答案为：10．

4．（2020·湖北省武汉市外国语学校美加分校初一期中）一个棱长为8cm的正方体容器装满水，现将这个容器中的水倒入一个高度为的圆柱形玻璃杯中，恰好装满，则这个圆柱形玻璃杯的底面半径为______cm．

【答案】4

【解析】解：设这个圆柱形玻璃杯的底面半径为rcm，

依题意可得：，

∴，

，

∴r取正值4；

故答案为：4．

5．（2020·福建福州初一期末）已知足球场的形状是一个长方形，而国际标准球场的长度和宽度（单位：米）的取值范围分别是，．若某球场的宽与长的比是1：1.5，面积为7350平方米，请判断该球场是否符合国际标准球场的长宽标准，并说明理由．

【答案】符合，理由见解析

【解析】解：符合，理由如下：

设宽为b米，则长为1.5b米，由题意得，

1.5b×b=7350，

∴b=70，或b=-70（舍去），

即宽为70米，长为1.5×70=105米，

∵100≤105≤110，64≤70≤75，

∴符合国际标准球场的长宽标准．

6．（2019·吉林磐石初一期中）如图，一根细线上端固定，下端系一个小球，让这个小球来回自由摆动，来回摆动一次所用的时间（单位：）与细线的长度（单位：）之间满足关系，当细线的长度为时，小球来回摆动一次所用的时间是多少？（结果保留小数点后一位）

【答案】1.3

【解析】把l=0.4m代入关系式得，

∴=1.3（秒）．

7．（2019·江苏南通初一月考）宇宙飞船离开轨道正常运行时，它的速度要大于第一宇宙谏度（单位：m/s）小于第二宇宙速度（单位：m/s），其中的大小满足其中是物理中的一个常数（重力加速度），R是地球半径，请你求出的近似值．

【答案】8×103m/s

【解析】

∵v12=gr，g≈10m/s2，R≈m，∴v1≈=8×103m/s．