




- 函数专题:函数不等式恒成立与能成立问题-【题型分类归纳】2022-2023学年高一数学上学期同步讲与练(人教A版2019必修第一册) 试卷 0 次下载
- 函数专题:利用函数单调性与奇偶性解不等式的6种常见考法-【题型分类归纳】2022-2023学年高一数学上学期同步讲与练(人教A版2019必修第一册) 试卷 0 次下载
- 3.1.2 函数的表示法-【题型分类归纳】2022-2023学年高一数学上学期同步讲与练(人教A版2019必修第一册) 试卷 0 次下载
- 3.2.1 单调性与最大(小)值-【题型分类归纳】2022-2023学年高一数学上学期同步讲与练(人教A版2019必修第一册) 试卷 0 次下载
- 3.2.2 奇偶性-【题型分类归纳】2022-2023学年高一数学上学期同步讲与练(人教A版2019必修第一册) 试卷 0 次下载
人教A版 (2019)必修 第一册3.1 函数的概念及其表示课后作业题
展开3.1.1 函数的概念
一、函数的定义及概念概念
1、函数的定义:设A,B是两个非空数集,
如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,
在集合B中都有唯一确定的数f(x)和它对应,
称f:A→B为从集合A到集合B的一个函数,记作:y=f(x),x∈A
【注意】函数的本质含义:定义域内的任意一个x值,必须有且仅有唯一的y值与之对应。
(1)特殊性:定义的集合A,B必须是两个非空数集;
(2)任意性:A中任意一个数都要考虑到;
(3)唯一性:每一个自变量都在B中有唯一的值与之对应;
(4)方向性:A→B
2、函数的有关概念
(1)函数的定义域、值域:
在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;
与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
(2)函数的三要素:定义域、对应关系和值域.
(3)函数的表示法:表示函数的常用方法有解析法、图象法和列表法.
3、同一个函数
两个函数定义域相同,对应关系相同,则称为同一个函数。
二、区间及相关概念
1、一般区间的表示:设a,b是两个实数,而且a<b,我们规定:这里的实数叫做区间的端点.
在用区间表示连续的数集时,包含端点的那一端用中括号表示,不包含端点的那一端用小括号表示.
定义 | 名称 | 符号 | 数轴表示 |
| 闭区间 |
|
|
| 开区间 |
|
|
| 半开半闭区间 |
|
|
| 半开半闭区间 |
|
|
2、实数集R
可以用区间表示为(-∞,+∞),“∞”读作“无穷大”,
“-∞”读作“负无穷大”,“+∞”读作“正无穷大”.
3、特殊区间的表示
定义 | 符号 | 数轴表示 |
|
|
|
≥ |
|
|
|
|
|
≤ |
|
|
三、求函数的定义域的依据
函数的定义域是指使函数有意义的自变量的取值范围
1、分式的分母不能为零.
2、偶次方根的被开方数的被开方数必须大于等于零,即中
奇次方根的被开方数取全体实数,即中,.
3、零次幂的底数不能为零,即中.
4、如果函数是一些简单函数通过四则运算复合而成的,那么它的定义域是各个简单简单函数定义域的交集。
【注意】定义域用集合或区间表示,若用区间表示熟记,不能用“或”连接,而应用并集符号“∪”连接。
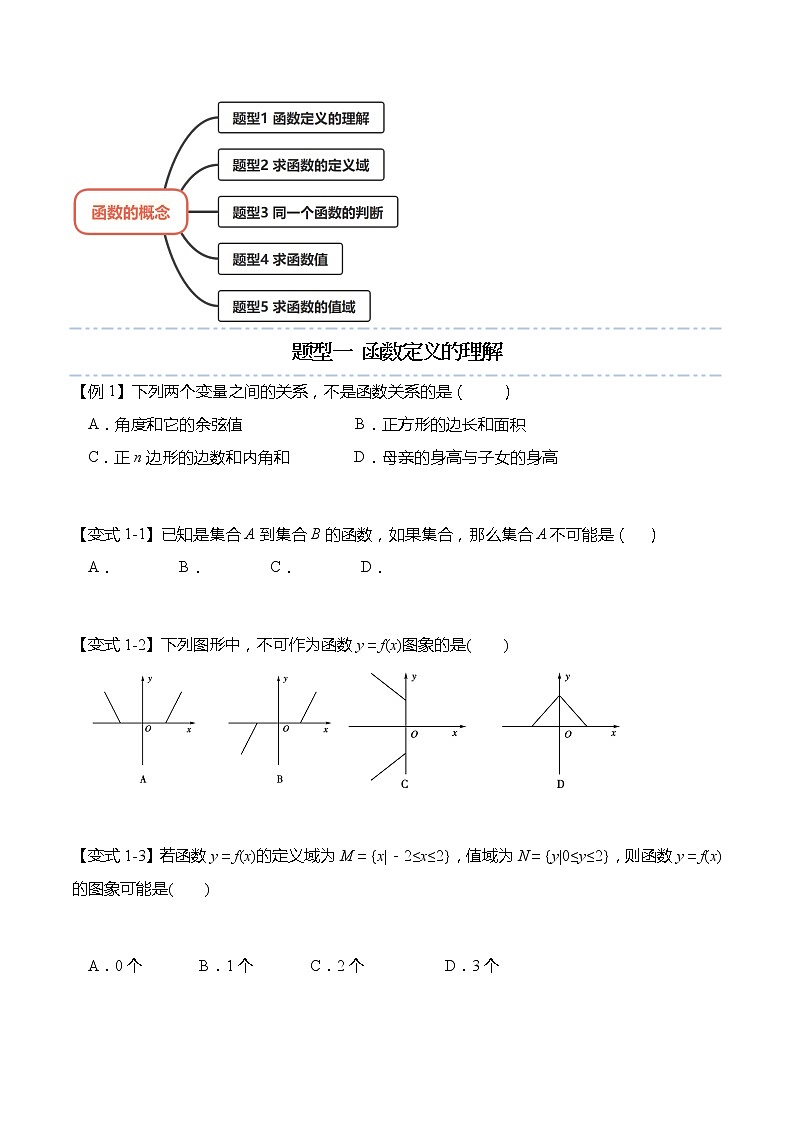
题型一 函数定义的理解
【例1】下列两个变量之间的关系,不是函数关系的是( )
A.角度和它的余弦值 B.正方形的边长和面积
C.正n边形的边数和内角和 D.母亲的身高与子女的身高
【答案】D
【解析】A中的任意一个角总对应唯一的一个余弦值,是函数关系;
B中任意一个正方形的边长总对应唯一的一个面积,是函数关系;
C中任意的正边形边数总对应唯一的顶点角度之和,是函数关系;
D中母亲的身高与子女的身高也不是一一对应的关系,故而不是函数关系。
【变式1-1】已知是集合A到集合B的函数,如果集合,那么集合A不可能是( )
A. B. C. D.
【答案】C
【解析】若集合,则,但,故选:C.
【变式1-2】下列图形中,不可作为函数y=f(x)图象的是( )
【答案】C
【解析】选项C中,x=0时,有2个y值与之对应,不满足函数概念,故选C.
【变式1-3】若函数y=f(x)的定义域为M={x|-2≤x≤2},值域为N={y|0≤y≤2},则函数y=f(x)的图象可能是( )
A.0个 B.1个 C.2个 D.3个
【答案】 B
【解析】A中函数的定义域不是[-2,2],
C中图象不表示函数,D中函数值域不是[0,2],故选B.
【变式1-4】下列对应中:
(1),其中,;
(2),其中,,;
(3),其中y为不大于x的最大整数,,;
(4),其中,,.
其中,是函数的是( )
A.(1)(2) B.(1)(3) C.(2)(3) D.(3)(4)
【答案】B
【解析】(1),其中,;
满足函数的定义,(1)正确;
(2),其中,,,
不满足一个自变量有唯一一个实数y与之对应,
例如当时,;不满足函数的定义,(2)不正确;
(3),其中y为不大于x的最大整数,,;满足函数的定义,③正确;
(4),其中,,,
当时,对应的,(4)不正确.
题型二 求函数的定义域
【例2】已知函数与x的值对应如下表,
x | 1 | 2 | 3 | 4 | 5 | 6 |
| 5 | 10 | 15 | 20 | 25 | 30 |
那么函数的定义域为( )
A. B. C. D.
【答案】A
【解析】由题意知:函数的定义域为.故选:A.
【变式2-1】函数的定义域为( )
A. B. C. D.
【答案】C
【解析】要使函数有意义,
则有,解得且,
所以其定义域为.故选:C.
【变式2-2】函数的定义域是,则函数的定义域为( )
A. B. C. D.
【答案】C
【解析】的定义域是,
得,故或,
所以函数的定义域为.故选:C.
【变式2-3】已知函数的定义域为,则的定义域为( )
A. B. C. D.
【答案】A
【解析】∵函数的定义域为,
∴,则,
即的定义域为,
由,得,
∴的定义域是,故选:A
【变式2-4】已知函数的定义域为,则函数的定义域是( )
A. B. C. D.
【答案】D
【解析】由题意得:,解得,
由解得,
故函数的定义域是.故选:D
题型三 同一个函数的判断
【例3】下面各组函数中是同一函数的是( )
A.与
B.与
C.与
D.与
【答案】C
【解析】A.函数的定义域为,,
两个函数的对应法则不相同,不是同一函数,
B.,定义域为,函数的定义域不相同,不是同一函数
C.两个函数的定义域和对应法则相同,是同一函数
D.由得得,
由得或,
两个函数的定义域不相同,不是同一函数,故选:C.
【变式3-1】下列各组函数表示同一函数的是( )
A., B.
C. D.
【答案】B
【解析】对于A:定义域为,,故A错误;
对于B:与定义域相同都为,且函数解析式相同,
故是同一函数,故B正确;
对于C:定义域为,定义域为,定义域不相同,
故不是同一函数,故C错误;
对于D:定义域为,定义域为,定义域不相同,
故不是同一函数,故D错误;故选:B
【变式3-2】下列函数中与函数是同一函数的是( )
A. B. C. D.
【答案】D
【解析】函数的定义域为R.
A:的定义域为,故与函数不是同一函数.故A错误;
B:的定义域为,故与函数不是同一函数.故B错误;
C:的定义域为R,但是,
故与函数不是同一函数.故C错误;
D:的定义域为R,且,
故与函数是同一函数.故D正确.
【变式3-3】下列函数中,与函数是同一个函数的是( )
A. B. C. D.
【答案】B
【解析】的定义域为;
对于A,定义域为,
与定义域不同,不是同一函数,A错误;
对于B,,与定义域相同,解析式相同,是同一函数,B正确;
对于C,定义域为,与定义域不同,不是同一函数,C错误;
对于D,,
与解析式不同,不是同一函数,D错误.
题型四 求函数值
【例4】已知函数,则( )
A. B. C. D.
【答案】B
【解析】函数,所以.故选:B
【变式4-1】已知函数,则的值是( ).
A. B.0 C.1 D.20
【答案】B
【解析】,
则故选:B
【变式4-2】已知函数,则等于( )
A. B. C. D.0
【答案】D
【解析】由题意,函数,
令,解得,
令,可得.故选:D.
【变式4-3】已知定义在上的函数满足,则( )
A. B. C. D.
【答案】B
【解析】∵,
∴当时,,①,
当时,,②,
,得,解得.故选:B.
【变式4-4】已知,若,则( )
A.3 B.-3 C.-2 D.-1
【答案】D
【解析】,
.故选:D
【变式4-5】,则( )
A. B.2 C. D.3
【答案】D
【解析】,故选:D
【变式4-6】已知,,求:
(1);
(2);
(3).
【答案】(1)-23;-1; (2)-20;-51; (3)8x2-46x+40;4x2-6x-55
【解析】(1)=2×22-3×2-25=-23;=2×2-5=-1;
(2)=f(-1)=2×(-1)2-3×(-1)-25=-20;
=g(-23)=2×(-23)-5=-51;
(3)=f(2x-5)=2×(2x-5)2-3×(2x-5)-25=8x2-46x+40;
=g(2x2-3x-25)=2×(2x2-3x-25)-5=4x2-6x-55.
题型五 求函数的值域
【例5】函数y=x2-4x+6,x∈[1,5)的值域是( )
A.[2,11) B.[3,11) C.[1,11) D.[2,11]
【答案】A
【解析】,
,且函数的对称轴是直线,
∴函数的值域是.故选:A.
【变式5-1】函数值域是( )
A. B. C. D.
【答案】D
【解析】因为,所以,故选:D
【变式5-2】函数的值域是( )
A. B. C. D.
【答案】C
【解析】,
从而可知函数的值域为.故选:C
【变式5-3】函数的值域为( )
A. B. C. D.
【答案】D
【解析】函数的定义域是,
令,则, ,
所以,
因为,所以,
所以原函数的值域为.故选:D.
高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示课后作业题: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000267_t7/?tag_id=28" target="_blank">3.1 函数的概念及其表示课后作业题</a>,文件包含311函数的概念8大题型精讲原卷版docx、311函数的概念8大题型精讲解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第三章 函数的概念与性质3.1 函数的概念及其表示当堂达标检测题: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4000267_t7/?tag_id=28" target="_blank">第三章 函数的概念与性质3.1 函数的概念及其表示当堂达标检测题</a>,文件包含311函数的概念8大题型精练原卷版docx、311函数的概念8大题型精练解析版docx等2份试卷配套教学资源,其中试卷共21页, 欢迎下载使用。
必修 第一册4.3 对数当堂检测题: 这是一份必修 第一册4.3 对数当堂检测题,文件包含43对数-题型分类归纳2022-2023学年高一数学上学期同步讲与练人教A版2019必修第一册解析版docx、43对数-题型分类归纳2022-2023学年高一数学上学期同步讲与练人教A版2019必修第一册原卷版docx等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。













