初中数学北师大版八年级上册1 探索勾股定理教学课件ppt

这是一份初中数学北师大版八年级上册1 探索勾股定理教学课件ppt，共23页。PPT课件主要包含了a2＋b2＝c2等内容，欢迎下载使用。

用拼图法验证勾股定理的基本思想：构造一个图形，利用两种方法计算该图的_________，从而得到一个关于三边长a，b，c之间的等式．练习：如图，小正方形的面积可以表示为____，又可以表示为________________________________________，由此可得等量关系___________________________，整理后可得________________．
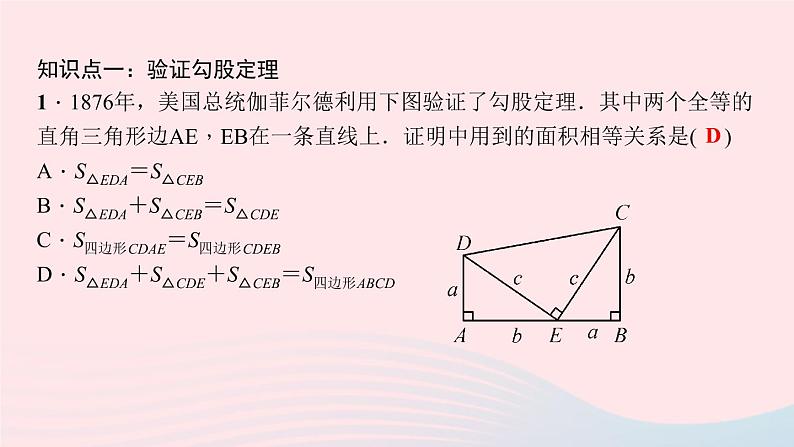
知识点一：验证勾股定理1．1876年，美国总统伽菲尔德利用下图验证了勾股定理．其中两个全等的直角三角形边AE，EB在一条直线上．证明中用到的面积相等关系是( )A．S△EDA＝S△CEBB．S△EDA＋S△CEB＝S△CDEC．S四边形CDAE＝S四边形CDEBD．S△EDA＋S△CDE＋S△CEB＝S四边形ABCD
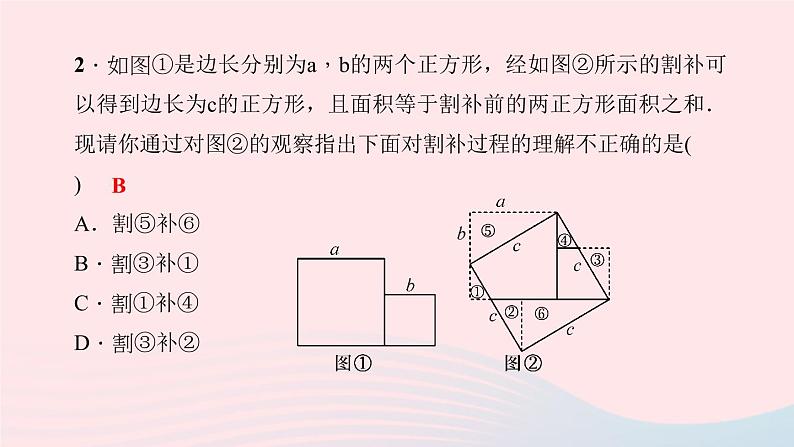
2．如图①是边长分别为a，b的两个正方形，经如图②所示的割补可以得到边长为c的正方形，且面积等于割补前的两正方形面积之和．现请你通过对图②的观察指出下面对割补过程的理解不正确的是( )A．割⑤补⑥B．割③补①C．割①补④D．割③补②
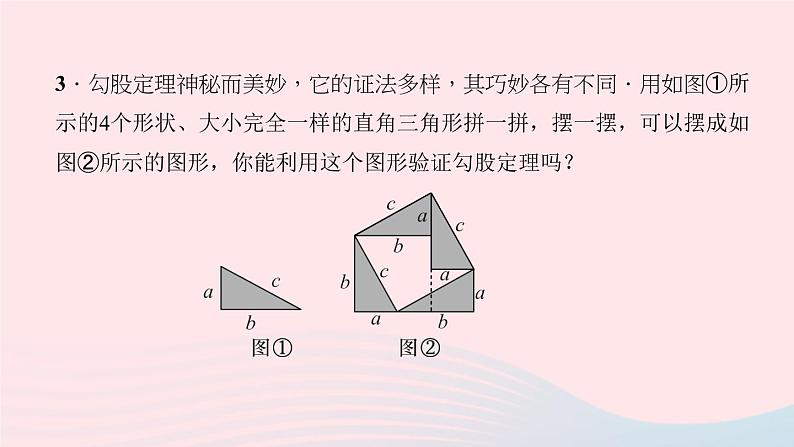
3．勾股定理神秘而美妙，它的证法多样，其巧妙各有不同．用如图①所示的4个形状、大小完全一样的直角三角形拼一拼，摆一摆，可以摆成如图②所示的图形，你能利用这个图形验证勾股定理吗？
知识点二：勾股定理的简单应用4．如图，在△ABC中，AB＝AC＝5，BC＝6，点E，F是中线AD上的两点，则图中阴影部分的面积是( )A．6　　　　B．12　 　 　C．24　 　 　D．30
5．如图所示是一段楼梯，高BC是3 m，斜边AB是5 m，如果在楼梯上铺地毯，那么地毯的长至少需要( )A．5 m B．6 m C．7 m D．8 m
6．如图，一个透明的圆柱形的玻璃杯，测得其内部底面半径为3 cm，高为8 cm，现有一支12 cm的吸管任意斜放于杯中，若不考虑吸管的粗细，吸管露出杯口长度最少为____cm.
7．如图，小李准备建一个蔬菜大棚，棚宽4 m，高3 m，长20 m，棚的斜面用塑料薄膜遮盖，不计墙的厚度，请你帮他计算阳光透过的最大面积．
解：在直角三角形中，由勾股定理可得，直角三角形的斜边长为5 m，所以长方形塑料薄膜的面积是5×20＝100(m2)．即阳光透过的最大面积是100 m2
8．(2017·正定模拟)如图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC＝6，BC＝5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长是( )A．52 B．42 C．76 D．72
9．如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为( )A．4 B．6 C．16 D．55
10．如图，隔湖有两点A，B，从与BA方向成直角的BC方向上的点C测得CA＝50米，CB＝40米，求：(1)A，B两点间的距离；(2)点B到直线AC的距离．
11．如图，有一张直角三角形纸片，两直角边AC＝6 cm，BC＝8 cm，将△ABC折叠，使点B与点A重合，折痕为DE，求CD的长．
12．如图，为了丰富少年儿童的业余文化生活，某社区要在AB所在的直线上建一图书阅览室．该社区有两所学校，所在的位置在点C和点D处，CA⊥AB于点A，DB⊥AB于点B.已知AB＝25 km，CA＝15 km，DB＝10 km.试问：阅览室E建在距点A多少千米处，才能使它到C，D两所学校的距离相等．
解：设阅览室E到点A的距离为x km，连接CE，DE.在Rt△EAC和Rt△EBD中，CE2＝AE2＋AC2＝x2＋152，DE2＝EB2＋DB2＝(25－x)2＋102.∵EC＝ED，∴x2＋152＝(25－x)2＋102，解得x＝10，建在距点A10 km处
13．(阿凡题：1071102)在△ABC中，BC＝a，AC＝b，AB＝c，若∠C＝90°，如图①所示，根据勾股定理，得a2＋b2＝c2；若△ABC不是直角三角形，如图②，图③所示，请你类比勾股定理，试猜想a2＋b2与c2的大小关系，并说明理由．
解：若△ABC是锐角三角形，则有a2＋b2＞c2；若△ABC为钝角三角形(∠ACB为钝角)，则有a2＋b2＜c2.理由如下：(1)当△ABC是锐角三角形时，如图②所示，过点A作AD⊥CB，垂足为D，设CD＝x，则有DB＝a－x.易得b2－x2＝c2－(a－x)2，即b2－x2＝c2－a2＋2ax－x2，化简得a2＋b2＝c2＋2ax.∵a＞0，x＞0，∴2ax＞0，∴a2＋b2＞c2