高中数学人教A版 (2019)必修 第一册4.4 对数函数背景图ppt课件

这是一份高中数学人教A版 (2019)必修 第一册4.4 对数函数背景图ppt课件，文件包含442对数函数的图象和性质一pptx、442对数函数的图象和性质一docx等2份课件配套教学资源，其中PPT共60页， 欢迎下载使用。


4.4.2　对数函数的图象和性质(一)
第四章　 §4.4　对数函数
学习目标
1.初步掌握对数函数的图象和性质.
2.会类比指数函数研究对数函数的性质.
3.掌握对数函数的图象和性质的简单应用.
导语
同学们，还记得我们是如何研究指数函数的吗？实际上，研究对数函数的思路和研究指数函数的思路是一致的，我们可以用类比的方法来研究对数函数.请同学们看下面的问题1.
内容索引
对数函数的图象和性质

一
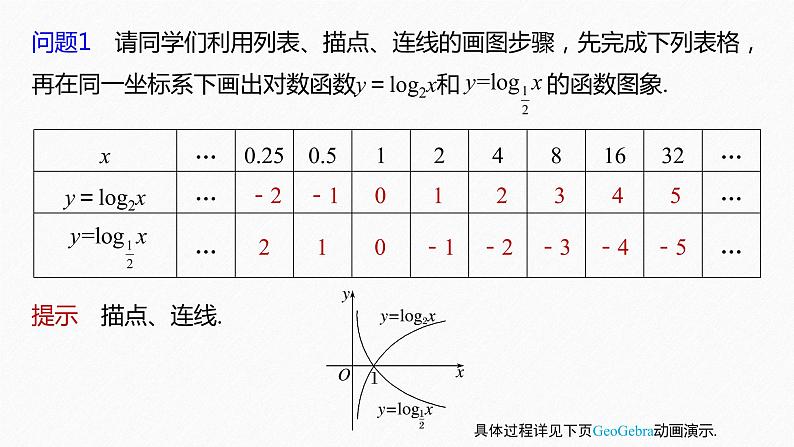
问题1　请同学们利用列表、描点、连线的画图步骤，先完成下列表格，再在同一坐标系下画出对数函数y＝log2x和 的函数图象.
提示　描点、连线.
－2　－1　 0　 1　 2 　 3　 4 　5
2　 1　 0　 －1 －2 －3 －4　－5
具体过程详见下页GeoGebra动画演示.
问题2　通过观察函数y＝log2x和 的图象，分析性质，并完成下表：
x∈(0，＋∞)
x∈(0，＋∞)
增函数
减函数
无最值
无最值
R
R
非奇非偶函数
非奇非偶函数
(1,0)
(1,0)
y<0
y>0
y>0
y<0
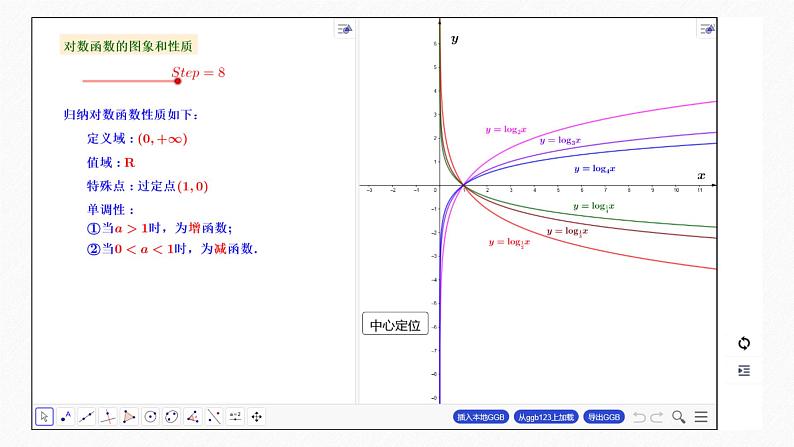
问题3　为了更好地研究对数函数的性质，我们再选取底数a＝3,4, 你能在同一坐标系下作出它们的函数图象吗？
提示　
知识梳理
对数函数的图象和性质
(0，＋∞)
无最大、最小值
非奇非偶函数
(1,0)
(－∞，0)
[0，＋∞)
(0，＋∞)
(－∞,0]
x轴
(1)函数图象只出现在y轴右侧.(2)对任意底数a，当x＝1时，y＝0，故过定点(1,0).(3)当01时，底数越大，图象越靠近x轴.(5)任意底数互为倒数的两个对数函数的图象关于x轴对称.
注意点：
(1)如图，若C1，C2分别为函数y＝logax和y＝logbx的图象，则A.0b>1D.b>a>1
作直线y＝1，则直线与C1，C2的交点的横坐标分别为a，b，易知0√
(2)若函数y＝loga(x＋b)＋c(a>0，且a≠1)的图象恒过定点(3,2)，则实数b＝____，c＝_____.
∵函数的图象恒过定点(3,2)，∴将(3,2)代入y＝loga(x＋b)＋c，得2＝loga(3＋b)＋c.又当a>0，且a≠1时，loga1＝0恒成立，∴c＝2,3＋b＝1，∴b＝－2，c＝2.
－2 　2
(3)已知f(x)＝loga|x|(a>0，且a≠1)满足f(－5)＝1，试画出函数f(x)的图象.
因为f(－5)＝1，所以loga5＝1，即a＝5，
所以函数f(x)＝log5|x|的图象如图所示.
延伸探究1.在本例中，若条件不变，试画出函数g(x)＝loga|x－1|的图象.
因为f(x)＝log5|x|，所以g(x)＝log5|x－1|，如图，g(x)的图象是由f(x)的图象向右平移1个单位长度得到的.
2.在本例中，若条件不变，试画出函数h(x)＝|logax|的图象.
因为a＝5，所以h(x)＝|log5x|.h(x)的图象如图中实线部分所示.
对数型函数图象的变换方法(1)作y＝f(|x|)的图象时，保留y＝f(x)(x>0)的图象不变，x<0时y＝f(|x|)的图象与y＝f(x)(x>0)的图象关于y轴对称.(2)作y＝|f(x)|的图象时，保留y＝f(x)的x轴及上方图象不变，把x轴下方图象以x轴为对称轴翻折上去即可.(3)有关对数函数平移也符合“左加右减，上加下减”的规律.(4)y＝f(－x)与y＝f(x)关于y轴对称，y＝－f(x)与y＝f(x)关于x轴对称，y＝－f(－x)与y＝f(x)关于原点对称.
反思感悟
(1)函数f(x)＝loga|x|＋1(a>1)的图象大致为
√
∵函数f(x)＝loga|x|＋1(a>1)是偶函数，∴f(x)的图象关于y轴对称，当x>0时，f(x)＝logax＋1单调递增；当x<0时，f(x)＝loga(－x)＋1单调递减，又∵图象过(1,1)，(－1,1)两点，结合选项可知选C.
(2)画出函数y＝|log2(x＋1)|的图象，并写出函数的值域及单调区间.
函数y＝|log2(x＋1)|的图象如图所示.由图象知，其值域为[0，＋∞)，单调递减区间是(－1,0]，单调递增区间是(0，＋∞).
利用单调性比较对数值的大小

二
　　比较下列各组中两个值的大小：(1)log31.9，log32；
因为y＝log3x在(0，＋∞)上单调递增，1.9<2，所以log31.9(2)log23，log0.32；
因为log23>log21＝0，log0.32log0.32.
(3)logaπ，loga3.14(a>0，且a≠1)；
当a>1时，函数y＝logax在(0，＋∞)上单调递增，则有logaπ>loga3.14；当01时，logaπ>loga3.14；当0(4)log50.4，log60.4.
在同一直角坐标系中，作出y＝log5x，y＝log6x的图象，再作出直线x＝0.4(图略)，观察图象可得log50.4比较对数值大小时常用的四种方法(1)同底数的利用对数函数的单调性.(2)同真数的利用对数函数的图象或用换底公式转化.(3)底数和真数都不同，找中间量.(4)若底数为同一参数，则根据底数对对数函数单调性的影响，对底数进行分类讨论.
反思感悟
　　　 比较大小：(1)loga5.1，loga5.9(a>0，且a≠1)；
当a>1时，y＝logax在(0，＋∞)上是增函数，又5.1<5.9，所以loga5.1loga5.9.综上，当a>1时，loga5.1loga5.9.
利用单调性解对数不等式

三
　　解下列关于x的不等式：(1)　　　　　　　 ；
所以原不等式的解集为{x|0(2)loga(2x－5)>loga(x－1)；
综上所述，当a>1时，原不等式的解集为{x|x>4}；
对数不等式的三种考查类型及解法(1)形如logax>logab的不等式，借助y＝logax的单调性求解，如果a的取值不确定，需分a>1与0b的不等式，应将b化为以a为底数的对数式的形式(b＝logaab)，再借助y＝logax的单调性求解.(3)形如logf(x)a>logg(x)a(f(x)，g(x)>0且不等于1，a>0)的不等式，可利用换底公式化为同底的对数进行求解，或利用函数图象求解.
反思感悟
(1)求满足不等式log3x<1的x的取值集合；
∵log3x<1＝log33，又函数y＝log3x在(0，＋∞)上为增函数，
∴x的取值集合为{x|0(2)已知log0.7(2x)∵函数y＝log0.7x在(0，＋∞)上为减函数，
解得x>1.∴x的取值范围是(1，＋∞).
课堂小结
1.知识清单： (1)对数函数的图象及性质. (2)利用对数函数的图象及性质比较大小. (3)利用单调性解对数不等式.2.方法归纳：分类讨论法、数形结合法.3.常见误区：作对数函数图象时易忽视底数a>1与0随堂演练

1.函数y＝loga(x－1)(01
2
3
4
∵0√
1
2
3
4
2.若a＝20.2，b＝log43.2，c＝log20.5，则A.a>b>c B.b>a>cC.c>a>b D.b>c>a
√
∵a＝20.2>1>b＝log43.2>0>c＝－1，∴a>b>c.
1
2
3
4
3.不等式 的解集为
√
1
2
3
4
4.若 ，则实数a的取值范围是__________________.
当a>1时，满足条件；
课时对点练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1. 函数y＝logax，y＝logbx，y＝logcx，y＝logdx的图象如图所示，则a，b，c，d的大小顺序是A.1√
令函数y＝logax，y＝logbx，y＝logcx，y＝logdx取同样的函数值1，得到的自变量的值恰好分别是a，b，c，d.直线y＝1从左到右依次与上述四个函数的图象交于A(c，1)，B(d，1)，C(a，1)，D(b，1)(图略)，从而得出c1，b>1，d<1，c<1，∴c1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2.若lg(2x－4)≤1，则x的取值范围是A.(－∞，7] B.(2,7]C.[7，＋∞) D.(2，＋∞)
√
由lg(2x－4)≤1，得0<2x－4≤10，即21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3.设a＝log37，b＝21.1，c＝0.83.1，则A.b√
∵a＝log37，∴12.∵c＝0.83.1，∴01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4.函数f(x)＝logax(0√
∵01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5.函数f(x)＝lg(|x|－1)的大致图象是
√
由f(x)的定义域为(－∞，－1)∪(1，＋∞)，且f(－x)＝lg(|－x|－1)＝lg(|x|－1)＝f(x)，得f(x)是偶函数，由此知C，D错误；又当x>1时，f(x)＝lg(x－1)在(1，＋∞)上单调递增，所以B正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6.(多选)已知a>0，b>0，且ab＝1，a≠1，则函数f(x)＝ax与函数g(x)＝－logbx在同一坐标系中的图象可能是
∵g(x)＝－logbx＝　　＝logax，∴f(x)和g(x)的单调性相同，结合选项可知A，B正确.
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.函数y＝loga(x－4)＋2(a>0且a≠1)恒过定点_______.
令x－4＝1得x＝5，此时y＝loga1＋2＝2，所以函数y＝loga(x－4)＋2恒过定点(5,2).
(5,2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.若正实数x，y满足x＋y＝1，则log2x＋log2y的最大值为_____.
－2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.比较下列各组中两个值的大小：(1)ln 0.3，ln 2；
因为函数y＝ln x在(0，＋∞)上是增函数，又0.3<2，所以ln 0.31
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)loga3.1，loga5.2(a>0，且a≠1)；
当a>1时，函数y＝logax在(0，＋∞)上是增函数，又3.1<5.2，所以loga3.1loga5.2.综上所述，当a>1时，loga3.1loga5.2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
即log30.2(3)log30.2，log40.2；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为函数y＝log3x在(0，＋∞)上是增函数，又π>3，所以log3π>log33＝1.同理，1＝logππ>logπ3，所以log3π>logπ3.
(4)log3π，logπ3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.已知f(x)＝|lg x|，且　>a>b>1，试借助图象比较f(a)，f(b)，f(c)的大小.
先作出函数y＝lg x的图象，再将图象位于x轴下方的部分以x轴为对称轴翻折到x轴上方，于是得f(x)＝|lg x|的图象(如图)，由图象可知，f(x)在(0,1)上单调递减，在(1，＋∞)上单调递增.
∴f(c)>f(a)>f(b).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11.已知函数f(x)＝ln x，g(x)＝lg x，h(x)＝log3x，直线y＝a(a<0)与这三个函数的交点的横坐标分别为x1，x2，x3，则x1，x2，x3的大小关系是A.x2√
分别作出这三个函数的大致图象，如图所示.由图可知，x21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12.若函数f(x)＝loga(x＋b)的图象如图所示，其中a，b为常数，则函数g(x)＝ax＋b的图象大致是
由f(x)的图象可知0√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13.设偶函数f(x)＝loga|x－b|在(－∞，0)上单调递增，则f(a＋1)与f(b＋2)的大小关系是A.f(a＋1)f(b＋2)
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为函数f(x)是偶函数，所以b＝0，又函数在(－∞，0)上单调递增，所以函数在(0，＋∞)上单调递减，则0f(b＋2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.已知f(x)是定义在R上的偶函数，且在[0，＋∞)上单调递增， ＝0，则不等式 的解集为__________________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∵f(x)是R上的偶函数，∴它的图象关于y轴对称.∵f(x)在[0，＋∞)上单调递增，∴f(x)在(－∞，0]上单调递减，
∴ 或 ，
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15.已知f(x)＝ 的值域为R，那么实数a的取值范围是________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
要使函数f(x)的值域为R，
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16.若不等式x2－logmx<0在 内恒成立，求实数m的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
由x2－logmx<0，得x21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16