八年级上册第十一章 三角形11.3 多边形及其内角和11.3.2 多边形的内角和教案

<多边形的内角和>教学设计

一、教学目标： 

1．掌握多边形的内角和定理；

    2．运用多边形内角和定理进行有关的计算．

二、教学重难点：

重点：多边形的内角和定理；

难点：内角和定理的推导

三、教法学法设计：

以教师的精讲、点拨引导为主，辅以引导发现、合作交流。

 四、教具、学具准备：

多媒体课件、三角板、量角器。

 五、教学过程： 

（一）复习提问，导入新课 

问题：三角形的内角和是多少度？正方形和长方形的内角和又是多少度？ 【设计说明】直接提出问题，唤醒学生已有的知识，把学生引到本节课思维的最近发展区，为新课学习提供知识铺垫。 

（二）引申思考，探索新知 

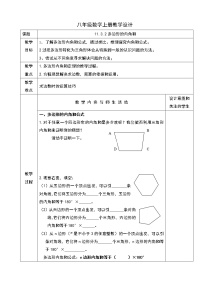
（1）探究活动一：探索四边形内角和。 问题：我们已经知道正方形和长方形的内角和为360°，那么任意四边形的内角和是多少？你是怎么得到的？

①测量法：量出任意一个四边形每个内角度数,然后相加为360° 。

  （让学生明确使用这种做法的缺陷是往往会引起误差，得不到预想的结果）

②拼图法。把四个角拼在一起刚好是一个周角360° 

（让学生明确使用这种做法的局限性，不是任何情况都可以采用这种办法验证四边形的内角和。）

   教师引导：你能利用三角形内角和定理证明你的结论吗？（教师在做法②的基础上引导学生利用作辅助线的方法,连结四边形的对角线,把一个四边形转化为两个三角形，并写出证明过程。 ）            

从四边形的一个顶点出发，可以引_____条对角线，它们将四边形分为_____个三角形，四边形的内角和等于180°×______．

探究活动二：类比前面的过程你能探索五边形和六边形的内角和各是多少吗？

从五边形的一个顶点出发，可以引_____条对角线，

它们将五边形分为_____个三角形，五边形的内角和

等于180°×______．

从六边形的一个顶点出发，可以引_____条对角线，

它们将六边形分为_____个三角形，六边形的内角和等

于180°×______．

探究活动一：你能从四边形、五边形、六边形的内角和的研究过程获得启发，发现多边形的内角和和边数的关系吗？

归纳：一般地，从n边形的一个顶点出发，可以引_________条对角线，它们将n边形分为_________个三角形，n边形的内角和等于                    。

【设计说明】（1）活动一的探究，学生易把四边形分割成 三角形，从而把四边形的内角和与三角形的内角和有效的 联系起来，求出任意四边形的内角和。这个环节着重渗透分割转化的思想方法。为探究n边形的内角和做准备。 

（2）探究活动二：探索五边形、六边形、七边形的内角和 学生先独立思考每个问题再分组讨论。 

关注①学生能否类比四边形的方式解决问题得出正确的结论。     ②学生能否采用不同的方法。

学生分组讨论后进行交流（五边形的内角和） 

 （3） 活动三：探究任意多边形的内角和公式。 

思考： ①多边形内角和与三角形内角和的关系？      ②多边形的边数与内角和的关系？  ③从多边形一个顶点引的对角线分三角形的个数与多边形边数的关系？ 学生结合思考题进行讨论，并把讨论后的结果进行交流。 

得出结论：多边形内角和公式：（n-2）•180º 

   【设计说明】逐步增加图形的复杂性，再一次经历转化的过程，加深对转化的思想方法的理解，体会由简单到复杂、由特殊到复杂的思想方法。 

想一想：把一个多边形分成几个三角形，可以得到多边形的内角和。除利用对角线把多边形分成几个三角形外，还有其他分法吗？以四边形为例。 

学生动手并与同伴交流，老师归纳，多媒体演示。 

【设计说明】让学生再一次经历转化的过程，注意培养学生思维的灵活性，进一步发展学生的推理能力和语言表达能力。 

（三）巩固应用新知 

1．十二边形的内角和是_________；

2.已知多边形的每个内角都是135度,则这个多边形是_______.

3.一个多边形当边数增加1时，它的内角和增加        度。

4.过多边形的一个顶点可以引9条对角线，那么这个多边形的内角和是          。

5.一个多边形的内角和等于900°，它是几边形？

6.求出图形中x的值；

7.想一想：  如果一个四边形的一组对角互补，那么另一组对角有什么关系？

(四）课堂小结 

问题：谈谈本节课你有哪些收获？ 

【设计说明】鼓励学生积极发言，并对学生的进步给予肯定，树立学生学好数学的自信心。再一次发展学生的评理能力和语言表达能力。