初中人教版11.3.2 多边形的内角和教案设计

这是一份初中人教版11.3.2 多边形的内角和教案设计，共4页。教案主要包含了多边形的内角和公式，多边形的外角和等内容，欢迎下载使用。


课题
11.3.2多边形的内角和
教学
目标
了解多边形内角和公式，通过类比、推理探究内角和公式；
2过把多边形转化为三角形体会从特殊到一般的认识问题的方法；
3、尝试从不同角度寻求解决问题的方法；
教学
重点
1.多边形内角和定理的推导过程。
2.方程思想解决求边数，简算的依据和运用。
教学
难点
求边数时的运算技巧
教学
过程
教 学 内 容 与 师 生 活 动
设计意图和
关注的学生
一、多边形的内角和公式
1.对于任意一个四边形它的内角和是多少度呢？我们能否利用三角形内角和来证明你的猜想？
请动手证明一下。




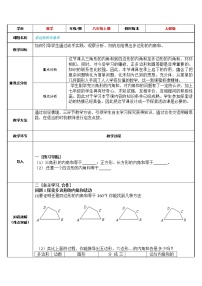
2.观察右图，填空：
（1）从五边形的一个顶点出发，可以引 条对角线，它们将五边形分为 个三角形，五边形的内角和等于180°× 。
（2）从六边形的一个顶点出发，可以引 条对角线，它们将六边形分为 个三角形，六边形的内角和等于180°× 。
（3）从n边形（是不小于3的任意整数）的一个顶点出发，可以引 条对角线，它们将n边形分为 个三角形，n边形的内角和等于180°× 。
多边形内角和公式：n边形内角和等于（ ）×180°

二、多边形的外角和
1.如图， 在六边形的每一个顶点处各取一个外角，
这些外角的和叫做六边形的外角和。
六边形的外角和等于多少度？
分析：
（1）任何一个外角和与它相邻的内角有什关系？
（2）六边形的六个外角加上与它们相邻的内角所得总和是________________
（3）上述总和与六边形的内角和、外角和有什么关系？
解：六边形的外角和=_____________－六边形的内角和
= °－ ° = °
总结：多边形的外角和是
从n边形的一个顶点出发，可以引（n-3）条对角线，它们将n边形分为（n-2）个三角形，n边形的内角和等于180°×（n-2）
简单计算：四边形内角和为 360°
五边形内角和为 540°
六边形内角和为 720°
七边形内角和为900°
八边形内角和为1080°
九边形内角和为1260度
例1：在六边形的每个顶点处各取一个外角，
这些外角的和叫做六边形的外角和，
六边形的外角和等于多少？
多边形的外角和等于3600
证明：N180°-（n-2）180°
= n180°- n180°+360°
=360°
课堂练习
1.十二边形的内角和是 度
2.正六边形的每一个外角等于________，每一个内角等于_______。
3.多边形每一个外角等于36°,则它是 边形，多边形每一个内角都等于120°，则它是 边形。
5.已知一个多边形，它的内角和等于外角和，则它是 形。
6.一个多边形的内角和等于900°，求它的边数。


7.已知在四边形ABCD中，如果∠A：∠B：∠C：∠D=1：2：3：4，
求∠A，∠B，∠C，∠D的度数．


8.一个多边形的各内角都等于120°，它是几边形？
9. 已知一个多边形，它的内角和等于外角和的2倍，求这个多边形的边数？



10. 一个多边形的内角和比它的外角和的3倍少180°，求边数。
板
书
设
计
1.多边形内角和公式：
2. 多边形外角和：
教
学
反
思