人教版八年级下册19.2.2 一次函数单元测试一课一练

新人教版八年级下册第19章 一次函数

单元测试试卷（A卷）

一、选择题 （每题3分，共30分。每题只有一个正确答案，请将正确答案的代号填在下面的表格中）

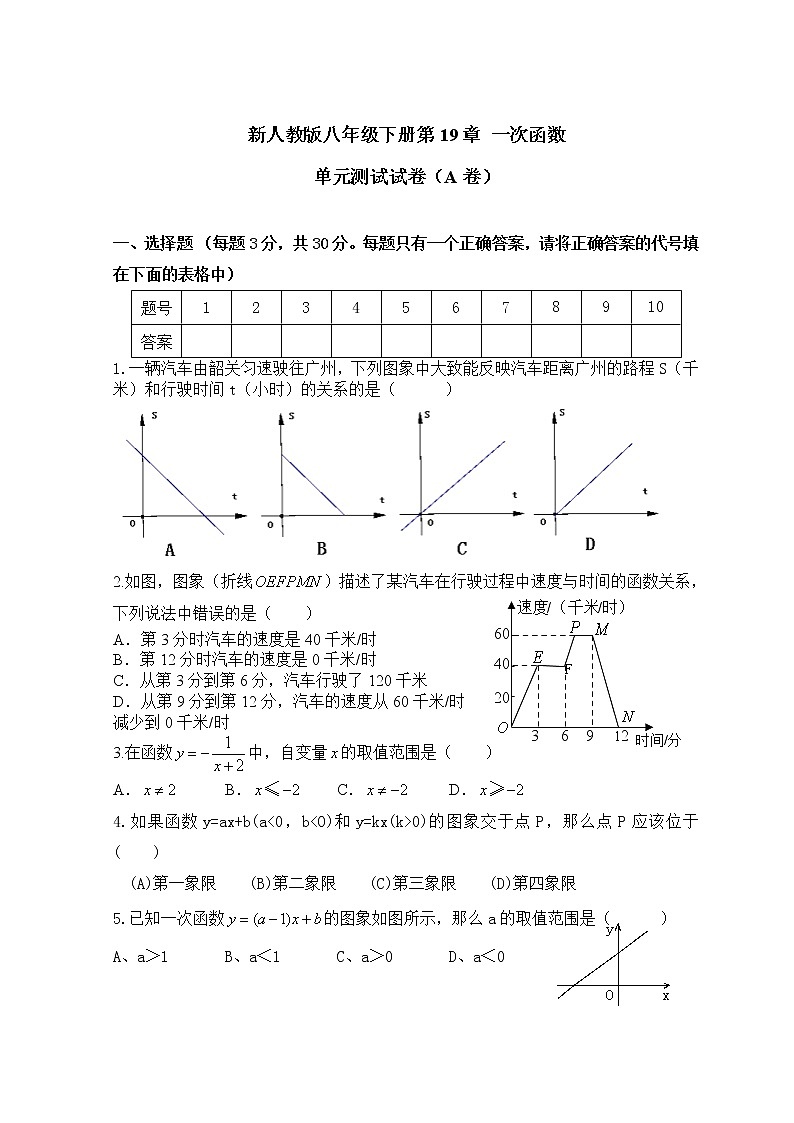
1.一辆汽车由韶关匀速驶往广州，下列图象中大致能反映汽车距离广州的路程S（千米）和行驶时间t（小时）的关系的是（      ）

2.如图，图象（折线）描述了某汽车在行驶过程中速度与时间的函数关系，下列说法中错误的是（    ）

A．第3分时汽车的速度是40千米/时

B．第12分时汽车的速度是0千米/时

C．从第3分到第6分，汽车行驶了120千米

D．从第9分到第12分，汽车的速度从60千米/时

减少到0千米/时

3.在函数中，自变量的取值范围是（    ）

A．  B．  C．  D．

4.如果函数y=ax+b(a<0，b<O)和y=kx(k>0)的图象交于点P，那么点P应该位于(    )

  (A)第一象限    (B)第二象限    (C)第三象限    (D)第四象限

5.已知一次函数的图象如图所示，那么a的取值范围是（      ）

A、a＞1       B、a＜1       C、a＞0       D、a＜0

6.函数y＝＋中自变量x的取值范围是(      )

A．x≤2         B．x＝3      C． x＜2且x≠3        D．x≤2且x≠3

7．已知一次函数的图象与直线y=-x+1平行，且过点（8，2），那么此一次函数的解析式为（     ）

A．      B．        C．       D．

 8.下列四个点中，有三个点在同一条直线上，不在这条直线上的点是（    ）

A．  B．  C．  D．

9.如果一次函数的图象经过第一象限，且与轴负半轴相交，那么（    ）

A．， B．， C．， D．，

10. 2007年我国铁路进行了第六次大提速，一列火车由甲市匀速驶往相距600千米的乙市，火车的速度是200千米/小时，火车离乙市的距离（单位：千米）随行驶时间（单位：小时）变化的函数关系用图象表示正确的是（    ）

二、填空题（每题3分，共30）

11.已知一次函数的图象经过点，，则       ，       ．

12.函数的自变量的取值范围是       ．

13.某函数的图象经过（1、-1），且函数y的值随自变量的值增大而增大，请你写出一个符合上述条件的函数关系式：                         

14.若正比例函数（≠）经过点（，），则该正比例函数的解析式为__              _____。

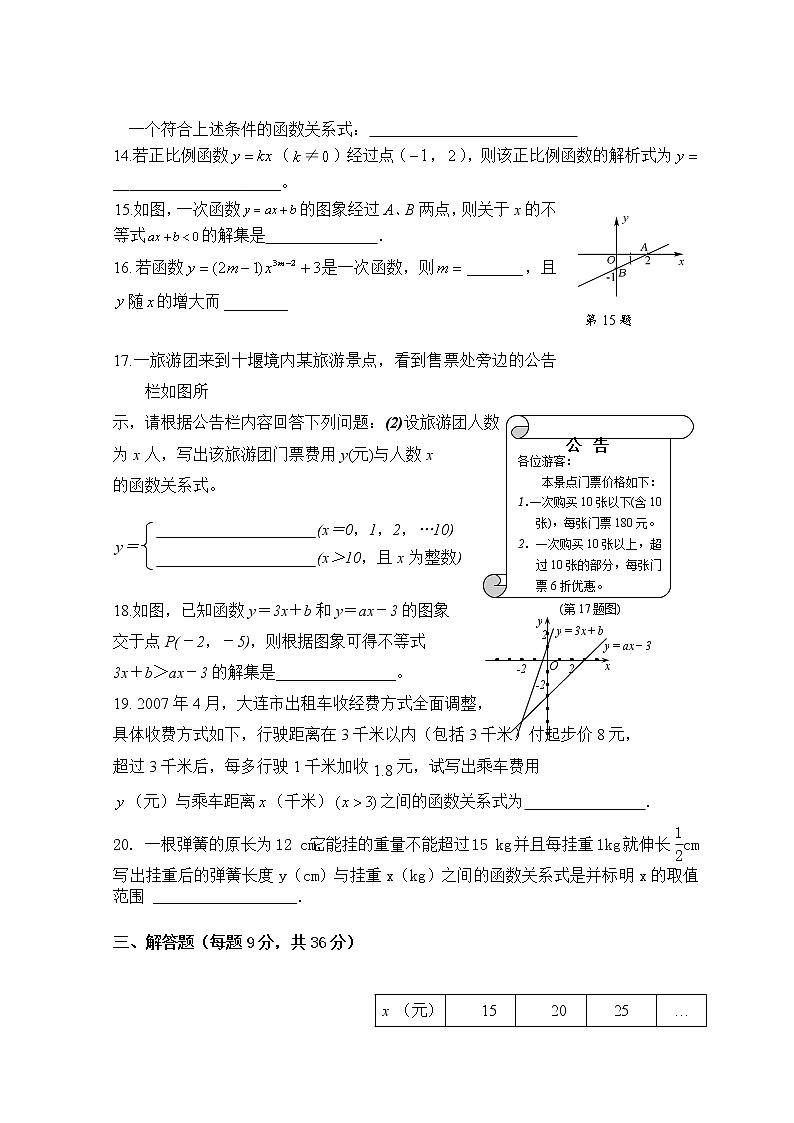
15.如图，一次函数的图象经过A、B两点，则关于x的不等式的解集是              ．   

16.若函数是一次函数，则，且随的增大而

17.一旅游团来到十堰境内某旅游景点，看到售票处旁边的公告栏如图所

示，请根据公告栏内容回答下列问题：(2)设旅游团人数

为x人，写出该旅游团门票费用y(元)与人数x

的函数关系式。

18.如图，已知函数y＝3x＋b和y＝ax－3的图象

交于点P(－2，－5)，则根据图象可得不等式

3x＋b＞ax－3的解集是_______________。

19. 2007年4月，大连市出租车收经费方式全面调整，

具体收费方式如下，行驶距离在3千米以内（包括3千米）付起步价8元，

超过3千米后，每多行驶1千米加收1.8元，试写出乘车费用

（元）与乘车距离（千米）之间的函数关系式为              　 ．

20. 一根弹簧的原长为12 cm，它能挂的重量不能超过15 kg并且每挂重1kg就伸长cm写出挂重后的弹簧长度y（cm）与挂重x（kg）之间的函数关系式是并标明x的取值范围 __________________．

三、解答题（每题9分，共36分）

 21．某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：

若日销售量y是销售价x的一次函数．

（1）求出日销售量y（件）与销售价x（元）的函数关系式；

（2）求销售价定为30元时，每日的销售利润．

22.画出函数y=2x+6的图象，利用图象：（1）求方程2x+6=0的解；（2）求不等式的解；（3）若，求x的取值范围。

23.在市区内，我市乘坐出租车的价格（元）与路程（km）的函数

关系图象如图6所示．（1）请你根据图象写出两条信息；（2）小明从

学校出发乘坐出租车回家用了13元，求学校离小明家的路程．

24．某单位需要用车，准备和一个体车主或一国有出租公司其中的一家签订合同，设汽车每月行驶xkm，应付给个体车主的月租费是y1元，付给出租车公司的月租费是y2元，y1，y2分别与x之间的函数关系图象是如图11-3-4所示的两条直线，观察图象，回答下列问题：

（1）每月行驶的路程在什么范围内时，租国有出租车公司的出租车合算？

（2）每月行驶的路程等于多少时，租两家车的费用相同？

（3）如果这个单位估计每月行驶的路程为2300km，那么这个单位租哪家的车合算？

四、解答题（每题10分，共30分）

25.某电信公司开设了甲、乙两种市内移动通信业务。甲种使用者每月需缴15元月租费，然后每通话1分钟, 再付话费0.3元； 乙种使用者不缴月租费, 每通话1分钟, 付话费0.6元。若一个月内通话时间为x分钟, 甲、乙两种的费用分别为y1和y2元。

(1)试分别写出y1、y2与x之间的函数关系式；

(2)在同一坐标系中画出y1、y2的图像；

(3)根据一个月通话时间，你认为选用哪种通信业务更优惠？

26. 某地区的电力资源丰富，并且得到了较好的开发.该地区一家供电公司为了鼓励居民用电，采用分段计费的方法来计算电费.月用电量x（度）与相应电费y（元）之间的函数图像如图所示.

⑴月用电量为100度时，应交电费         元；

⑵ 当x≥100时，求y与x之间的函数关系式；

⑶ 月用电量为260度时，应交电费多少元？

科

27.某农户种植一种经济作物，总用水量（米）与种植时间（天）之间的函数系式如图所示．

网⑴ 第天的总用水量为多少米？

⑵ 当时，求与之间的函数关系式．

⑶ 种植时间为多少天时，总用水量达到7000米？

五、解答题（每题12分，共24分）

28、如图信息，为走私船，为我公安快艇，航行时路程与时间的函数图象，问

（1）在刚出发时我公安快艇距走私船多少㎞？

（2）计算走私船与公安快艇的速度分别是多少？

（3）写出, 的解析式.

（4）问6分钟时两艇相距几海里。

（5）猜想，公安快艇能否追上走私船，

若能追上，那么在几分钟追上？

29.某校八年级举行英语演讲比赛，排了两位老师去学校附近的超市购买笔记本作为奖品．经过了解得知，该超市的A、B两种笔记本的价格分别是12元和8元，他们准备购买者两种笔记本共30本．

(1)如果他们计划用300元购买奖品，那么能卖这两种笔记本各多少本?

(2)两位老师根据演讲比赛的设奖情况，决定所购买的A种笔记本的数量要少于B种笔记本数量的，但又不少于B种笔记本数量的，如果设他们买A种笔记本n本，买这两种笔记本共花费w元．

①请写出w（元）关于n（本）的函数关系式，并求出自变量n的取值范围；

②请你帮助他们计算，购买这两种笔记本各多少时，花费最少，此时的花费是多少元？

参考答案

一、1－5   BCCCA   6－10 AVDBD

二、11. -2  12. x≠4  13. y=2x-3等（答案不唯一）。  14. -2x   15. x＜2   16.m=1  增大

17. 180x  108x+720   18.x﹥-2    19.y=1.8x+2.6   20. y=12+x (0≤x≤15)

三、

21.（1）y=-x+40  (2)200元

22.画图略（1）x=-3   (2)x>-3  (3)-≤x≤-

23.(1)略 （2）7km

24.（1）1500km以内。（2）1500km (3)租个体车主的车合算。

25.（1）y1=15+0.3x   y2=0.6x(2)略（3）当通话时间小于50分钟时，选乙，当通话时间大于50分钟时，选甲，当通话时间等于50分种时，选甲乙都可。

26.（1）60（2）y=x+10(3)140元

27.（1）100m3(2)y=300x-5000(3)40天

28.（1）5km (2) 1海里/分  1.5海里/分。  （3）l1=t+5  l2=1.5t

(4)2海里（5）10分钟

29.（1）设能买A种笔记本x本，则能买B种笔记本(30-x)本．依题意得：12x+8(30-x)=300，解得x=15．因此，能购买A、B两种笔记本各15本．

（2）①依题意得：w=12n+8(30-n)，

即w=4n+240．且有  解得≤n＜12．

所以，w（元）关于n（本）的函数关系式为：w=4n+240，自变量n的取值范围是≤n＜12，且n为整数．

①对于一次函数w=4n+240，∵w随n的增大而增大，故当n为8时，w值最小．此时，30-n=22，w=4×8+240=272（元）．

因此，当买A种笔记本8本，B种笔记本22本时，所花费用最少，为272元