人教A版 (2019)必修 第一册5.4 三角函数的图象与性质导学案

这是一份人教A版 (2019)必修 第一册5.4 三角函数的图象与性质导学案，共7页。

知识点 正弦函数、余弦函数的图象
[研读]“五点法”作图中的“五点”是指函数图象的最高点、最低点以及图象与坐标轴的交点．这是作正弦函数、余弦函数图象最常用的方法．
eq \a\vs4\al(【思辨】) 判断正误(请在括号中打“√”或“×”).
(1)函数y＝sin x的图象与y轴只有一个交点．( √ )
(2)正弦曲线和余弦曲线有无数个交点．( √ )
(3)将余弦曲线向右平移 eq \f(π,2) 个单位长度就得到正弦曲线.( √ )
(4)当x∈R时，函数y＝sin x的图象与函数y＝cs x 的图象的形状完全一致．( √ )
【解析】 根据正弦函数和余弦函数的图象可知，以上说法都正确．
eq \(\s\up7(),\s\d5( “五点法”作图))
eq \a\vs4\al(例1) 用“五点法”作出函数y＝sin x＋2，x∈[0，2π]的简图．
解：列表：
在坐标系中描出五点：(0，2)， eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，3)) ，(π，2)， eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，1)) ，(2π，2)，
用光滑的曲线连接五点，得到y＝sin x＋2，x∈[0，2π]的图象，如图所示．
活学活用
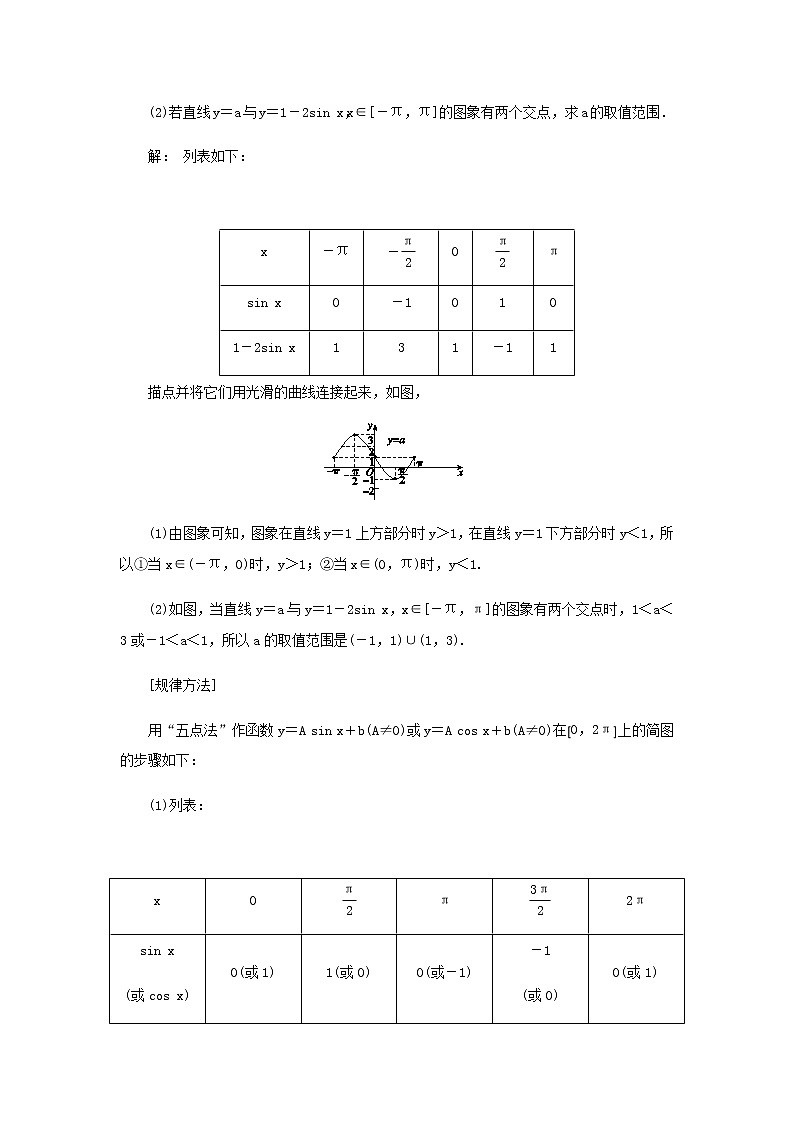
用“五点法”作出函数y＝1－2sin x，x∈[－π，π]的简图，并回答下列问题：
(1)观察函数图象，写出满足下列条件的x的区间：①y＞1；②y＜1.
(2)若直线y＝a与y＝1－2sin x，x∈[－π，π]的图象有两个交点，求a的取值范围．
解： 列表如下：
描点并将它们用光滑的曲线连接起来，如图，
(1)由图象可知，图象在直线y＝1上方部分时y＞1，在直线y＝1下方部分时y＜1，所以①当x∈(－π，0)时，y＞1；②当x∈(0，π)时，y＜1.
(2)如图，当直线y＝a与y＝1－2sin x，x∈[－π，π]的图象有两个交点时，1＜a＜3或－1＜a＜1，所以a的取值范围是(－1，1)∪(1，3).
[规律方法]
用“五点法”作函数y＝A sin x＋b(A≠0)或y＝A cs x＋b(A≠0)在 eq \b\lc\[\rc\](\a\vs4\al\c1(0，2π)) 上的简图的步骤如下：
(1)列表：
(2)描点：在平面直角坐标系中描出下列五个点：(0，y1)， eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，y2)) ，(π，y3)， eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，y4)) ，(2π，y5)，这里的yi(i＝1，2，3，4，5)值是通过函数解析式计算得到的．
(3)连线：用光滑的曲线将描出的五个点连接起来，不要用线段进行连接．
eq \(\s\up7(),\s\d5( 正弦、余弦函数图象的应用))
eq \a\vs4\al(例2) 利用正弦函数的图象，求满足sin x≥ eq \f(1,2) 的x的集合．
解：作出正弦函数y＝sin x，x∈ eq \b\lc\[\rc\](\a\vs4\al\c1(0，2π)) 的图象，如图所示，由图象可以得到在[0，2π]上满足条件的x的集合为 eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(5π,6))) ，所以满足条件的x的集合为 eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)＋2kπ，\f(5π,6)＋2kπ)) ，k∈Z．
活学活用
在(0，2π)内使sin x＞|cs x|成立的x的取值范围是( A )

A． eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)，\f(3π,4))) B． eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)，\f(π,2))) ∪ eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,4)，\f(3π,2)))
C． eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)，\f(π,2))) D． eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(5π,4)，\f(7π,4)))
【解析】 ∵sin x＞|cs x|≥0，∴sin x＞0，∴x∈(0，π).在同一坐标系中画出y＝sin x，x∈(0，π)与y＝|cs x|，x∈(0，π)的图象，如图．
观察图象易得使sin x＞|cs x|成立的x∈ eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)，\f(3π,4))) ，故选A.
eq \a\vs4\al(例3) 函数y＝lg2(2sin x＋1)的定义域为__ eq \b\lc\{(\a\vs4\al\c1(x\b\lc\|\rc\}(\a\vs4\al\c1(－\f(π,6)＋2kπ【解析】 要使函数有意义，则必有2sin x＋1>0，即sin x>－ eq \f(1,2) .结合正弦曲线，如图所示，可知函数y＝lg2(2sin x＋1)的定义域为 eq \b\lc\{(\a\vs4\al\c1(x\b\lc\|\rc\}(\a\vs4\al\c1(－\f(π,6)＋2kπ 活学活用
函数f(x)＝ eq \r(sin x) ＋ eq \f(1,\r(16－x2)) 的定义域为__(－4，－π]∪[0，π]__．
【解析】 要使函数f(x)有意义，则必有 eq \b\lc\{(\a\vs4\al\c1(sin x≥0，,16－x2>0，)) 由sin x≥0，得2kπ≤x≤2kπ＋π，k∈Z．
由16－x2>0得－4[规律方法]
用三角函数图象解三角不等式的步骤：
(1)作出相应的正弦函数或余弦函数在[0，2π]上的图象；
(2)写出适合不等式在区间[0，2π]上的解集；
(3)根据公式写出定义域内的解集．
1．对于正弦函数y＝sin x的图象，下列说法错误的是( D )
A．向左右无限伸展
B．与y＝cs x的图象形状相同，但位置不同
C．与x轴有无数个交点
D．关于y轴对称
【解析】 根据正弦函数y＝sin x的图象知，正弦函数y＝sin x的图象关于原点对称，不关于y轴对称．
2．函数y＝|sin x|的图象( D )
A．关于x轴对称 B．关于原点对称
C．关于坐标轴对称 D．关于y轴对称
【解析】 函数y＝|sin x|是偶函数，图象关于y轴对称．
3．函数y＝cs x·|tan x| eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,2) A. B.
C. D.
【解析】 y＝cs x·|tan x|
＝ eq \b\lc\{(\a\vs4\al\c1(sin x，x∈\b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2)))，,－sin x，x∈\b\lc\(\rc\](\a\vs4\al\c1(－\f(π,2)，0))，)) 故选C.
4．请补充完整下面用“五点法”作出y＝－sin x(0≤x≤2π)的图象时的列表．
①__π__；②__0__；③__1__．
【解析】 五个关键点是图象与x轴的三个交点以及图象的最高点和最低点．所以应填π，0，1.
5．若函数f(x)＝sin x＋2|sin x|，x∈[0，2π]的图象与直线y＝k有且仅有两个不同的交点，则k的取值范围是__(1，3)__．
【解析】 f(x)＝sin x＋2|sin x|
＝ eq \b\lc\{(\a\vs4\al\c1(3sin x，x∈[0，π]，,－sin x，x∈（π，2π].))
图象如图所示．
若使f(x)的图象与直线y＝k有且仅有两个不同的交点，根据图象可得k的取值范围是(1，3).
eq \a\vs4\al(温馨说明：课后请完成高效作业39 ) 函数
y＝sin x(x∈R)
y＝cs x(x∈R)
图象
图象
画法
五点法
五点法
五个
关键
点
__(0，0)__， eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，1)) ，
__(π，0)__， eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，－1)) ，
__(2π，0)__
(0，1)，__ eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，0)) __，
(π，－1)，__ eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，0)) __，
(2π，1)
x
0
eq \f(π,2)
π
eq \f(3π,2)
2π
sin x
0
1
0
－1
0
sin x＋2
2
3
2
1
2
x
－π
－ eq \f(π,2)
0
eq \f(π,2)
π
sin x
0
－1
0
1
0
1－2sin x
1
3
1
－1
1
x
0
eq \f(π,2)
π
eq \f(3π,2)
2π
sin x
(或cs x)
0(或1)
1(或0)
0(或－1)
－1
(或0)
0(或1)
y
b
(或A＋b)
A＋b
(或b)
b
(或－A＋b)
－A＋b
(或b)
b
(或A＋b)
x
0
eq \f(π,2)
①
eq \f(3π,2)
2π
－sin x
②
－1
0
③
0