人教A版 (2019)必修 第一册第五章 三角函数5.4 三角函数的图象与性质背景图课件ppt

这是一份人教A版 (2019)必修 第一册第五章 三角函数5.4 三角函数的图象与性质背景图课件ppt，共29页。PPT课件主要包含了一教材梳理填空，2π0，答案－1等内容，欢迎下载使用。

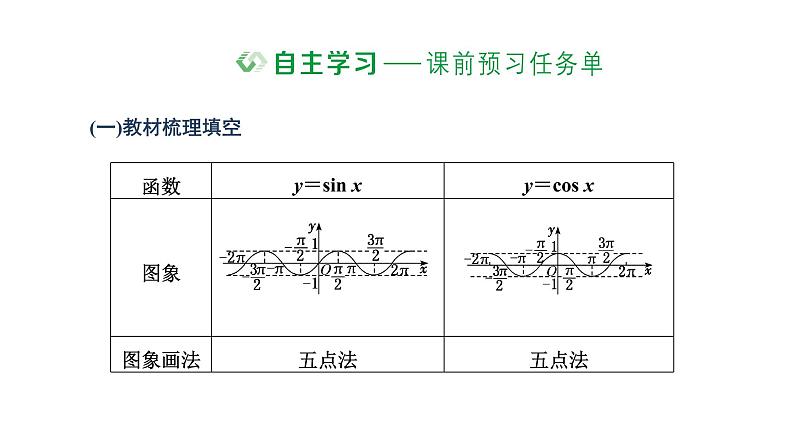
[微思考]　余弦曲线与正弦曲线完全一样吗？能否通过平移余弦曲线得到正弦曲线？
(二)基本知能小试1．判断正误(1)余弦函数y＝cs x的图象在x∈[2kπ，2kπ＋2π](k∈Z)上的图象形状相同，只是位置不同．(　　)(2)正弦函数y＝sin x(x∈R)的图象关于x轴对称．(　　)(3)余弦函数y＝cs x(x∈R)的图象关于原点成中心对称．(　　)答案：(1)√　(2)×　(3)×
解析：观察y＝cs x，x∈R的图象可知，直线x＝0即y轴是一条对称轴．答案：B　3．函数y＝sin x，x∈[0，π]的图象与直线y＝0.8的交点有 (　　)A．1个 B．2个C．3个 D．4个解析：观察图象(略)易知：有两个交点．答案：B
题型一　用“五点法”画正弦、余弦函数的简图　 【学透用活】画正弦函数、余弦函数的图象应注意的问题(1)无论采用什么方法作正弦、余弦函数的图象，函数自变量都要用弧度制，这样自变量的值为实数，任意角与x轴上的实数产生了一一对应关系，从而可以在平面直角坐标系中作出图象．(2)正弦、余弦曲线形状相同，位置不同，均向左、向右无限延伸，与x轴有无数个交点，正弦曲线关于原点对称，而余弦曲线关于y轴对称．(3)画图时要注意图象的对称性和凹凸方向．切忌把图象画成折线．
[典例1]　用“五点法”作出下列函数的简图：(1)y＝sin x－1，x∈[0,2π]；(2)y＝2＋cs x，x∈[0,2π]．[解]　(1)列表：描点连线，如图所示．
(2)列表：描点连线，如图所示．
[方法技巧]用“五点法”画函数y＝Asin x＋b(A≠0)或y＝Acs x＋b(A≠0)在[0,2π]上简图的步骤(1)列表：
【对点练清】用“五点法”画出y＝sin x＋2，x∈[0,2π]的简图．解：(1)列表：
题型二　正弦(余弦)函数图象的应用　 [探究发现](1)方程sin x＝x的实根个数有多少个？提示：在同一坐标系内分别作出y＝sin x，y＝x的图象(略)，可知当x∈(－∞，0)时，sin x＞x；当x∈(0，＋∞)时，sin x＜x，当x＝0时，sin x＝x，所以方程只有一个实根为0.(2)函数f(x)＝ －cs x在[0，＋∞)内有多少个零点？提示：令f(x)＝0，所以 ＝cs x，分别作出y＝ ，y＝cs x的图象(略)，可知两函数只有一个交点，所以f(x)在[0，＋∞)内只有一个零点.
[方法技巧]解决三角函数图象应用问题的策略(1)用三角函数的图象解sin x＞a(或cs x＞a)的方法：①作出y＝a，y＝sin x(或y＝cs x)的图象．②确定sin x＝a(或cs x＝a)的x值．③确定sin x＞a(或cs x＞a)的解集．(2)判断方程解的个数，或由方程解的个数确定参数的取值范围，可利用图象解题，当方程含有正、余弦函数时，可借助正、余弦曲线探究问题的解法．　　
【对点练清】1．[变条件]本例(1)中的“sin x”改为“cs x”，应如何解答？
二、创新性——强调创新意识和创新思维2．结合函数f(x)＝sin|x|＋|sin x|的图象，你能得到哪些结论？(答案不唯一)解：作出函数f(x)的图象如图中粗实线所示．由图象可以得到：①奇偶性：f(－x)＝sin|－x|＋|sin(－x)|＝sin|x|＋|sin x|＝f(x)，则函数f(x)是偶函数．②图象的对称性：函数图象关于y轴对称．
⑤函数的值域为[0,2]．⑥f(x)在[－π，π]有3个零点．当0≤x≤π时，f(x)＝sin|x|＋|sin x|＝sin x＋sin x＝2sin x，由f(x)＝0得2sin x＝0得x＝0或x＝π，由f(x)是偶函数，得在[－π，π)上还有一个零点x＝－π，即函数f(x)在[－π，π]有3个零点．⑦若g(x)＝a，则f(x)－g(x)＝0有根的条件为0≤a≤2等等．(任选几个写出即可)
“课时跟踪检测”见“课时跟踪检测（三十八）” (单击进入电子文档)