2021学年1 探索勾股定理习题课件ppt

这是一份2021学年1 探索勾股定理习题课件ppt，共28页。PPT课件主要包含了答案显示，相等60°，见习题，斜边的一半等内容，欢迎下载使用。

1．三个角都________的三角形是等边三角形；有一个角等于________的等腰三角形是等边三角形．
2．如图，等边三角形ABC的边长为2，CD平分∠ACB，交AB于点D，DE∥BC，则△ADE的周长为(　　)A．2B．2.5C．3D．4
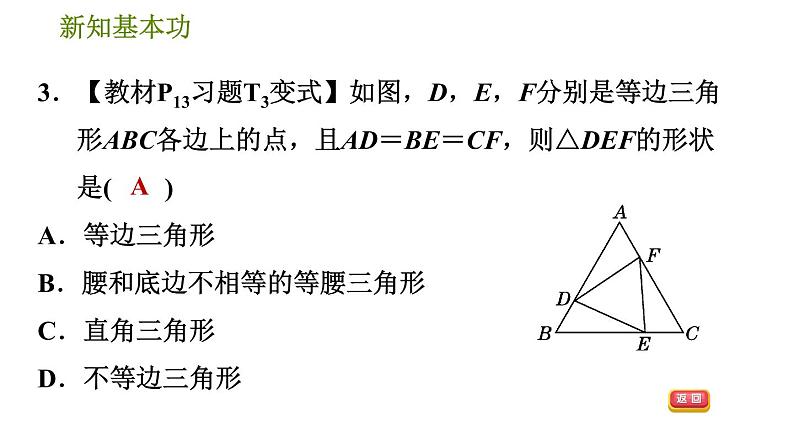
3．【教材P13习题T3变式】如图，D，E，F分别是等边三角形ABC各边上的点，且AD＝BE＝CF，则△DEF的形状是(　　)A．等边三角形B．腰和底边不相等的等腰三角形C．直角三角形D．不等边三角形
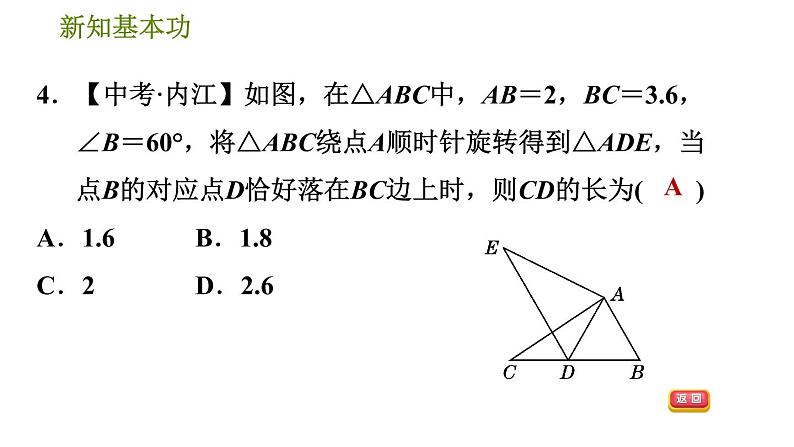
4．【中考·内江】如图，在△ABC中，AB＝2，BC＝3.6，∠B＝60°，将△ABC绕点A顺时针旋转得到△ADE，当点B的对应点D恰好落在BC边上时，则CD的长为(　　)A．1.6B．1.8C．2D．2.6
5．在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于______________．
6．【2021·福建】如图，某研究性学习小组为测量学校A与河对岸工厂B之间的距离，在学校附近选一点C，利用测量仪器测得∠A＝60°，∠C＝90°，AC＝2 km.据此，可求得学校与工厂之间的距离AB等于(　　)A．2 km 　　　B．3 kmC．2 km 　　　D．4 km
7．如图，在△ABC中，AB＝AC，∠B＝30°，AD⊥AB，AD交BC于点D，AD＝4，则BC的长为(　　)A．8 　　　B．4C．12 　　　D．6
8．如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，EF交BC的延长线于点F.若CD＝2，则DF的长为(　　)A．1 　　　B．2C．3 　　　D．4
9．如图，在△ABC中，AB＝AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E，F.(1)求证：DE＝DF；
(2)若∠A＝60°，BE＝1，求△ABC的周长．
10．如图，在△ABC中，AB＝AC，∠BAC＝120°，AE＝BE，D为EC的中点．(1)求∠CAE的度数；
(2)求证：△ADE是等边三角形．
11．【2020·烟台】如图，在等边三角形ABC中，点E是AC上一定点，点D是直线BC上一动点，以DE为一边作等边三角形DEF，连接CF.【问题解决】如图①，若点D在BC上，求证：CE＋CF＝CD.
证明：在CD上截取CH＝CE，连接EH，如图①所示．∵△ABC是等边三角形，∴∠ECH＝60°.∴△CEH是等边三角形．∴EH＝EC＝CH，∠CEH＝60°.∵△DEF是等边三角形，∴DE＝FE，∠DEF＝60°.∴∠DEH＋∠HEF＝∠FEC＋∠HEF＝60°.∴∠DEH＝∠FEC.
【类比探究】如图②，若点D在BC的延长线上，请探究线段CE，CF与CD之间存在怎样的数量关系？并说明理由．
解：线段CE，CF与CD之间的等量关系是CF＝CD＋CE.理由如下：∵△ABC是等边三角形，∴∠A＝∠B＝60°.过D作DG∥AB，交AC的延长线于点G，如图②所示．∵GD∥AB，∴∠GDC＝∠B＝60°，∠DGC＝∠A＝60°，∴∠GDC＝∠DGC＝∠DCG＝60°.∴△GCD为等边三角形． ∴DG＝CD＝CG.
12．如图，等边三角形ABC的边长为8，D为AB边上一动点，过点D作DE⊥BC于点E，过点E作EF⊥AC于点F.(1)若AD＝2，求AF的长；
(2)当AD取何值时，DE＝EF?
13．如图，已知△ABC为等边三角形，延长BC到点D，延长BA到点E，并且使AE＝BD，连接CE，DE.求证：EC＝ED.