湘教版（2019）必修 第一册4.3 对数函数课文课件ppt

这是一份湘教版（2019）必修 第一册4.3 对数函数课文课件ppt，共23页。PPT课件主要包含了内容索引，课前篇自主预习，课堂篇探究学习，情境导入，知识梳理，正数才有对数，答案C，答案B等内容，欢迎下载使用。

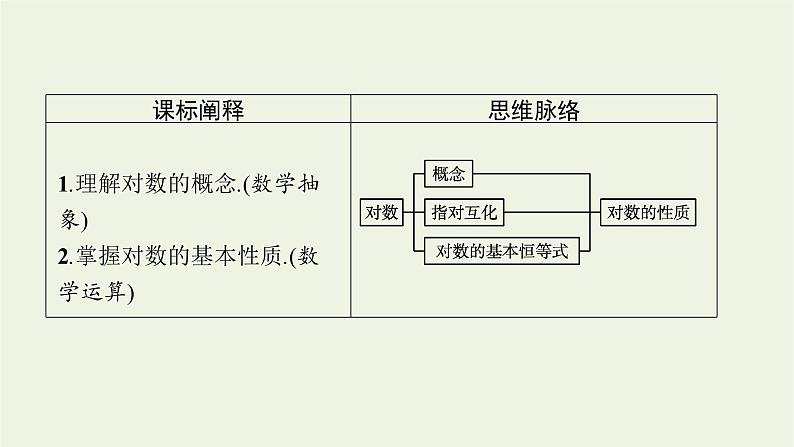
1.理解对数的概念.(数学抽象)2.掌握对数的基本性质.(数学运算)
心理学上有一个著名的“荷花定律”,它讲述的是这样的一种现象:池塘里种满了荷花,荷花第一天开一朵,第二天开两朵,第三天开四朵,第四天开八朵……以此类推,每天荷花开放的数量都是前一天的两倍,第30天的时候刚好开满整个池塘,那么在第几天的时候荷花刚好开满半个池塘呢?是第15天吗?不对,应该是最近尾声的第29天.下面我们从数学的角度理解这个问题.设第x天荷花开了2x朵,那么第几天荷花开了16朵,64朵,63朵呢?对于2x=63,这个方程我们会解吗?如何求x?这种求x值的方法就是我们要学习的“对数”.
知识点:对数的概念1.对数的定义:如果ab=N(a>0且a≠1),那么b叫作以a为底,(正)数N的对数,记作 b=lgaN ,这里,a叫作对数的底数,N叫作对数的真数.
2.对数的基本恒等式:
名师点析 1.“lg”同+、-、×等符号一样,表示一种运算,即已知一个底数和它的幂求指数的运算,这种运算叫对数运算,不过对数运算的符号写在数的前面.另外“lg”和“ ”有些类似,都是为了引入一类实数而创造的符号.2.对数恒等式 =N(N>0,a>0,且a≠1)的特点:指数中含有对数形式;同底,即幂底数和对数的底数相同;其值为对数的真数.
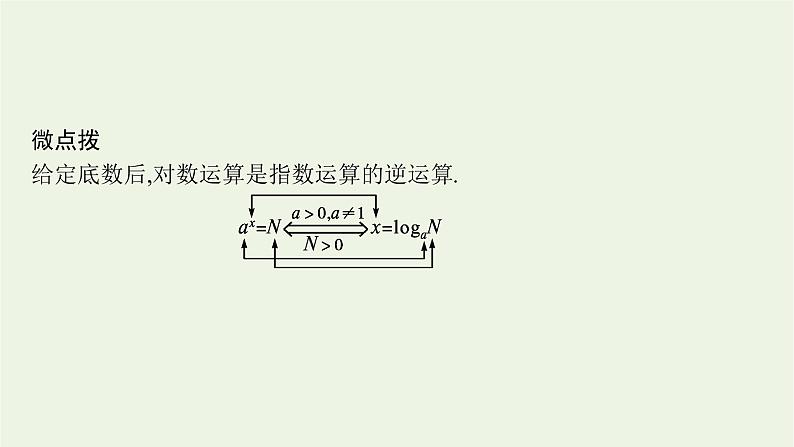
微点拨给定底数后,对数运算是指数运算的逆运算.
微练习(1)lgaa=　　　　　,用文字语言可以叙述为　　　　　; (2)lga1=　　　　　,用文字语言可以叙述为　　　　　. (3)若lg3(lg2x)=0,则x=　　　　　. 
答案 (1)1　底的对数为1(2)0　1的对数为0(3)2解析 (3)由已知得lg2x=1,故x=2.
例1将下列指数式与对数式互化:
分析利用当a>0,且a≠1时,lgaN=b⇔ab=N进行互化.
要点笔记将指数式化为对数式,只需将幂作为真数,指数作为对数,底数不变;而将对数式化为指数式,只需将对数式的真数作为幂,对数作为指数,底数不变.
变式训练1将下列指数式与对数式互化:
例2求下列各式中x的值:(1)4x=5·3x;(2)lg7(x+2)=2;
要点笔记求对数式lgaN=m(a>0,且a≠1,N>0)中的有关量的方法:将lgaN=m写成指数式am=N后,将N写成以a为底的指数幂N=ab,则m=b,即lgaN=b.
变式训练2求下列各式中的x值:
例3求下列各式中x的值:(1)lg2(lg2x)=0;
解 (1)∵lg2(lg2x)=0,∴lg2x=1,∴x=21=2.
反思感悟 1.利用对数性质求解两类问题的解法(1)求多重对数式的值的解题方法是由内到外,逐步脱去“lg”后再求解,如求lga(lgbc)(a>0,且a≠1,b>0,b≠1,c>0)的值,先求lgbc的值,再求lga(lgbc)的值.(2)注意结论的应用:若lgaf(x)=0,则f(x)=1;若lgaf(x)=1,则f(x)=a,其中a>0且a≠1,f(x)>0.2.对指数中含有对数值的式子进行化简、求值时,应充分考虑对数的基本恒等式的应用.
变式训练3求下列各式中x的值:(1)lg2(lg5x)=0;
代入法解决条件求值问题
1.对数式lg(a-2)(5-a)中实数a的取值范围是(　　)A.(-∞,5)B.(2,5)C.(2,3)∪(3,5)D.(2,+∞)