






2020-2021学年6.2 一次函数背景图ppt课件
展开(1)下列哪个函数为一次函数( )
A:y=x2+2 B:y-3x=2x+1C:y= -3 D:y2=2x-3
(2)下列说法中,正确的是( ) A、一次函数是正比例函数 B、正比例函数是一次函数 C、正比例函数不是一次函数 D、一次函数不可能是正比例函数
(1)已知函数y=4x+5, 当x=-3时,y=____; 当y=5时,x=____.
(2)已知函数y=-3x+1, 当x=2时,y=____; 当y=0时,x=____.
6.2 一次函数(2)
写出下列各题中y与 x之间的函数表达式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)摩托车以50千米/时的速度匀速行驶,行驶路程y(km)与行驶时 间x(h)之间的关系;
(3)一棵树现在高40厘米,每个月长高3厘米,x月后这棵树的高度为y(厘米);
(4)多边形的内角和s与边数n的函数关系.
一盘蚊香长105cm,点燃时每小时缩短10cm,(1)写出蚊香点燃后的长度y(cm)与蚊香燃烧时间t(h)之间的函数表达式;(2)该盘蚊香可燃烧多长时间?
甲、乙两地相距520km,一辆汽车以80km/h的速度从甲地开往乙地,行驶了t(h).试问剩余路程s(km)与行驶时间t(h)之间有怎样的函数解析式?并求t的取值范围.
解:s=520-80t (0≤t ≤6.5).
1、已知正比例函数y=kx,当x=3时,y=2,求函数的表达式。
2、已知一次函数y=kx+b,当x=-3时,y=0;当x=0时,y=-4;求函数的表达式。
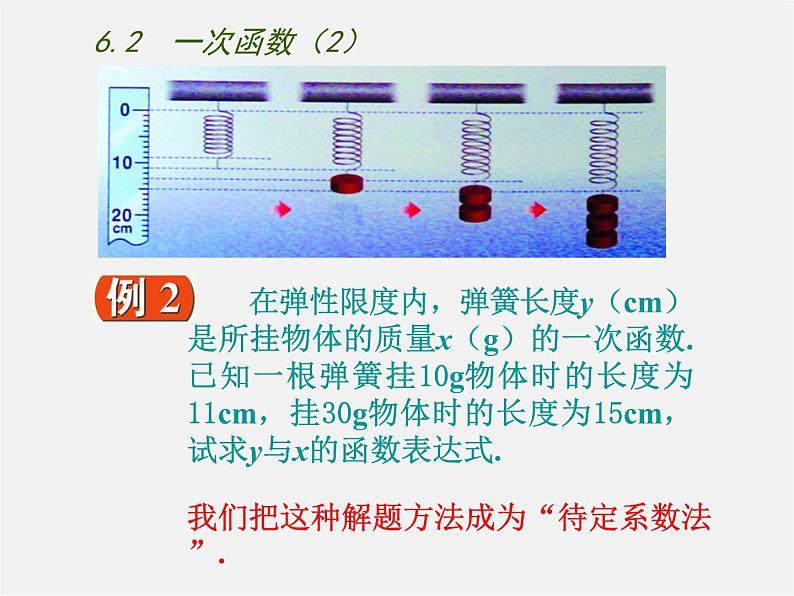
在弹性限度内,弹簧长度y(cm)是所挂物体的质量x(g)的一次函数.已知一根弹簧挂10g物体时的长度为11cm,挂30g物体时的长度为15cm,试求y与x的函数表达式.
我们把这种解题方法成为“待定系数法”.
如何用“待定系数法”确定一次函数的表达式?
用待定系数法确定一次函数表达式的一般步骤是:①设一次函数的表达式y=kx+b(k≠0);②把已知条件代入表达式得到关于k、b的方程 (组);③解方程(组),求出k、b的值;④将k、b的值代回所设的表达式. 一次函数的表达式中有两个待定系数,因而需要两个条件.
某产品每件的销售价x元与产品的日销售量y件之间的关系如下表:若日销售量y是销售价x的一次函数.(1)求出日销售量y件与销售价x元的函数表达式;
(2)若该产品每件成本10元,销售价定为30元时,求每日的销售利润.
解: (1)设此函数表达式为y=kx+b,则由题意得, 15k+b=25 , 解之得 k=-1, 20k+b=20 , b=40.所以函数表达式为:y=-x+40.
(2)当x=30时,y=-30+40=10(件),(30-10)×10=200(元).答:每日的销售利润为200元.
已知y与x成正比例,且当x=1时, y=6. (1)求y与x之间的函数关系式; (2)y=2时,求x的值。
变式: 已知:y与x-1成正比例,且当x=-5时,y=3,求y与x之间的函数关系式。
变式: 已知:y-2与x成正比例,且当x=-5时,y=3,求y与x之间的函数关系式。
变式: 已知:y-2与x-1成正比例,且当x=-5时,y=3,求y与x之间的函数关系式。
已知y与z成正比例,z+1与x成正比例,且当x=1时,y=1当x=0时, y=-3,求y与x的函数关系。
小结: ①题中两个成正比例,系数不一定相同,必须用两个不同的字母来表示,不能误写成同一个k. ②解题中k1、k2可当作一个整体.
练习:已知y=y1+y2,其中y1与x成正比例,y2与(x-2)成正比例,又当x=-1时,y=2;当x=2时,y=5.求y与x的函数关系式。
通过这节课的学习对自己说,你有哪些收获?对同学说,你有哪些温馨提示?对老师说,你有哪些困惑?
(确定一次函数的解析表达式)
这两节课我们主要研究了一次函数的表达式,一次函数的图像又具有什么特点呢?请以一具体实例画图说明.
苏科版八年级上册6.2 一次函数图文课件ppt: 这是一份苏科版八年级上册6.2 一次函数图文课件ppt,共11页。PPT课件主要包含了展望中考等内容,欢迎下载使用。
苏科版八年级上册6.2 一次函数课文ppt课件: 这是一份苏科版八年级上册6.2 一次函数课文ppt课件,共16页。PPT课件主要包含了y15+01x,y120+30x,2y=3x2+2,3m=-5n,62y=x-1,典型例题,牛刀小试等内容,欢迎下载使用。
初中数学苏科版八年级上册6.2 一次函数教学课件ppt: 这是一份初中数学苏科版八年级上册6.2 一次函数教学课件ppt,共15页。PPT课件主要包含了1完成下表,y15+01x,y120+30x,一次函数,正比例函数,2y=3x2+2,3m=-5n,62y=x-1,7y=,不是一次函数等内容,欢迎下载使用。














