人教版八年级上册11.3.2 多边形的内角和背景图ppt课件

这是一份人教版八年级上册11.3.2 多边形的内角和背景图ppt课件，共24页。PPT课件主要包含了学习目标，知识回顾，探索与思考，n-2，n-3，完成下表，巩固练习，x65°，x95°，填空题等内容，欢迎下载使用。

(1)掌握多边形的内角和的计算方法，并能用内角和知识解决一些较简单的问题；(2)通过多边形内角和的计算公式的推导，培养探索和归纳的能力；(3) 体验转化的数学思想方法。
重点与难点：(1)重点:多边形内角和以及外角和；(2)难点:多边形内角和以及外角和的推导。
３、三角形的内角和是_____度．
２、在多边形中连接______________________的线段叫做多边形的对角线。
1、在平面内，___________________________叫做多边形。
由一些线段首尾顺次相接组成的图形
多边形不相邻的两个顶点
4、正方形的内角和是 度，长方形的内角和是 度。
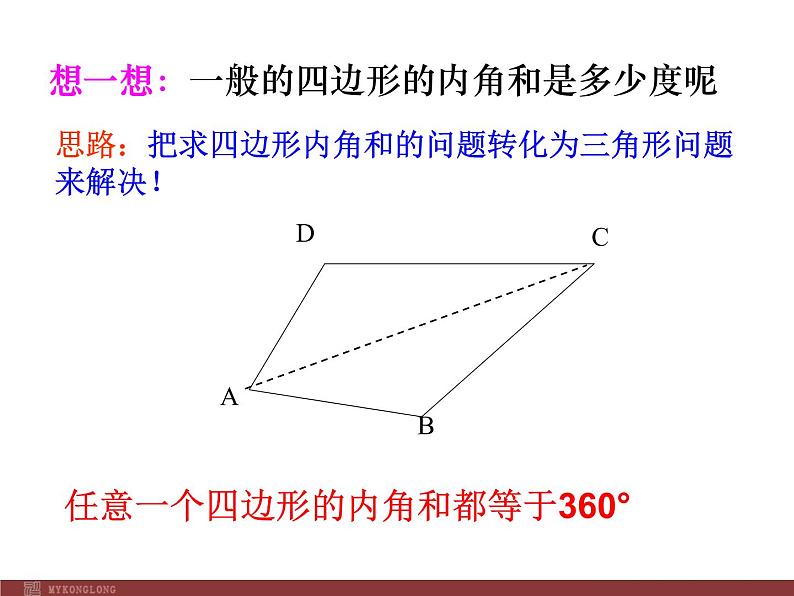
任意一个四边形的内角和都等于360°
思路：把求四边形内角和的问题转化为三角形问题来解决！
想一想：一般的四边形的内角和是多少度呢
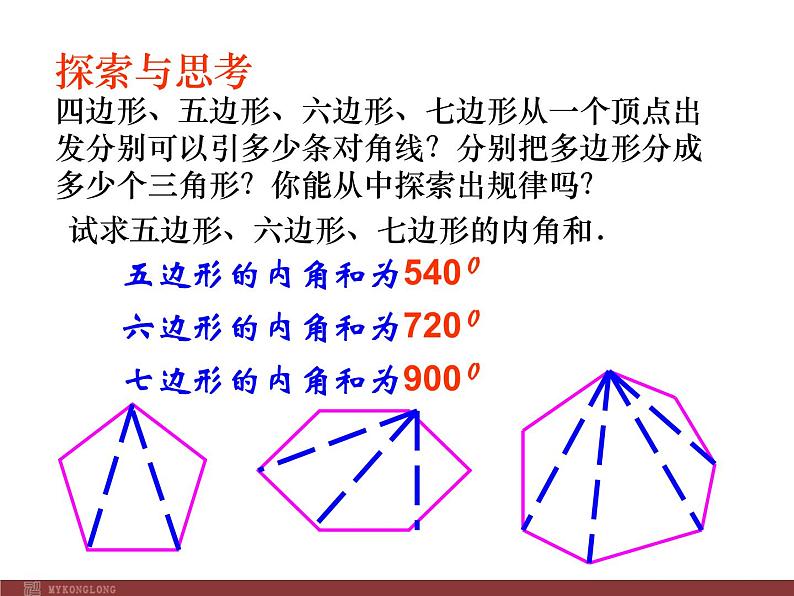
五边形的内角和为540０
七边形的内角和为900０
六边形的内角和为720０
四边形、五边形、六边形、七边形从一个顶点出发分别可以引多少条对角线？分别把多边形分成多少个三角形？你能从中探索出规律吗？
试求五边形、六边形、七边形的内角和．
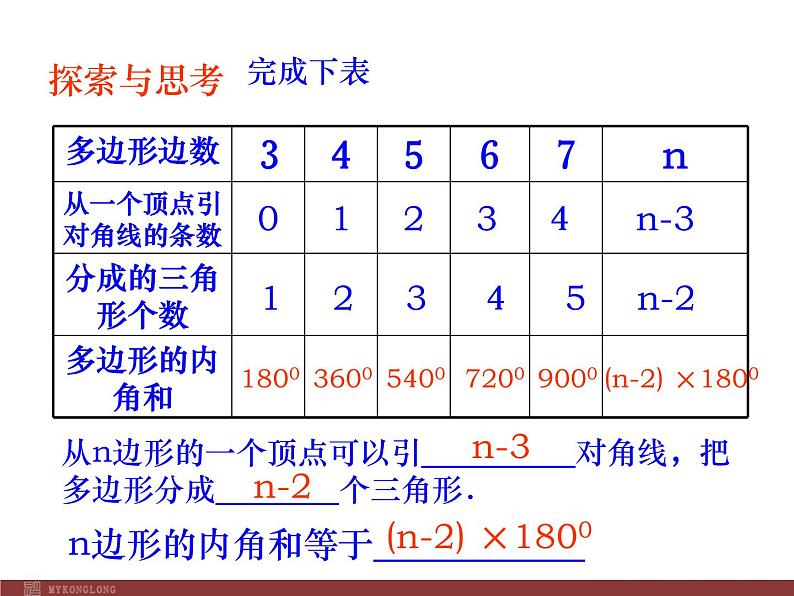
(n-2) ×1800
从n边形的一个顶点可以引＿＿＿＿＿对角线，把多边形分成＿＿＿＿个三角形．
n边形的内角和等于＿＿＿＿＿＿
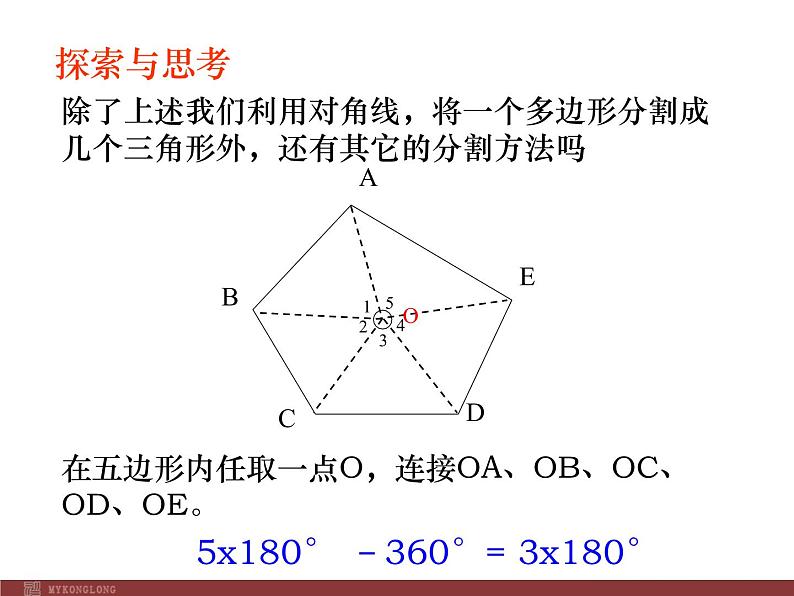
5x180° –360°= 3x180°
在五边形内任取一点O，连接OA、OB、OC、OD、OE。
除了上述我们利用对角线，将一个多边形分割成几个三角形外，还有其它的分割方法吗
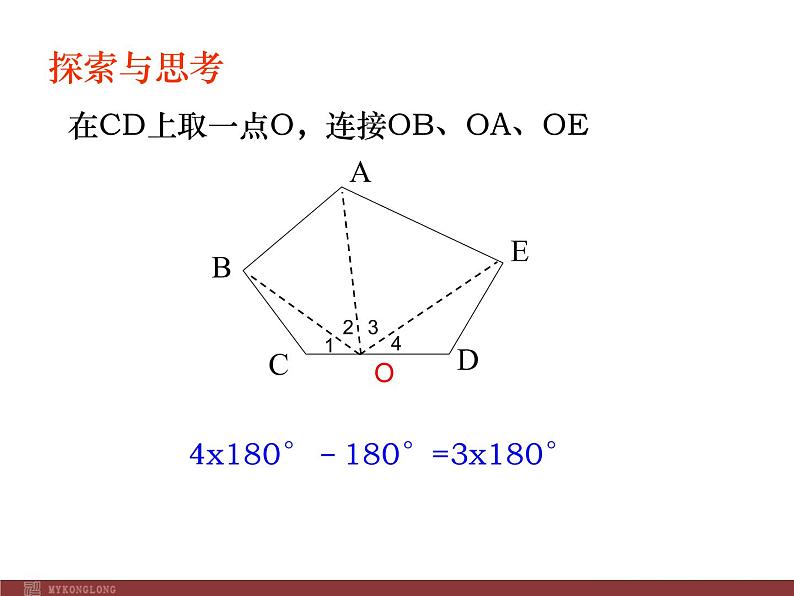
4x180°–180°=3x180°
在CD上取一点O，连接OB、OA、OE
1. 求下列图形中 x 的值 .
2x+140+90=360
360-80-120-75=180-x
（2）七边形的内角和等于______度.
（3）一个多边形的内角和等于720 °,那么这个多边形是______边形.
（4）如果一个四边形的一组对角互补，那么另一组对角__________
（1）多边形的内角和随着边数的增加而______，边数增加一条时，它的内角和增加________度 .
如图，在六边形的每一个顶点处各取一个外角，这些外角的和叫做六边形的外角和. 六边形的外角和等于多少度？
解：如图，六边形ABCDEF中， ∠1+∠7=180 °，∠2+∠8=180 °， ∠3+∠9=180 °，∠4+∠10=180 °， ∠5+∠11=180 °，∠6+∠12=180 °.
∵ ∠7+∠ 8+∠9+ ∠10 +∠11+ ∠12 =（6－2）×180 °= 720°,
多边形的外角和等于360°.
∴ ∠1+∠ 2+∠3+ ∠4 +∠5+ ∠6 = 6×180 °－720 ° = 360°.
对于 n 边形，结论仍然成立！
多边形的外角和等于＿＿＿＿＿＿
1、n边形的内角和等于______________，九边形的内角和等于_______________________。
2、一个多边形的内角和等于1440°，那么它是______边形，它的外角和为＿＿＿＿。
3、正五边形的每一个内角的度数是_______，每个外角度数为＿＿＿＿。
4、从六边形的一个顶点出发可画_____条对角线，这些对角线把六边形分成_____个三角形。
5、一个六边形共有_____条对角线。
(n - 2) • 180°
(9 - 2) • 180°
2、四边形ABCD的内角∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4，求各个角的大小。
则∠B=2x°,∠C=3x°,∠D=4x°
因为∠A+ ∠B+∠C+∠D=360°
所以x+2x+3x+4x=360
∠A=36°, ∠B=72°,∠C=108°,∠D=144°
3、过某个多边形一个顶点的所有对角线，将这个多边形分成5个三角形。这个多边形是几边形？它的内角和是多少？
设这个多边形的边数为n，
内角和=(n-2)x180°
=(5-2)x180°
答：这个多边形是七边形，它的内角和是900°
4、一个多边形的内角和等于外角和的 ，求这个多边形的边数。
答：这个多边形的边数为11。
1、在四边形的四个内角中，最多有_____个钝角,最多能有______个锐角. 2、一个多边形的每个内角都是150°,它是____边形。3、已知一个多边形，它的内角和等于五边形的内角和的2倍，这个多边形是_______边形．4、已知一个多边形的边数恰好是从一个顶点所画的对角线的条数的2倍,则此多边形是______边形.5、一个多边形的边数增加1，则内角和增加的度数是(     )A.60°        B.90°       C.180°       D.360°
6、如图:某居民小区搞绿化,分别在三角形、四边形、五边形的广场各角修建半径为1米的花坛.小区绿化组长想先求花坛的面积,再根据面积买花苗.你能帮绿化组长求出花坛的面积吗?（结果保留π）
解:假设这个多边形的边数是n，那个内角的度数为x
则有：(n-2)x180=2750+x
因为n是正整数,所以2750+x也是180的倍数
所以(n-2).180=2880
1、已知一个多边形除了一个内角外，其余各内角的和是2750°，求这个多边形的边数。
解：因为五边形是正五边形
所以∠BAE=∠DAE
所以∠FAE=72°，∠FEA=72°
2、 如图：我国的国旗上的五星是正五角星，正五角星中的五边形ABCDE是正五边形，你能求出五角星中∠F的度数？
3、把一个五边形锯去一个内角后得到是什么图形？此时，多边形的内角和与外角和有什么变化？
解：五边形锯去一个内角后得到的图形可能是四边形，如图①；五边形，如图②；六边形，如图③
其内角和分别是360°，540°，720°。
是原来的多边形内角和度数本身,少180度和多180度
1、n（n≥3）边形的的内角和为（n-2)x180°
2、任意多边形的外角和等于360°
4、多边形的边数与内角和及外角和的关系：
内角和与边数成正比，边数增加，内角和增加，边数减少，内角和减少，每增加一条边，内角和增加180°（反过来也成立），边数的内角和是180°的整数倍。多边形的外角和恒等于360°，与边数多少无关。
5、正n(n≥3）边形的的内角和为