




初中数学冀教版七年级下册7.4 平行线的判定授课课件ppt
展开利用“内错角相等”说明两直线平行利用“同旁内角互补”说明两直线平行
判断两直线平行的方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行. 简单地说,同位角相等,两直线平行.
利用“内错角相等”说明两直线平行
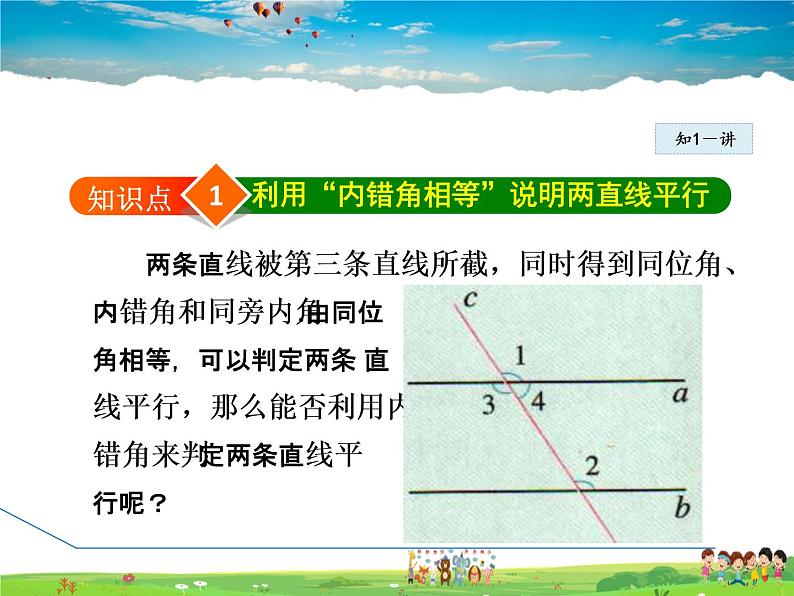
两条直线被第三条直线所截,同时得到同位角、 内错角和同旁内角.由同位角相等,可以判定两条 直线平行,那么能否利用内错角来判 定两条直线平行呢?
判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条 直线平行. 简单说成:内错角相等,两直线平行.
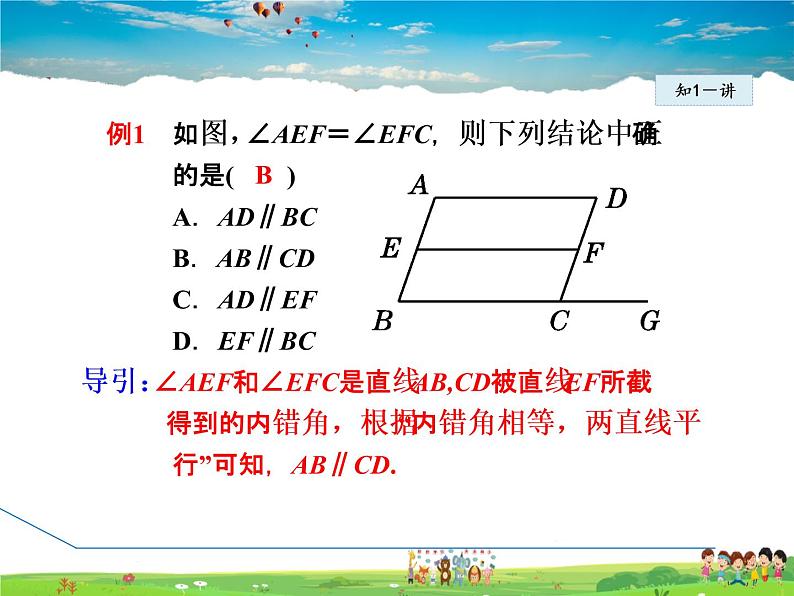
例1 如图,∠AEF=∠EFC,则下列结论中正 确 的是( ) A.AD∥BC B.AB∥CD C.AD∥EF D.EF∥BC 导引:∠AEF和∠EFC是直线AB,CD被直线EF所截 得到的内错角,根据“内错角相等,两直线平 行”可知,AB∥CD.
利用内错角相等来判定两直线平行的方法:(1)看两角是不是两直线被第三条直线截得的角;(2)看两角是不是由上述直线形成的内错角,若是, 看其是否相等.若相等,则两条直线平行.
例2 如图,已知∠ADE=60°,DF平分∠ADE, ∠1=30°,试 说明:DF∥BE. 导引:要想说明DF∥BE,可通过说明∠1=∠EDF 来实现,由于∠1=30°,所以只需求出∠EDF =30°,而这个结论可通过DF是∠ADE的平分 线来求得.
解:∵DF平分∠ADE(已知), ∴∠EDF= ∠ADE(角平分线的定义). 又∵∠ADE=60°, ∴∠EDF=30°. 又∵∠1=30°(已知), ∴∠EDF=∠1, ∴DF∥BE(内错角相等,两直线平行).
要判定两直线平行可以通过说明同位角相等或内错角相等来实现,至于到底选用同位角还是选用内错角,要看具体的题目,要尽可能与已知条件联系.
如图,已知∠1=∠2,则图中互相平行的线段是____________.
如图,已知∠1=120°,当∠2=________时,a∥b,理由是_________________________.
内错角相等,两直线平行
(中考·福州)下列图形中,由∠1=∠2能得到AB∥CD的是( )
如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )A.∠1=∠2 B.∠2=∠3C.∠3=∠4 D.∠4=∠5
如图,若∠1与∠2互补,∠2与∠4互补,则( )A.l4∥l5 B.l1∥l2 C.l1∥l3 D.l2∥l3
利用“同旁内角互补”说明两直线平行
探究 遇到一个新问题时,常常把它转化为已知的(或已解决的)问题. 这一节中,我们是怎样利用“同位角相等,两直线平行”得到“内错角相 等,两直线平行”的?你能利用“同位角相等,两直线平行”或“内错角相等,两直线平行”得到“同旁内角互补,两直线平行”吗?
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行. 表达方式:如图:∵∠1+∠2=180°(已知),∴a∥b(同旁内角互补,两直线平行).
如图,已知直线AB,CD被直线EF所截,∠1=60°,∠2=120°. 对AB∥CD说明理由.
∵∠1+∠2=60°+120°=180° (已知), ∠2=∠4 (对顶角相等),∴∠1+∠4=180° (等量代换).∴AB∥CD (同旁内角互补,两直线平行).
1.本题运用数形结合思想.平行线的判定是由角之间 的数量关系到“形”的判定.要判定两直线平行,可 围绕截线找同位角、内错角或同旁内角,若同位角 相等、内错角相等或同旁内角互补,则两直线平行.2.用同位角相等、内错角相等或同旁内角互补中的一 个方法说明两直线平行时,一般都要通过结合对顶角、 邻补角等知识来说明.
例4 如图,∠1=65°,∠2=65°,∠3=115°,试 说明(1)DE∥BC; (2)DF∥AB. 根据图形,完成下列推理: (1)∵∠1=65°,∠2=65°, ∴∠1=∠2. ∴_____∥_____( ). (2)∵AB,DE相交,∴∠1=∠4( ). ∴∠4=65°,又∵∠3=115°, ∴∠3+∠4=180°, ∴_____∥____( ).
同旁内角互补,两直线平行
同位角相等,两直线平行
∠1与∠2是直线DE,BC被直线AB所截得到的同位角,所以DE∥BC,理由是“同位角相等,两直线平行”.∠1与∠4是两条直线AB与DE相交得到的对顶角,所以∠1=∠4,理由是“对顶角相等”,∠3与∠4是直线DF,AB被直线DE所截得到的同旁内角,所以DF∥AB,理由是“同旁内角互补,两直线平行”.
(1)由两角相等或互补关系,判定两条直线平行,其 关键是找出两个角是哪两条直线被哪一条直线所 截而成的角.(2)是选用两角相等,还是选用互补关系说明两直线 平行,应根据实际图形,灵活运用其中一种方法 说明即可.
判定两直线平行的方法:方法一:平行线的定义:在同一平面内,不相交的两 条直线就是平行线.方法二:如果两条直线都和第三条直线平行,那么这 两条直线也互相平行.方法三:同位角相等,两直线平行.方法四:内错角相等,两直线平行.方法五:同旁内角互补,两直线平行.方法六:在同一平面内,垂直于同一条直线的两条直 线平行.
如图,直线a,b被直线c所截,如果同位角∠1=∠5,请你写出图中其他相等的同位角、所有相等的内错角、所有互补的同旁内角.
其他相等的同位角:∠3=∠7;∠2=∠6;∠4=∠8.相等的内错角:∠3=∠6,∠4=∠5.互补的同旁内角:∠3+∠5=180°,∠4+∠6=180°.
【2016·赤峰】如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )A.AB∥BC B.BC∥CDC.AB∥DC D.AB与CD相交
【中考·山西】如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )A.∠1=∠3 B.∠2+∠4=180°C.∠1=∠4 D.∠3=∠4
(中考·长春)如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )A.15° B.30° C.45° D.60°
如图,点E在BC的延长线上,下列条件中能判定BC∥AD的是( )A.∠1=∠2 B.∠DAB+∠D=180°C.∠3=∠4 D.∠B=∠DCE
1.由“内错角相等”判定两直线平行:内错角相等, 两直线平行.2.由“同旁内角”判定两直线平行:同旁内角互补, 两直线平行.
如图,下列推理正确的有( )①因为∠1=∠4,所以BC∥AD;②因为∠2=∠3,所以AB∥CD; ③因为∠BCD+∠ADC=180°,所以AD∥BC;④因为∠1+∠2+∠C=180°,所以BC∥AD.A.1个 B.2个 C.3个 D.4个
易错点:不能准确识别截线和被截线,从而误判两 直线平行.
在分不清截线和被截线的情况下,容易误认为①②④也是正确的.
数学七年级下册7.4 平行线的判定图文ppt课件: 这是一份数学七年级下册7.4 平行线的判定图文ppt课件,共19页。
初中数学冀教版七年级下册7.4 平行线的判定精品课件ppt: 这是一份初中数学冀教版七年级下册7.4 平行线的判定精品课件ppt,文件包含河北教育版数学七年级下·74平行线的判定教学课件pptx、74平行线的判定教案docx、74平行线的判定同步练习docx等3份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
初中冀教版7.3 平行线习题课件ppt: 这是一份初中冀教版7.3 平行线习题课件ppt,共14页。PPT课件主要包含了答案呈现,习题链接,等角的余角相等,对顶角相等等内容,欢迎下载使用。













