人教版八年级上册第十二章 全等三角形综合与测试达标测试

这是一份人教版八年级上册第十二章 全等三角形综合与测试达标测试，共14页。

1．如果两个图形全等，那么这两个图形必定是（ ）
A．形状大小均相同B．形状相同，但大小不同
C．大小相同，但形状不同D．形状大小均不相同
2．△ABC≌△DEF，下列结论中不正确的是（ ）
A．AB＝DEB．BE＝CFC．BC＝EFD．AC＝DE
3．下列判定直角三角形全等的方法，不正确的是（ ）
A．两条直角边对应相等
B．两个锐角对应相等
C．斜边和一直角边对应相等
D．斜边和一锐角对应相等
4．如图，△ABC≌△AED，点E在线段BC上，∠1＝40°，则∠AED的度数是（ ）
A．70°B．68°C．65°D．60°
5．如图，若△ABC≌△DEF，且BE＝5，CF＝2，则BF的长为（ ）
A．2B．3C．1.5D．5
6．如图，公园里有一座假山，要测假山两端A，B的距离，先在平地上取一个可直接到达A和B的点C，分别延长AC，BC到D，E，使CD＝CA，CE＝CB，连接DE．这样就可利用三角形全等，通过量出DE的长得到假山两端A，B的距离．其中说明两个三角形全等的依据是（ ）
A．SSSB．ASAC．AASD．SAS
7．如图，已知∠BAC＝∠DAC那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
A．AB＝ADB．CB＝CDC．∠BCA＝∠DCAD．∠B＝∠D＝90°
8．如图，在△ABC中，F是高AD和BE的交点，BC＝6，CD＝2，AD＝BD，则线段AF的长度为（ ）
A．2B．1C．4D．3
二．填空题
9．已知△ABC≌△DEF，∠A＝52°，∠B＝57°，则∠F＝ ．
10．已知△ABC≌△DEF，且△ABC的三边长分别为3cm，4cm，5cm，则△DEF的周长为 cm．
11．如图，已知△ABC≌△ADE，若∠A＝60°，∠B＝40°，则∠BED的大小为 ．
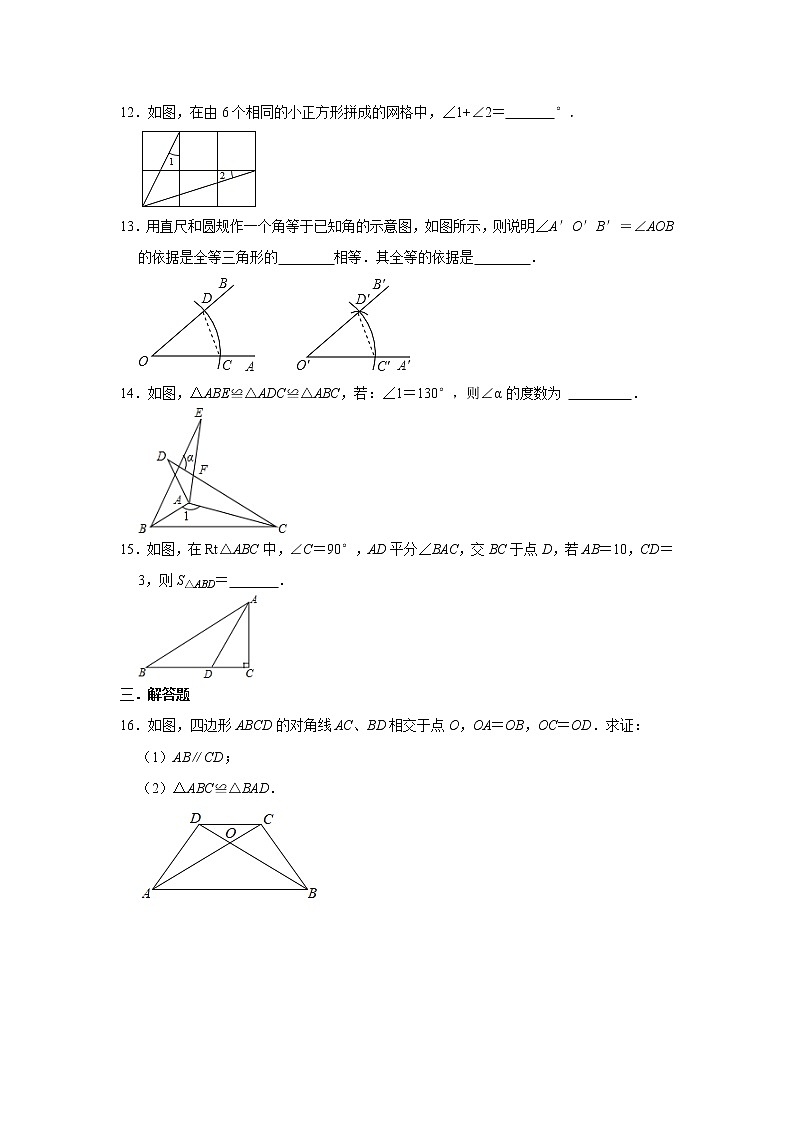
12．如图，在由6个相同的小正方形拼成的网格中，∠1+∠2＝ °．
13．用直尺和圆规作一个角等于已知角的示意图，如图所示，则说明∠A′O′B′＝∠AOB的依据是全等三角形的 相等．其全等的依据是 ．
14．如图，△ABE≌△ADC≌△ABC，若：∠1＝130°，则∠α的度数为 ．
15．如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC，交BC于点D，若AB＝10，CD＝3，则S△ABD＝ ．
三．解答题
16．如图，四边形ABCD的对角线AC、BD相交于点O，OA＝OB，OC＝OD．求证：
（1）AB∥CD；
（2）△ABC≌△BAD．
17．如图，点B、F、C、E在直线l上（F、C之间不能直接测量），点A、D在l异侧，测得AB＝DE，AB∥DE，∠A＝∠D．
（1）求证：△ABC≌△DEF；
（2）若BE＝10m，BF＝3m，求FC的长度．
18．已知：如图，AB＝AC，点D是BC的中点，AB平分∠DAE，AE⊥BE．
（1）求证：AD＝AE．
（2）若BE∥AC，试判断△ABC的形状，并说明理由．
19．已知：在△ABC中，∠ABC＝60°，∠ACB＝40°，BD平分∠ABC，CD平分∠ACB，
（1）如图1，求∠BDC的度数；
（2）如图2，连接AD，作DE⊥AB，DE＝2，AC＝4，求△ADC的面积．
20．如图，∠BAE＝∠CAF＝90°，EC、BF相交于点M，AE＝AB，AC＝AF，
（1）求证：EC＝BF
（2）求证：EC⊥BF
（3）若条件∠BAE＝∠CAF＝90°改为∠BAE＝∠CAF＝m°，则（1）、（2）两个结论还成立吗？结论（1） ，结论（2） （只回答不写过程）．
参考答案
一．选择题
1．解：能够完全重合的两个图形叫做全等形，所以如果两个图形全等，那么这两个图形必定是形状大小均相同．
故选：A．
2．解：∵△ABC≌△DEF，
∴AB＝DE，AC＝DF，BC＝EF，
∴BE＝CF，
故A，B，C正确，
故选：D．
3．解：A、根据SAS可以判定三角形全等，本选项不符合题意．
B、AA不能判定三角形全等，本选项符合题意．
C、根据HL可以判定三角形全等，本选项不符合题意．
D、根据AAS可以判定三角形全等，本选项不符合题意．
故选：B．
4．解：∵△ABC≌△AED，
∴∠AED＝∠B，AE＝AB，∠BAC＝∠EAD，
∴∠1＝∠BAE＝40°，
∴△ABE中，∠B＝＝70°，
∴∠AED＝70°，
故选：A．
5．解：∵△ABC≌△DEF，
∴BC＝EF，
∵BF＝BC﹣FC，CE＝FE﹣FC，
∴BF＝CE，
∵BE＝5，CF＝2，
∴CF＝BE﹣CE﹣BF，即2＝5﹣2BF．
∴BF＝1.5．
故选：C．
6．解：根据题意可得：
在△ABC和△DEC中，
，
∴△ABC≌△DCE（SAS），
∴AB＝DE，
∴依据是SAS，
故选：D．
7．解：A、∵在△ABC和△ADC中
，
∴△ABC≌△ADC（SAS），正确，故本选项错误；
B、根据CB＝CD，AC＝AC，∠BAC＝∠DAC，不能推出△BAC和△DAC全等，错误，故本选项正确；
C、∵在△ABC和△ADC中
，
∴△ABC≌△ADC（ASA），正确，故本选项错误；
D、∵在△ABC和△ADC中
，
∴△ABC≌△ADC（AAS），正确，故本选项错误；
故选：B．
8．证明：∵F是高AD和BE的交点，
∴∠ADC＝∠FDB＝∠AEF＝90°，
∴∠DAC+∠AFE＝90°，
∵∠FDB＝90°，
∴∠FBD+∠BFD＝90°，
又∵∠BFD＝∠AFE，
∴∠FBD＝∠DAC，
在△BDF和△ADC中，，
∴△BDF≌△ADC（AAS），
∴DF＝CD＝2，
∴AD＝BD＝BC﹣DF＝4，
∴AF＝AD﹣DF＝4﹣2＝2；
故选：A．
二．填空题
9．解：∵△ABC≌△DEF，∠A＝52°，∠B＝57°，
∴∠D＝∠A＝52°，∠E＝∠B＝57°，
∴∠F＝180°﹣∠D﹣∠E＝71°，
故答案为：71°．
10．解：∵△ABC的三边长分别为3cm，4cm，5cm，△ABC≌△DEF，
∴△DEF的三边长分别为3cm，4cm，5cm，
∴△DEF的周长为3+4+5＝12（cm），
故答案为：12．
11．解：∵△ABC≌△ADE，
∴∠D＝∠B＝40°，
∴∠BED＝∠A+∠D＝60°+40°＝100°，
故答案为：100°．
12．解：如图所示：
由图可知△ACE与△ABD与△ACF全等，
∴AB＝AC，∠1＝∠CAE＝∠ACF，
∵∠CAE+∠DAC＝90°，
∴∠1+∠DAC＝∠BAC＝90°，
∴△ABC是等腰直角三角形，
∴∠2+∠ACF＝45°，
∴∠1+∠2＝45°，
故答案为：45．
13．解：∠A′O′B′＝∠AOB，
理由是：连接CD、C′D′，
从作图可知OD＝OD′＝OC＝OC′，CD＝C′D′，
∵在△ODC和△O′D′C′中
，
∴△ODC≌△O′D′C′（SSS），
∴∠A′O′B′＝∠AOB（全等三角形的对应角相等），
故答案为：对应角，SSS．
14．解：∵△ABE≌△ADC≌△ABC，
∴∠BAE＝∠1＝130°，∠ACB＝∠E，
∴∠2＝360°﹣∠1﹣∠BAE＝360°﹣130°﹣130°＝100°，
∴∠DFE＝180°﹣∠α﹣∠E，
∠AFC＝180°﹣∠2﹣∠ACD，
∵∠DFE＝∠AFC（对顶角相等），
∴180°﹣∠α﹣∠E＝180°﹣∠2﹣∠ACD，
∴∠α＝∠2＝100°．
故答案为：100°．
15．解：如图，过点D作DE⊥AB于E，
∵∠C＝90°，AD平分∠BAC，
∴DE＝CD＝3，
∴S△ABD＝AB•DE＝×10×3＝15，
故答案为15．
三．解答题
16．（1）证明：∵OA＝OB，OC＝OD，
∴∠OAB＝∠OBA，∠OCD＝∠ODC，
∵∠COD＝∠AOB，∠OAB+∠OBA+∠AOB＝180°，∠OCD+∠ODC+∠COD＝180°，
∴∠OAB＝∠OBA＝∠OCD＝∠ODC，
即∠OAB＝∠OCD，
∴AB∥CD；
（2）∵OA＝OB，OC＝OD，
∴AC＝BD，
在△ABC和△BAD中，
，
∴△ABC≌△BAD（SAS）．
17．（1）证明：∵AB∥DE，
∴∠ABC＝∠DEF，
在△ABC与△DEF中
∴△ABC≌△DEF；
（2）∵△ABC≌△DEF，
∴BC＝EF，
∴BF+FC＝EC+FC，
∴BF＝EC，
∵BE＝10m，BF＝3m，
∴FC＝10﹣3﹣3＝4m．
18．（1）证明：∵AB＝AC，点D是BC的中点，
∴AD⊥BC，
∴∠ADB＝90°，
∵AE⊥AB，
∴∠E＝90°＝∠ADB，
∵AB平分∠DAE，
∴∠BAD＝∠BAE，
在△ADB和△AEB中，，
∴△ADB≌△AEB（AAS），
∴AD＝AE；
（2）解：△ABC是等边三角形．理由如下：
∵BE∥AC，
∴∠EAC＝90°，
∵AB＝AC，点D是BC的中点，
∴∠BAD＝∠CAD＝∠BAE＝30°，
∴∠BAC＝∠BAD+∠CAD＝60°，
∵AB＝AC，
∴△ABC是等边三角形．
19．解：（1）∵BD平分∠ABC，
∴∠DBC＝∠ABC＝×60°＝30°，
∵CD平分∠ACB，
∴∠DCB＝∠ACB＝×40°＝20°，
∴∠BDC＝180°﹣∠DBC﹣∠DCB
＝180°﹣30°﹣20°
＝130°；
（2）作DF⊥AC于F，DH⊥BC于H，如图2，
∵BD平分∠ABC，DE⊥AB，DH⊥BC，
∴DH＝DE＝2，
∵CD平分∠ACB，DF⊥AC，DH⊥BC，
∴DF＝DH＝2，
∴△ADC的面积＝DF•AC＝×2×4＝4．
20．证明：（1）∵AE⊥AB，AC⊥AF，
∴∠BAE＝∠CAF＝90°，
∴∠CAE＝∠BAF，
在△CAE与△BAF中，
，
∴△CAE≌△BAF，
∴CE＝BF；
（2）如图，设AC交BF于O．
∵△CAE≌△BAF，
∴∠AFO＝∠OCM，
∵∠AOF＝∠COM，
∴∠OMC＝∠OAF＝90°，
∴CE⊥BF．
（3）条件∠BAE＝∠CAF＝90°改为∠BAE＝∠CAF＝m°，则结论（1）成立，结论（2）不成立．
理由：同法可证△CAE≌△BAF，可得CE＝BF，∠CMO＝∠FAO＝m°，
∴结论（1）成立，结论（2）不成立．
故答案为成立，不成立．