高中数学4.4 对数函数导学案

4.4.2对数函数的图象与性质

【学习目标】

1.会用描点法画出具体对数函数的图象，了解对数函数的图象特征、单调性与特殊点；

2.知道对数函数与指数函数互为反函数；

3.会用对数函数的图象与性质解决简单问题．

【自主学习】

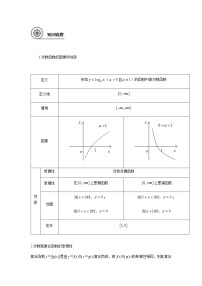
一、对数函数的图像与性质

二、反函数

1.概念

设函数的定义域为，值域为B，从式子中解出，得式子．如果对于在B中的任何一个值，通过式子，在中都有唯一确定的值和它对应，那么式子表示是的函数，函数叫做函数的反函数，记作        ，习惯上改写成．

2.性质

（1）原函数与反函数的图象关于直线      对称．

（2）函数的定义域、值域分别是其反函数的      、      ．

（3）若在原函数的图象上，则点      在反函数的图象上．

（4）一般地，函数要有反函数则它必须为单调函数．

【小试牛刀】

1.在同一直角坐标系中画出函数和的图象，并说明它们的关系.

2.比较下列各题中两个值的大小：

（1）；   （2）；   （3）.

3.某地去年的GDP（国内生产总值）为3000亿元人民币，预计未来5年的平均增长率为6.8%.

（1）设经过年达到的年GDP为亿元，试写出未来5年内，关于的函数解析式；

（2）经过几年该地GDP能达到3900亿元人民币？

4.求下列函数的定义域：

（1）；    （2）.

5.判断下列各对函数是否互为反函数.若是，则求出它们的定义域和值域：

（1），；   （2），.

6.已知 ，，，求实数的取值范围.

【答案】

1.图象略，函数和的图象关于轴对称.

2.（1）；           （2）；

（3）当时，；当时，.

3.（1）； （2）4年.

4.（1）；   （2）.

5（1）互为反函数，的定义域是，值域是R，的定义域是R，值域是；

（2）互为反函数，定义域是，值域是R，的定义域是R，值域是.

6..