高中数学苏教版 (2019)必修 第一册第4章 指数与对数4.2 对数导学案
展开1、掌握对数函数的图象和性质,培养学生实际应用函数的能力;
2、通过观察图象,分析、归纳、总结对数函数的性质;
3、在对数函数的学习过程中,体验数学的科学价值并养成勇于探索的良好习惯.
1.数学抽象:对数函数的图像与性质;
2.逻辑推理:图像平移问题;
3.数学运算:求函数的定义域与值域;
4.数据分析:利用对数函数的性质比较两个函数值的大小及解对数不等式;
5.数学建模:通过由抽象到具体,由具体到一般的数形结合思想总结指数函数性质.
重点:对数函数的图象和性质;
难点:对底数的分类,如何由图象、解析式归纳对数函数的性质.
预习导入
阅读课本132-133页,填写。
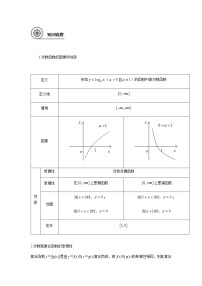
1.对数函数的图象及性质
[点睛] 底数a与1的大小关系决定了对数函数图象的“升降”:当a>1时,对数函数的图象“上升”;当0<a<1时,对数函数的图象“下降”.
2.反函数
指数函数__________和对数函数y=lgax(a>0且a≠1)互为反函数.
1.若函数y=lgax的图象如图所示,则a的值可能是 ( )
A.0.5B.2C.eD.π
2.下列函数中,在区间(0,+∞)内不是增函数的是( )
A.y=5xB.y=lg x+2 C.y=x2+1 D.y=
3.函数的f(x)=lga(x-2)-2x的图象必经过定点 ..
4.(1)函数f(x)= 的反函数是 .
(2)函数g(x)=lg8x的反函数是 .
题型一 对数函数的图象
例1 函数y=lg2x,y=lg5x,y=lg x的图象如图所示.
(1)说明哪个函数对应于哪个图象,并说明理由;
(2)在如图的平面直角坐标系中分别画出y=lg12x,y=lg15x,y=lg110x的图象;
(3)从(2)的图中你发现了什么?
跟踪训练一
1、作出函数y=|lg(x-1)|的图象,并根据图象写出函数的定义域、值域以及单调区间.
题型二 比较对数值的大小
例2 比较下列各组数中两个值的大小:
(1)lg23.4,lg28.5;
(2)lg0.31.8,lg0.32.7;
(3)lga5.1,lga5.9(a>0,且a≠1).
跟踪训练二
1.比较下列各题中两个值的大小:
(1)lg 6,lg 8; (2)lg0.56,lg0.54;
(3)lg2与lg2; (4)lg23与lg54.
题型三 比较对数值的大小
例3 (1)已知lgaeq \f(1,2)>1,求a的取值范围;
(2)已知lg0.7(2x)<lg0.7(x-1),求x的取值范围.
跟踪训练三
1.已知lga(3a-1)恒为正,求a的取值范围.
题型四 有关对数型函数的值域与最值问题
例4 求下列函数的值域.
(1)y=lg2(x2+4);(2)y=lg (3+2x-x2).
跟踪训练四
1.已知f(x)=2+lg3x,x∈[1,9],求函数y=[f(x)]2+f(x2)的最大值及此时x的值.
1.若lg(2x-4)≤1,则x的取值范围是( )
A.(-∞,7] B.(2,7]
C.[7,+∞) D.(2,+∞)
2.已知lgm<lgn<0,则( )
A.n<m<1 B.m<n<1
C.1<m<n D.1<n<m
3.函数f(x)=|lgx|的单调递增区间是( )
A.eq \b\lc\(\rc\](\a\vs4\al\c1(0,\f(1,2))) B.(0,1]
C.(0,+∞) D.[1,+∞)
4.已知实数a=lg45,b=eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))0,c=lg30.4,则a,b,c的大小关系为( )
A.b<c<a B.b<a<c
C.c<a<b D.c<b<a
5.函数f(x)=lgeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,\r(x2+1)+x)))是( )
A.奇函数 B.偶函数
C.既奇又偶函数 D.非奇非偶函数
6.比较大小:
(1)lg22______lg2eq \r(3);
(2)lg3π______lgπ3.
7.不等式lg (5+x)
答案
小试牛刀
1-2.AD
3.(3,-6)
4.(1)f(x)=lg23x (2)g(x)=8x
自主探究
例1 【答案】见解析
【解析】(1)①对应函数y=lg x,②对应函数y=lg5x,③对应函数y=lg2x.这是因为当底数全大于1时,在x=1的右侧,底数越大的函数图象越靠近x轴.
(2)在题图中的平面直角坐标系中分别画出y=lg12x,y=lg15x,y=lg110x的图象如图所示.
(3)从(2)的图中可以发现:y=lg x与y=lg110x,y=lg5x与y=lg15x,y=lg2x与y=lg12x的图象分别关于x轴对称.
跟踪训练一
1、【答案】其定义域为(1,+∞),值域为[0,+∞),单调递减区间为(1,2],单调递增区间为(2,+∞).
【解析】先画出函数y=lg x的图象(如图①).
再将该函数图象向右平移1个单位长度得到函数y=lg(x-1)的图象(如图②).
图① 图② 图③
最后把y=lg(x-1)的图象在x轴下方的部分对称翻折到x轴上方(原来在x轴上方的部分不变),即得出函数y=|lg(x-1)|的图象(如图③).
由图易知其定义域为(1,+∞),值域为[0,+∞),单调递减区间为(1,2],单调递增区间为(2,+∞).
例2 【答案】(1) lg23.4<lg28.5 (2) lg0.31.8>lg0.32.7 (3)当a>1时,lga5.1<lga5.9;当0<a<1时,lga5.1>lga5.9.
【解析】(1)考察对数函数y=lg2x,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是lg23.4<lg28.5.
(2)考察对数函数y=lg0.3x,因为它的底数0<0.3<1,所以它在(0,+∞)上是减函数,于是lg0.31.8>
(3)当a>1时,y=lgax在(0,+∞)上是增函数,于是lga5.1<lga5.9;
当0<a<1时,y=lgax在(0,+∞)上是减函数,于是lga5.1>lga5.9.
跟踪训练二
1.【答案】(1)lg 6<lg 8(2)lg0.56<lg 0.54(3)lg2
(2)因为函数y=lg0.5x在(0,+∞)上是减函数,且6>4,所以lg0.56<lg 0.54.
(3)由于lg2=eq \f(1,lg2\f(1,3)),lg2=eq \f(1,lg2\f(1,5)).
又∵对数函数y=lg2x在(0,+∞)上是增函数,且eq \f(1,3)>eq \f(1,5),
∴0>lg2 eq \f(1,3)>lg2 eq \f(1,5),∴eq \f(1,lg2\f(1,3))<eq \f(1,lg2\f(1,5)).
∴lg2
∵lg23>lg22=1=lg55>lg54,∴lg23>lg54.
例3【答案】(1)eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),1)); (2) (1,+∞).
【解析】(1)由lgaeq \f(1,2)>1得lgaeq \f(1,2)>lgaa.
①当a>1时,有a<eq \f(1,2),此时无解.
②当0<a<1时,有eq \f(1,2)<a,从而eq \f(1,2)<a<1.
∴a的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2),1)).
(2)∵函数y=lg 0.7x在(0,+∞)上为减函数,
∴由lg0.72x<lg0.7(x-1)
得eq \b\lc\{\rc\ (\a\vs4\al\c1(2x>0,,x-1>0,,2x>x-1,))解得x>1.
∴x的取值范围是(1,+∞).
跟踪训练三
1.【答案】eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3),\f(2,3)))∪(1,+∞)
【解析】由题意知lga(3a-1)>0=lga1.
当a>1时,y=lgax是增函数,
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(3a-1>1,,3a-1>0,))解得a>eq \f(2,3),∴a>1;
当0<a<1时,y=lgax是减函数,
∴eq \b\lc\{\rc\ (\a\vs4\al\c1(3a-1<1,,3a-1>0,))解得eq \f(1,3)<a<eq \f(2,3).∴eq \f(1,3)<a<eq \f(2,3).
综上所述,a的取值范围是eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,3),\f(2,3)))∪(1,+∞).
例4 【答案】(1) [2,+∞); (2)[-2,+∞).
【解析】(1)y=lg2(x2+4)的定义域是R.
因为x2+4≥4,所以lg2(x2+4)≥lg24=2,
所以y=lg2(x2+4)的值域为[2,+∞).
(2)设u=3+2x-x2=-(x-1)2+4≤4.
因为u>0,所以0<u≤4.
又y=lgu在(0,+∞)上为减函数,
所以lgu≥lg4=-2,
所以y=lg (3+2x-x2)的值域为[-2,+∞).
跟踪训练四
1.【答案】当x=3时,y取得最大值,为13.
【解析】y=[f(x)]2+f(x2)=(2+lg3x)2+lg3x2+2=(lg3x)2+6lg3x+6=(lg3x+3)2-3.
∵f(x)的定义域为[1,9],
∴y=[f(x)]2+f(x2)中,x必须满足eq \b\lc\{\rc\ (\a\vs4\al\c1(1≤x≤9,,1≤x2≤9,))
∴1≤x≤3,∴0≤lg3x≤1,∴6≤y≤13.
∴当x=3时,y取得最大值,为13.
当堂检测
1-5.BDDDA
6.(1)> (2)>
7.{x|-2
【解析】要使y=lg (1-x2)有意义,则1-x2>0,
∴x2<1,则-1<x<1,因此函数的定义域为(-1,1).
令t=1-x2,x∈(-1,1).
当x∈(-1,0]时,x增大,t增大,y=lgt减小,
∴x∈(-1,0]时,y=lg (1-x2)是减函数;
同理当x∈[0,1)时,y=lg (1-x2)是增函数.
故函数y=lg (1-x2)的单调增区间为[0,1),且函数的最小值ymin=lg (1-02)=0.
a的范围
0<a<1
a>1
图 象
a的范围
0<a<1
a>1
性质
定义域
__________
值域
R
定点
__________,即x=_______时,y=_________
单调性
在(0,+∞)上是__________
在(0,+∞)上是__________
高中人教A版 (2019)4.4 对数函数第2课时学案: 这是一份高中人教A版 (2019)4.4 对数函数第2课时学案,文件包含正文docx、答案docx等2份学案配套教学资源,其中学案共14页, 欢迎下载使用。
人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数第1课时学案设计: 这是一份人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数第1课时学案设计,文件包含正文docx、答案docx等2份学案配套教学资源,其中学案共10页, 欢迎下载使用。
人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数导学案及答案: 这是一份人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数导学案及答案,共2页。