3.1.1函数的概念及其表示方法

这是一份3.1.1函数的概念及其表示方法，文件包含第1课迎接蚕宝宝的到来pptx、第1课迎接蚕宝宝的到来docx、为蚕建造一个家mp4、蚕的孵化mp4、观察蚕卵的样子mp4等5份课件配套教学资源，其中PPT共31页， 欢迎下载使用。

1.函数的概念
(1)函数的定义：
一般地，设是两个非空的数集，如果按照某种确定的对应关系，使对于集合中的任意一个数，在集合中都有唯一确定的数和它对应；那么就称为从集合到集合的一个函数．记作，.
(2)函数的定义域、值域：
在函数，中，叫做自变量，的取值范围叫做函数的定义域；与的值相对应的值叫做函数值，函数值的集合叫做函数的值域．显然，值域是集合的子集．
（3）函数的四个特征：
ⅰ）非空性：函数定义中的集合必须是两个非空集合并且是数集.如，就不是函数（定义域为空集）；
ⅱ）任意性：中任意一个数都要考虑到，即中每一个元素都有函数值；
ⅲ）唯一性：每一个自变量都有唯一的函数值与之对应；
ⅳ）方向性：函数是从一个定义域到值域的对应关系，如果改变这个对应方向，那么新的对应关系就不一定是函数.
题型1：函数的判断
1.判断对应关系是不是集合到集合的函数的方法，主要看三个方面：
（1）必须是非空数集；
（2）中任何一个元素在中必须有元素与其对应；
（3）中任何一个元素在中的对应关系是唯一性（一对一或者多对一）.
例1：下列对应关系是集合A到集合B的函数的为
，对应关系如图所示：
例2．下列图形中，不可能是函数图象的是（ ）
A．B．C．D．
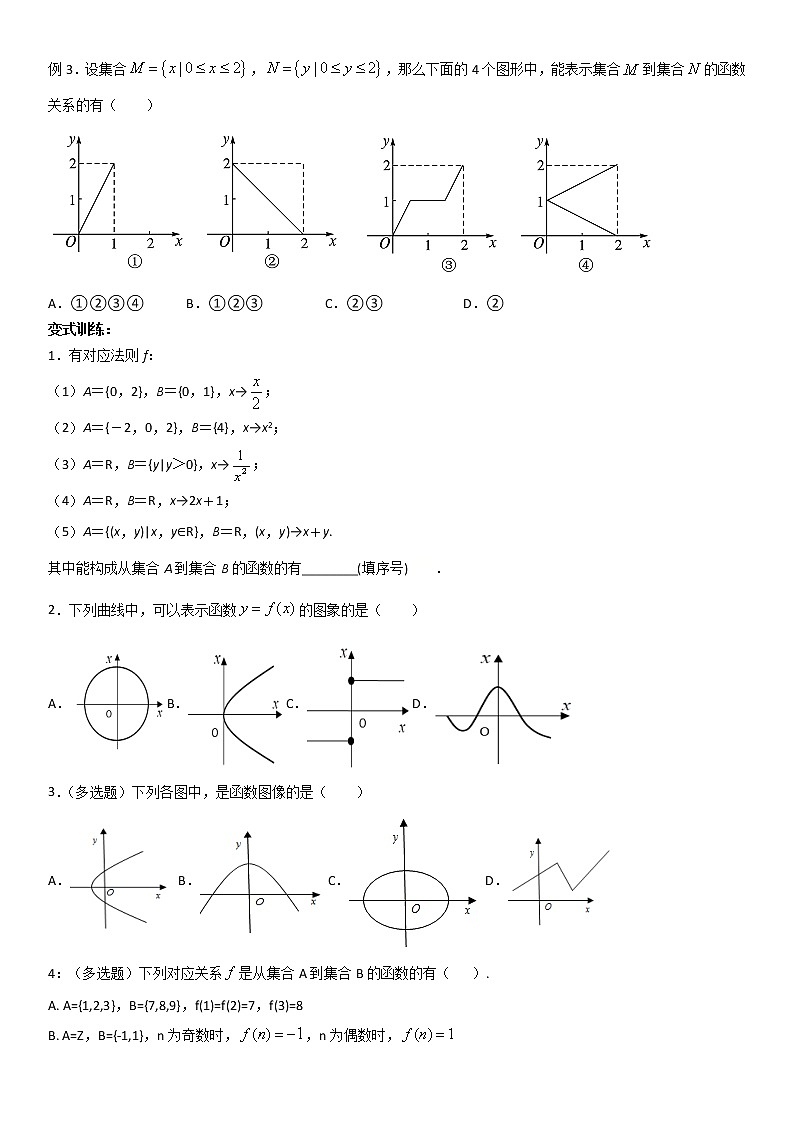
例3．设集合，，那么下面的4个图形中，能表示集合到集合的函数关系的有（ ）
A．①②③④B．①②③C．②③D．②
变式训练：
1．有对应法则f：
（1）A＝{0，2}，B＝{0，1}，x→；
（2）A＝{－2，0，2}，B＝{4}，x→x2；
（3）A＝R，B＝{y|y＞0}，x→；
（4）A＝R，B＝R，x→2x＋1；
（5）A＝{(x，y)|x，y∈R}，B＝R，(x，y)→x＋y.
其中能构成从集合A到集合B的函数的有________(填序号)．
2．下列曲线中，可以表示函数的图象的是（ ）
A．B．C．D．
3．（多选题）下列各图中，是函数图像的是（ ）
A．B．C．D．
4：（多选题）下列对应关系是从集合A到集合B的函数的有（ ）.
A={1,2,3}，B={7,8,9}，f(1)=f(2)=7，f(3)=8
A=Z，B={-1,1}，n为奇数时，，n为偶数时，
A=B={1,2,3}，
A=B=
题型二：函数求值
（1）已知函数解析式求函数值，可分别将自变量的值代入解析式即可求出相应的函数值，若自变量的值包含字母的代数式时，可将代数式整体代入即可.
（2）已知函数解析式，求对应函数值的自变量（或解析式中参数值），只需将函数值代入解析式，建立方程即可求解.
例1：已知
求和
求
若，求.
例2：已知函数，且，则实数＝________.
变式训练：
已知，则______.
已知函数.
（1）求与，与的值．
（2）由（1）中求得的结果，你能发现与有什么关系？并证明你的发现．
（3）求的值
3. 若，，则________
知识点2：函数的三要素
由函数的概念知，一个函数的构成要素为定义域、对应关系和值域.
（1）定义域：函数的定义域就是自变量的取值范围.有时函数的定义域可以省略不写，如果为特殊说明，函数的定义域是指能使表达函数的式子各部分都有意义的所有实数的集合.
（2）对应关系：对应关系是函数的核心，它是对自变量实施“对应操作”的“程序”或“方法”，按照这一“程序”,从定义域中任取一个，可在值域中找到唯一的与之对应，同一“”可以“操作”不同形式的变量.
（3）值域：对于定义域内函数，其值域就是指集合.
题型一；求函数的定义域
已知函数的解析式求函数的定义域
如果是分式，定义域为分母不为零的实数集合；
如果是偶次根式，定义域为被开方数不小于零的实数集合；
的定义域为；
如果是由几个代数式通过四则运算构成的，定义域为各部分分别有意义的集合的公共部分.
例1.求下列函数的定义域
（1） （2）
变式训练
求下列函数的定义域
函数的定义域是
（2）函数的定义域是
（3）函数的定义域为______.
求抽象函数（复合函数）的定义域
（1）复合函数定义：两个或两个以上的基本初等函数经过嵌套式复合成一个函数叫做复合函数.
（2）复合函数形式：，令：，则转化为其中叫作中间变量.叫作内层函数，叫作外层函数.
（3）求复合函数（抽象函数）的定义域应明确以下三点
①函数的定义域是指的取值范围所组成的集合
②求函数的定义域，应是求的取值范围，而不是求的取值范围
③三个函数中的在相同的对应关系下的范围相同.
例1.（1）若函数的定义域为，则函数的定义域
（2）若函数的定义域为，则函数的定义域
（3）若函数的定义域为，则函数的定义域
（4）已知函数，则函数的定义域是
变式训练：
1．求下列函数定义域
（1）已知函数的定义域为，求的定义域.
（2）已知函数的定义域为，求的定义域
（3）已知函数的定义域为，求的定义域.
（4）设函数的定义域为，则的定义域.
（5）若的定义域为，求的定义域
函数定义域的逆运算
已知函数的定义域，逆向求解函数中参数的取值，需运用分类讨论以及转化与化归的方法，这种思想方法是通过某种转化过程，将一个难以解决的问题转化为一个已经解决或者容易解决的问题.
已知函数的定义域为，则实数的取值范围。
例2.已知函数的定义域为[-3,6]，则的值为 ,的值为 .

变式训练：
例1.已知函数的定义域为R，则实数的值为 .
2.已知函数在上有意义，则实数的范围。
知识点3：函数的相等
判断两个函数是否为同一个函数的方法：
（1）一看定义域，二看对应关系，若定义域和对应关系有一个不同，则不是同一个函数
（2）若定义域相同，对应关系一致，则是同一个函数.
例1：下列表示同意函数的是（ ）
A. B.
C. D.
例2.与表示同一函数的是（ ）

，
变式训练：
1.下列各组函数是同一函数的是（ ）
（1）；（2）
（3） （4）

2．（多选题）下列各组函数是同一组函数的是（ ）
A．与B．与
C．与D．与
基础巩固
1．函数的定义域是（ ）
A．B．C．D．
2．图中给出的四个对应关系，其中构成函数的是（ ）
① ② ③ ④
A．①②B．①④C．①②④D．③④
3．已知，求______．
4．已知等腰三角形的周长为40，设其底边长为ycm，腰长为xcm.则函数的定义域为（ ）
A．B．C．D．
5．若， ，则（ ）
A．B．C．D．
6．托马斯说：“函数概念是近代数学思想之花.”请根据函数的概念判断：下列对应是集合到集合的函数的是（ ）
A．B．C．D．
7．若，则等于（ ）
A．3B．C．4D．
8．已知函数，则__________．
9．若函数的定义域为，则实数的取值范围是______．
10．已知函数的定义域为，则的定义域是（ ）
A． B． C．D．
能力提升
二、多选题
11．在下列四组函数中，与表示同一函数的是（ ）
A．，B．，
C．，D．，
12．下列各图中，可能是函数图象的是（ ）
A．B．C．D．
三、解答题
13．已知函数．
（1）求，的值；
（2）求证：是定值；
（3）求的值．
14．（1）已知的定义域为，求函数的定义域；
（2）已知的定义域为，求的定义域；
（3）已知函数的定义域为，求函数的定义域．
参考答案
1．C
2．B
3．4
4．A
5．A
6．C
7．B
8．1
9．
10．D
11．BD
12．ACD
13．（1），；（2）证明见解析；（3）2019.
【详解】
（1）
，；
（2）证明：，是定值；
（3）
．
14．（1）；（2）；（3）. 第二课时 求函数的值域及函数表示方法
知识点1.求函数值域，
首先必须先求函数的定义域；再根据解析式的结构特点，选择适当的方法，常用的方法有：
观察法：对于一些简单的函数，其值域可通过观察得到.
配方法：它是求“二次函数型函数”值域的基本方法，或的函数的值域问题，均可使用配方法.
例1.求下列函数的值域
. （2） （3）
利用常见函数的值域：
①一次函数的值域为R；
②二次函数利用配方法，结合定义域和开口求出值域；
③反比例函数的值域为；
分离常数法：即将有理分式（形如，）转化为“反比例函数类”的形式，便于求值域.
例1： 求下列函数的值域 （1） （2）
（4）换元法：对于一些无理函数（如），通过换元把它们转化为有理函数，然后通过求有理函数的值域间接地求解原函数的值域.
例1：求下列函数的值域（1） （2）
判别式法：形如把函数转化为关于x的一元二次方程，用Δ来求y的范围。
函数的值域为 . 求函数的值域
变式训练：
1．求下列函数的值域
（1）； （2）； （3）；
（4）； （5） （6）；
6.若为实数，则函数的值域为（ ）

函数值域的逆向问题
已知函数的值域求参数问题的解题思路
根据值域的定义将给出的值域转化为方程的解或不等式的解集的问题
根据方程的解或不等式的解集情况来确定参数的值或取值范围
例1：已知函数的定义域为R，值域为[1,9]，则m的值为 ;n的值为 .

变式训练
1.若函数的值域为，求实数的值
知识点2：函数的表示方法
题型一.列表法及图像法的应用
例1．已知函数f(x)，g(x)分别由下表给出：
则（ ）
A．0B．1C．2D．3
2．下表表示y是x的函数，则函数的值域是（ ）
A．B．C．D．
3．某学校高中部举行秋季田径运动会，甲、乙、丙、丁位同学代表高一（1）班参加男子组米接力跑比赛，甲同学负责跑第二棒.在比赛中，从甲接到接力棒到甲送出接力棒，甲同学的跑步速率（单位：）关于跑步时间（单位：）的函数图象最可能是（ ）
A．B．C．D．
变式训练：
1．已知函数的定义域为，且自变量x与函数值的关系对应如下表：
（1）_______．
（2）不等式的解集为_______．
2．已知函数分别由下表给出，则满足的为（ ）
A．0B．1C．2D．3
3．某同学骑自行车上学，开始时匀速行驶，途中因红灯停留了一段时间，然后加快速度赶到了学校，下列各图中，符合这一过程的是（ ）
A．B．C．D．
4．（多选题）水滴进玻璃容器，如图所示（设单位时间内进水量相同），那么水的高度是如何随时间变化的？下列匹配的图象与容器符合实际的有（ ）
Ⅰ——（2）B．Ⅱ——（1）C．Ⅲ——（3）D．Ⅴ——（4）
题型二.函数解析式的求法
1.代入法：已知的解析式，求的解析式，常用代入法.
例1.已知，求的解析式
1.，求的解析式为
2.待定系数法：若已知函数类型（一次函数，二次函数，反比函数），可用待定系数法求解，先设出，然后利用题目中的已知条件，列出关于待定系数的方程组，进而求出待定的系数.
例1.（1）已知一次函数满足，则的解析式为

（2）已知二次函数满足，则的解析式为
变式训练：1. 已知是一次函数，且满足，则的解析式为
2.已知是二次函数，且.则的解析式为
3.换元法(配凑法):主要解决已知复合函数表达式，求解的解析式的问题.
(1)配凑法是将右端的代数式配凑成关于的形式，再将解析式两边的用代替即可,进而求出的解析式.
(2)换元法是令解出用来表示（注意新元的范围），即用表示，然后代入中即可求出的解析式，最后用代替的解析式知所有的即可.
例1.（1）已知，则的解析式
（2）已知，则的解析式
变式训练 1.已知，则的解析式为
2.已知，则的解析式为
4.构造方程组法(消元法）：已知中含有或的形式的式子，求的解析式，
例1.（1）已知函数满足，则函数的解析式为

（2）已知函数满足，则函数的解析式为
变式训练：1.已知函数满足，则函数的解析式为
2.已知，则函数的解析式为
5.求抽象函数的解析式：
赋值法求函数的解析式：当所给的函数中含有两个变量时，可对这两个变量交替用特殊值代入，或使这两个变量相等代入，再根据已知条件求出函数解析式，具体取什么特殊值，要根据题目特征而定.
例1 .设是上的函数，且满足，并且对任意的实数都有
，则函数的解析式为
基础巩固
1．函数的值域为（ ）
A．B．C．D．
2．已知函数，用列表法表示如下：
则（ ）
A．B．0C．2D．3
3．某同学到长城旅游，他骑行共享单车由宾馆前往长城，前进了，疲意不堪，休息半小时后，沿原路返回，途中看见路边标语“不到长城非好汉”，便调转车头继续向长城方向前进，则该同学离起点(宾馆)的距离s与时间t的函数图象大致为（ ）
A． B． C．D．
4．下列函数中，值域为的函数是（ ）
A．B．C．D．
5．函数的值域为_____．
6．函数的值域是（ ）
A．B．C．D．
7．若函数的定义域和值域都是，则（ ）
A．1B．3C．D．1或3
8．已知集合，，则（ ）
A．B．
C．D．
9．（多选题）已知函数是一次函数，满足，则的解析式可能是（ ）
A．B．C．D．
10．已知函数，，
（1）求，的值；
（2）求满足的的值；
（3）求函数的解析式及定义域.
11．（1）已知求的解析式.
（2）已知函数，求函数，的解析式
（3）已知是二次函数，且，求的解析式
（4）已知函数满足，则=_____________.
能力提升
12．函数的值域为___________.
13．已知函数，则的最小值为______．
14．若函数，满足，且，则________．
15．已知函数可表示为（ ）
则下列结论正确的是（ ）
A．B．的值域是
C．的值域是D．在区间上单调递增
16．如图，是边长为2的正三角形，记位于直线≤左侧的图形的面积为，则的大致图像为（ ）
A．B．C．D．
17．设函数满足，且对任意，都有，则=_________.
18．若，，求函数的值域________.
三、多选题
19．知函数满足，则关于函数正确的说法是（ ）
A．的定义域为B．值域为，且
C．在单调递减D．不等式的解集为
四、解答题
20．在下列问题中任选其中二个解答.
（1）已知函数，求的解析式；
（2）已知一次函数满足，求的解析式；
（3）求函数的值域；
（4）求函数的值域.
参考答案
1．A
【详解】因为为减函数，所以，
故函数值域为.故选：A
2．D
【详解】由表格可得：，所以，所以故选：D
3．C
【详解】
第一段时间，该同学骑行共享单车由宾馆往长城方向，前进了，则该同学离起点(宾馆)的距离s与时间t的函数图象应是直线，且单调递增；
第二段时间休息了半小时，随时间变化，该同学离起点的距离并没有发生变化，因此该同学离起点(宾馆)的距离s与时间t的函数图象应是一条横线；
第三段时间，原路返回，其距离起点应越来越近，因此该同学离起点(宾馆)的距离s与时间t的函数图象应是直线，且单调递减；
第四段时间，调转车头继续向长城方向前进，该部分对应的图象应和第一段时间的相似；因此只有C选项符合.
4．C【详解】
对于A中，根据一次函数的性质，可得函数的值域为，不符合题意；
对于B中，根据二次函数的性质，可得函数的值域为，不符合题意；
对于C中，根据幂函数的性质，可得函数的值域为，符合题意；
对于D中，由函数，可得其定义域为，
由，可得函数的值域，不符合题意.故选：C.
5．
【详解】
函数，
可以看作是将函数向右平移2个单位，再向上平移3个单位，因为函数的值域为所以原函数的值域为.故答案为：.
6．B
【详解】由题意，函数的对称轴且开口向上，
所以函数在区间上单调递减，在区间上单调递增，
所以当时，函数取得最小值，最小值为，
又由，所以函数的最大值为，
所以函数的值域为．故选：B．
7．B
【详解】因为函数在上为增函数，且定义域和值域都是，
所以，，解得或（舍），故选：B
8．B
【详解】因为，所以，解得或，则集合或，因为，所以集合，则，故选：B.
9．AD
【详解】设()，
则，∴，
解得或，∴或.故选：AD.
10．（1），；（2）；
（3）的解析式及定义域为.
【详解】
（1）函数，，
所以，，.
（2）由得，即.
（3），，
所以， ，
即，
由可得，当时，，当时，，
可得符合条件的值域为：
，所以，是合理的，
综上所述函数的解析式及定义域为.
11．（1），；（2）；；（3）；（4）.
【详解】
（1）令，当时，，当且仅当时，等号成立；
当时，，当且仅当时，等号成立；
所以；
又，所以，，
因此，；
（2）令，因为，所以，即；
所以；
（3）设二次函数，
因为，
所以，
即，即，
因此，解得，所以；
（4）因为函数满足①，
所以②，
②①可得：，
整理得.
12．
【详解】
，因为，所以.故答案为：．
13．
【详解】
令t＝＋2，则x＝(t－2)2.由于x≥0，所以t≥2.
则
所以,当时，，故答案为：
14．
【详解】由，可知，联立可得，所以，又因为，所以，所以.
故答案为：
15．B
【详解】
A. ，所以该选项错误；
B. 由表得的值域是，所以该选项正确；
C. 由表得的值域是，不是，所以该选项错误；
D. 在区间上不是单调递增，如：，但是，所以该选项错误.故选：B
16．B
【详解】
因为是边长为2的正三角形，
当≤1时， ；
当≤2时，
所以.只有选项B中图像符合
故选：B.
17．2021
【详解】
令，得，
令得，即，
所以，
所以，故答案为：2021
18．
【详解】
要使函数成立，则，即，将函数代入得：
，令，则，所以，又或，
故函数的值域为.
故答案为：.
19．BCD
【分析】
求出解析式，根据函数解析式逐一判断即可.
【详解】
由于，故（且），
所以的定义域为且，故A不正确；
作出其图象，由图象知：由于，故值域为，且；
在单调递减；的解集为.
故选：BCD
20．（1）；（2）或；（3）；（4）
【分析】
（1）令，将代入已知即可求出；
（2）设，利用已知建立关系求出即可；
（3）将函数解析式转化为关于的方程，利用方程有解即可.
（4）令，可得，利用二次函数的性质即可求解.
【详解】
（1）令，则，
，
；
（2）设，
则，
，解得或，
或；
（3），函数定义域为，
可化为，
则该方程有实数根，，
解得，故函数值域为；
（4）令，则，且，
则函数等价于，
则当时，函数取得最小值为，
故该函数的值域为.
x
1
2
3
f(x)
2
1
1
x
1
2
3
g(x)
3
2
1
x
y
1
0
1
x
1
2
3
4
3
2
1
2
x
0
1
2
y
1
0
2
1
2
3
4