初中人教版23.2.1 中心对称测试题

这是一份初中人教版23.2.1 中心对称测试题，共5页。试卷主要包含了2《中心对称》课时练习等内容，欢迎下载使用。

一、选择题
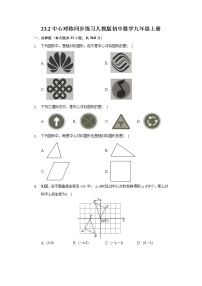
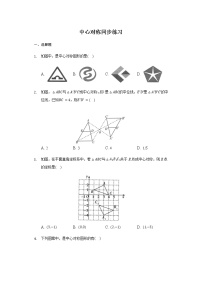
观察下列图形，是中心对称图形的是（ ）
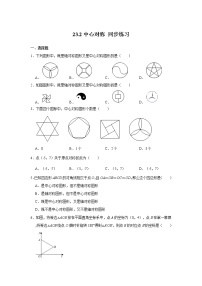
观察下列图案，既是中心对称图形又是轴对称图形的是（ ）

下列汉字或字母中既是中心对称图形又是轴对称图形的是（ ）
A. B. C. D.
下列图形，可以看作中心对称图形的是( )
A． B． C． D．
在直角坐标系中，点A的坐标为（﹣3，4），那么下列说法正确的是（ ）
A.点A与点B（﹣3，﹣4）关于y轴对称
B.点A与点C（3，﹣4）关于x轴对称
C.点A与点C（4，﹣3）关于原点对称
D.点A与点F（﹣4，3）关于第二象限的平分线对称
下列各点中关于原点对称的两个点是（ ）
A．（﹣5，0）和（0，5）B．（2，﹣1）和（1，﹣2）
C．（5，0）和（0，﹣5）D．（﹣2，﹣1）和（2，1）
如图，已知△ABC与△CDA关于点O对称，过O任作直线EF分别交AD，BC于点E，F.
下面的结论：①点E和点F，点B和点D是关于中心O的对称点；
②直线BD必经过点O；
③四边形ABCD是中心对称图形；
④四边形DEOC与四边形BFOA的面积必相等；
⑤△AOE与△COF成中心对称.
其中正确的个数为( )
A.2个 B.3个 C.4个 D.5个
如图所示，已知△ABC和△A＇B＇C＇关于点O成中心对称，则下列结论错误的是（ ）
A.∠ABC=∠A＇B＇C＇ B.∠AOC=∠A＇OC＇ C.AB=A＇B＇ D.OA=OC＇
如图，为保持原图的模样，应选哪一块拼在图案的空白处( )
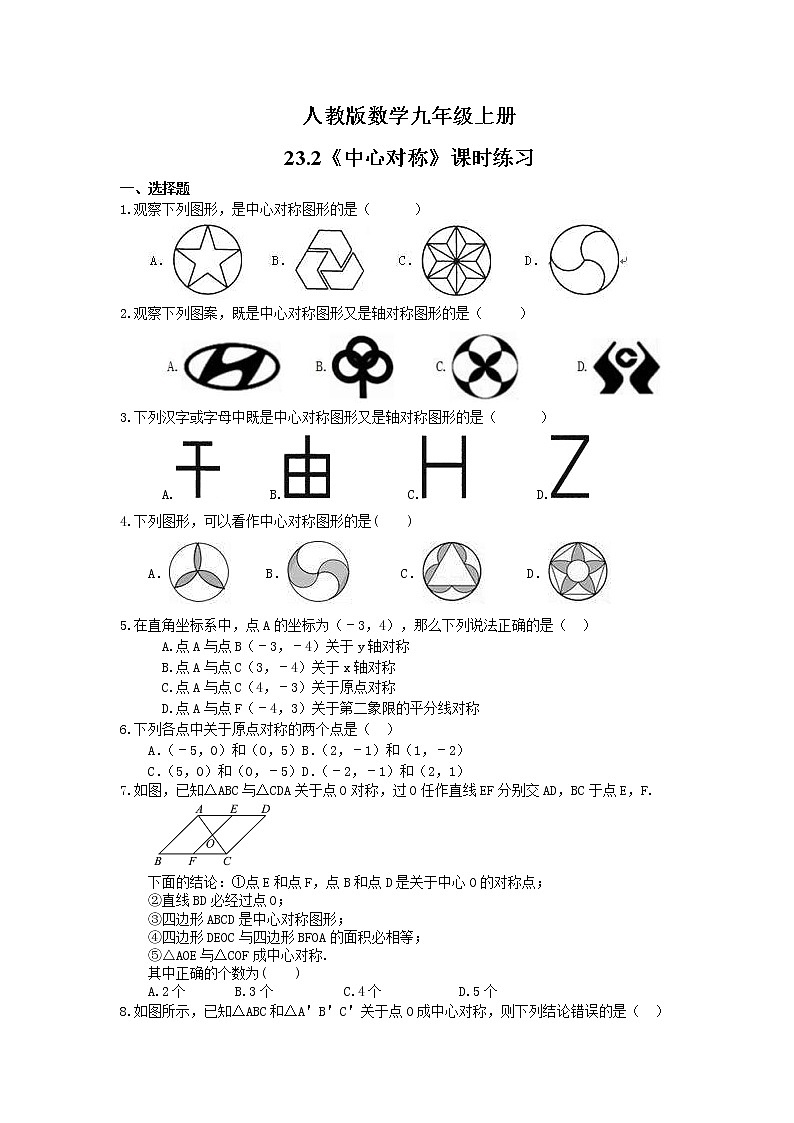
如图，在4×4的正方形网格中，每个小正方形的顶点称为格点，左上角阴影部分是一个以格点为顶点的正方形（简称格点正方形）．若再作一个格点正方形，并涂上阴影，使这两个格点正方形无重叠面积，且组成的图形是轴对称图形，又是中心对称图形，则这个格点正方形的作法共有（ ）
A.2种 B.3种 C.4种 D.5种
二、填空题
已知点P（﹣2，3）关于原点的对称点为M（a，b），则a+b= ．
在平面直角坐标系中，若点P(x－2，x)关于原点的对称点在第四象限，则x的取值范围是________．
如图，△DEF是由△ABC绕着某个定点旋转得到的，则这个旋转中心的坐标是______________.
如图，是4×4的正方形网格，把其中一个标有数字的白色小正方形涂黑，就可以使图中的黑色部分构成一个中心对称图形，则这个白色小正方形内的数字是 ．
三、作图题
画出四边形ABCD关于点O对称的图形．
四、解答题
(1)指出下列旋转对称图形的最小旋转角，并在图中标明它的旋转中心O.
(2)在上述几个图形中有没有中心对称图形？具体指明是哪几个？
解：图形A的最小旋转角是 度，它 中心对称图形.
图形B的最小旋转角是 度，它 中心对称图形.
图形C的最小旋转角是 度，它 中心对称图形.
图形D的最小旋转角是 度，它 中心对称图形.
图形E的最小旋转角是 度，它 中心对称图形.
如图，△ABO与△CDO关于O点中心对称，点E、F在线段AC上，且AF=CE．求证：FD=BE．
如图，△ABC中，AB=AC=2，∠BAC=45°，将△ABC绕点A按顺时针方向旋转角α得到△AEF，且0°＜α≤180°，连接BE、CF相交于点D．
（1）求证：BE=CF；
（2）当α=90°时，求四边形AEDC的面积．
\s 0 参考答案
C
C
C
答案为：B.
D
D
答案为：D；
答案为：D；
答案为：A
答案为：C．
答案为：﹣1．
答案为：0＜x＜2
答案为：（0,1）；
答案为：3．
解：如图所示：
四边形A′B′C′D′就是四边形ABCD关于点O对称的图形．
解：(1)如图所示，
(2)图形A的最小旋转角是60度，它是中心对称图形.
图形B的最小旋转角是72度，它不是中心对称图形.
图形C的最小旋转角是72度，它不是中心对称图形.
图形D的最小旋转角是120度，它不是中心对称图形.
图形E的最小旋转角是90度，它是中心对称图形.
故答案为：60，是；72，不是；72，不是；120，不是；90，是.
证明：∵△ABO与△CDO关于O点中心对称，
∴OB=OD，OA=OC.
∵AF=CE，∴OF=OE.
∵在△DOF和△BOE中， SKIPIF 1 < 0 \* MERGEFORMAT
∴△DOF≌△BOE（SAS）.
∴FD=BE．