数学第二十三章 旋转23.2 中心对称23.2.1 中心对称优秀课后复习题

这是一份数学第二十三章 旋转23.2 中心对称23.2.1 中心对称优秀课后复习题，共9页。试卷主要包含了2 中心对称》同步精炼等内容，欢迎下载使用。

一、选择题
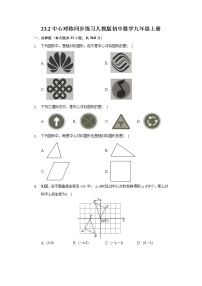
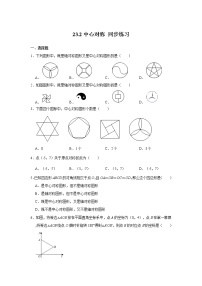
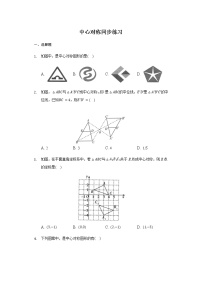
1.下列图形中，既是轴对称图形又是中心对称图形的是( )
2.如图，△ABC与△A′B′C′成中心对称，则下列说法不正确的是（ ）
A．S△ACB=S△A′B′C′
B．AB=A′B′
C．AB∥A′B′，A′C′∥AC，BC∥B′C′
D．S△A′B′O=S△ACO
3.在下列几何图形中：
(1)两条互相平分的线段；
(2)两条互相垂直的直线；
(3)两个有公共顶点的角；
(4)两个有一条公共边的正方形.
其中是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
4.如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是( )
A.点A与点A′是对称点 B.BO=B′O
C.AB∥A′B′ D.∠ACB=∠C′A′B′
5.点P(2a+1，4)与P′(1，3b﹣1)关于原点对称，则2a+b=( )
A.﹣3 B.﹣2 C.3 D.2
6.如图，在直角坐标系中，已知菱形OABC的顶点A(1，2)，B(3，3)．作菱形OABC关于y轴的对称图形OA'B'C'，再作图形OA'B'C'关于点O的中心对称图形OA″B″C″，则点C的对应点C″的坐标是( )
A．(2，﹣1) B．(1，﹣2) C．(﹣2，1) D．(﹣2，﹣1)
7.在直角坐标系中，点A的坐标为(﹣3，4)，那么下列说法正确的是( )
A.点A与点B(﹣3，﹣4)关于y轴对称
B.点A与点C(3，﹣4)关于x轴对称
C.点A与点C(4，﹣3)关于原点对称
D.点A与点F(﹣4，3)关于第二象限的平分线对称
8.点A(4，3)经过某种图形变化后得到点B(﹣3，4)，这种图形变化可以是( )
A.关于x轴对称 B.关于y轴对称
C.绕原点逆时针旋转90° D.绕原点顺时针旋转90°
9.如图，在平面直角坐标系中将△ABC绕点C(0，﹣1)旋转180°得到△A1B1C1，设点A1的坐标为(m，n)，则点A的坐标为( )
A.(﹣m，﹣n) B.(﹣m，﹣n﹣2) C.(﹣m，﹣n﹣1) D.(﹣m，﹣n＋1)
10.如图，在平面直角坐标系中Rt△ABC的斜边BC在x轴上，点B坐标为(1，0)，AC=2，∠ABC=30°，把Rt△ABC先绕B点顺时针旋转180°，然后再向下平移2个单位，则A点的对应点A′的坐标为( )
A.(﹣4，﹣2﹣eq \r(3)) B.(﹣4，﹣2+eq \r(3)) C.(﹣2，﹣2+eq \r(3)) D.(﹣2，﹣2﹣eq \r(3))
二、填空题
11.如图，是4×4的正方形网格，把其中一个标有数字的白色小正方形涂黑，就可以使图中的黑色部分构成一个中心对称图形，则这个白色小正方形内的数字是 ．
12.如图2310所示的美丽图案中，既是轴对称图形又是中心对称图形的有________个．
13.已知点A（2，4）与点B（b﹣1，2a）关于原点对称，则a= ，b= ．
14.已知点A(m2＋1，n2﹣2)与点B(2m，4n＋6)关于原点对称，则A关于x轴的对称点的坐标为_____，B关于y轴的对称点的坐标为______．
15.在平面直角坐标系中，点M(a+1,2),N(-3,b-1)关于原点对称，则ab=_____.
16.将七个边长都为1的正方形如图所示摆放，点A1、A2、A3、A4、A5、A6分别是六个正方形的中心，则这七个正方形重叠形成的重叠部分的面积是 ．
三、作图题
17.如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A(﹣2，2)，B(0，5)，C(0，2).
(1)将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形.
(2)平移△ABC，使点A的对应点A2坐标为(﹣2，﹣6)，请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标.
四、解答题
18.如图，△ABO与△CDO关于O点中心对称，点E、F在线段AC上，且AF=CE．求证：FD=BE．
19.如图，D是△ABC边BC的中点，连接AD并延长到点E，使DE=AD，连接BE．
(1)图中哪两个图形成中心对称？
(2)若△ADC的面积为4，求△ABE的面积．
20.如图①，已知△ABC与△ADE关于点A成中心对称，∠B=50°，△ABC的面积为24，BC边上的高为5，若将△ADE向下折叠，如图②点D落在BC的G点处，点E落在CB的延长线的H点处，且BH=4，则∠BAG是多少度，△ABG的面积是多少．
21.如图所示，在平面直角坐标系中，△PQR是由△ABC经过某种变换后得到的图形.
⑴仔细观察点A和点P，点B和点Q，点C和点R的坐标之间的关系，在这种变换下分别写出这六个点的坐标，从中你发现什么特征？请你用文字语言将你发现的特征表达出来；
⑵若△ABC内有一点M(2a+5,-1-3b)经过变换后，在△PRQ内的坐标为（-3，-2），根据你发现的特征，求关于x的方程2-ax=bx-3的解.
22.如图，将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置，AB与A1C1相交于点D，AC与A1C1，BC1分别交于点E，F.
(1)求证：△BCF≌△BA1D；
(2)当∠C=α度时，判定四边形A1BCE的形状，并说明理由.
答案
1.D；
2.D
3.C
4.D
5.A
6.A
7.D
8.C.
9.B
10.D
11.答案为：3．
12.答案为：3
13.答案为；﹣2，﹣1．
14.答案为：(2，﹣2)，(2，﹣2)．
15.答案为：0.5；
16.答案为：1.5；
17.解：(1)如图所示：△A1B1C即为所求；
(2)如图所示：△A2B2C2即为所求；
(3)旋转中心坐标(0，﹣2).
18.证明：∵△ABO与△CDO关于O点中心对称，
∴OB=OD，OA=OC.
∵AF=CE，∴OF=OE.
∵在△DOF和△BOE中， SKIPIF 1 < 0 \* MERGEFORMAT
∴△DOF≌△BOE（SAS）.
∴FD=BE．
19.解：(1)图中△ADC和三角形EDB成中心对称；
(2)∵△ADC和三角形EDB成中心对称，△ADC的面积为4，
∴△EDB的面积也为4，
∵D为BC的中点，
∴△ABD的面积也为4，
所以△ABE的面积为8．
20.解：依题意有AD=AB=AG，AE=AH=AC．
又∠B=50°，则∠BAG=180°-50°×2=80°；
作AD⊥BC于D，根据三角形的面积公式得到BC=9.6．
根据等腰三角形的三线合一，
可以证明CG=BH=4，则BG=5.6．
根据三角形的面积公式得△ABG的面积是14．
21.解：⑴A(4,3),B(3,1),C(1,2),P(-4,-3),Q(-3,-1),R(-1,-2),
△ABC所在平面上各点与△PQR所在平面的对应点关于原点对称.
⑵由⑴得
∴2+x=-x-3,解得x=-2.5
所以关于x的方程2-ax=bx-3的解为x=-2.5.
22.解：(1)∵△ABC是等腰三角形，∴AB=BC，∠A=∠C，
∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置，
∴A1B=AB=BC，∠A=∠A1=∠C，∠A1BD=∠CBC1，
由ASA可证△BCF≌△BA1D
(2)四边形A1BCE是菱形，理由如下：
∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1BC1的位置，
∴∠A1=∠A，
∵∠ADE=∠A1DB，
∴∠AED=∠A1BD=α，
∵∠C=α，
∴∠AED=∠C，
∴A1E∥BC，
由(1)知△BCF≌△BA1D，
∴∠C=∠A1，
∴∠A1=∠AED=α，
∴A1B∥AC，
∴四边形A1BCE是平行四边形，
又∵A1B=BC，
∴四边形A1BCE是菱形