




人教版九年级上册23.2.1 中心对称练习题
展开第二十三章 旋转
中心对称
考点1 中心对称
(1)中心对称的定义
把一个图形绕着某个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点..
(2)中心对称的性质
①关于中心对称的两个图形能够完全重合;
②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
考点2 中心对称图形
(1)定义
把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
注意:中心对称图形和中心对称不同,中心对称是两个图形之间的关系,而中心对称图形是指一个图形自身的特点,这点应注意区分,它们性质相同,应用方法相同.
(2)常见的中心对称图形
平行四边形、圆形、正方形、长方形等等.
考点3 关于原点对称的点的坐标
关于原点对称的点的坐标特点
(1)两个点关于原点对称时,它们的坐标符号相反,即点P(x,y)关于原点O的对称点是P′(﹣x,﹣y).
(2)关于原点对称的点或图形属于中心对称,它是中心对称在平面直角坐标系中的应用,它具有中心对称的所有性质.但它主要是用坐标变化确定图形.
注意:运用时要熟练掌握,可以不用图画和结合坐标系,只根据符号变化直接写出对应点的坐标.
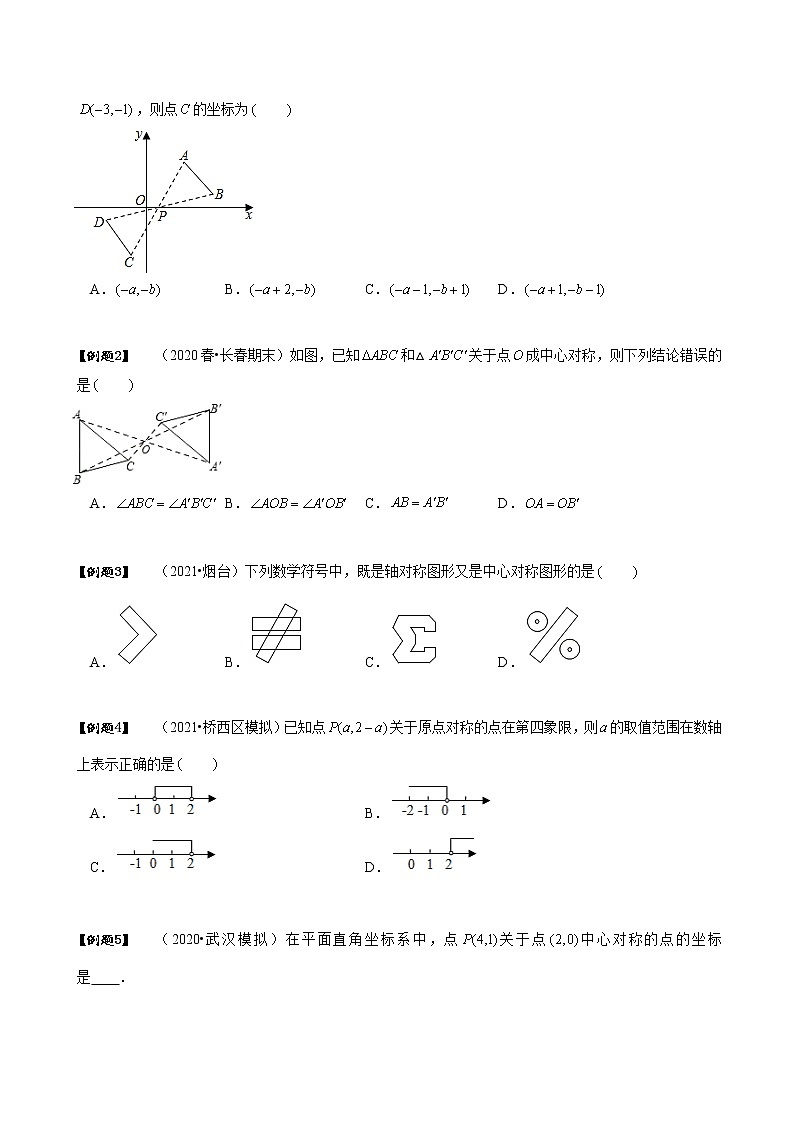
【例题1】 (2021春•南京期中)如图,线段与线段关于点对称,若点、、,则点的坐标为
A. B. C. D.
【例题2】 (2020春•长春期末)如图,已知和△关于点成中心对称,则下列结论错误的是
A. B. C. D.
【例题3】 (2021•烟台)下列数学符号中,既是轴对称图形又是中心对称图形的是
A. B. C. D.
【例题4】 (2021•桥西区模拟)已知点关于原点对称的点在第四象限,则的取值范围在数轴上表示正确的是
A. B.
C. D.
【例题5】 (2020•武汉模拟)在平面直角坐标系中,点关于点中心对称的点的坐标是 .
- (2020秋•台前县期中)将绕原点旋转得到△,设点的坐标为,则点的坐标为
A. B. C. D.
- (2021•罗湖区校级模拟)下列图形中,是轴对称图形,并且是中心对称图形的有
A.1个 B.2个 C.3个 D.4个
- (2021春•常州期末)下列卡通图案中,是中心对称图形的是
A.B. C. D.
- (2021春•德江县期末)下列美丽的轴对称图案,是中心对称图形的个数有
A.1个 B.2个 C.3个 D.4个
- (2021春•苏州期末)下列图形中,是中心对称图形的是
A. B. C. D.
- (2021春•姑苏区期末)下列图形中,是轴对称图形但不是中心对称图形的是
A. B.
C. D.
- (2021春•商河县期末)下列图形中,既是轴对称图形,又是中心对称图形的是
A. B. C. D.
- (2021春•崇川区校级期末)点关于原点对称的点的坐标为
A. B. C. D.
- (2021•淮安模拟)若点与点关于原点对称,则的值为
A. B.2 C.3 D.5
- (2021•龙岩模拟)在平面直角坐标系中,点,关于原点的对称点的坐标是
A., B., C., D.,
- (2021春•盐田区校级期中)若点与点关于原点对称,则的值是
A. B. C.4 D.6
- (2021•新城区校级模拟)已知点,与点关于原点对称,则点一定在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二.填空题(共5小题)
- (2021春•海陵区校级月考)已知,点和点关于点成中心对称,则的值为 .
- (2021春•秦淮区月考)如图,和关于点成中心对称,若,,,则的长是 .
- (2019秋•颍州区期末)如图,与△关于点成中心对称,则下列结论不成立的是
A.点与点是对称点 B.
C. D.
- (2020春•青州市期末)如图,将绕点旋转得到△,设点的坐标为,则点的坐标为
A. B. C. D.
- (2020•淮安)在平面直角坐标系中,点关于原点对称的点的坐标是
A. B. C. D.
- (2019•贵港)若点与点关于原点成中心对称,则的值是
A.1 B.3 C.5 D.7
- (2019•常德)点关于原点的对称点坐标是
A. B. C. D.
- (2019•安顺)在平面直角坐标系中,点关于原点的对称点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
- (2019•巴中)在平面直角坐标系中,已知点与点关于原点对称,则点的坐标为
A. B. C. D.
- (2019•滨州)已知点关于原点对称的点在第四象限,则的取值范围在数轴上表示正确的是
A. B.
C. D.
- (2018•成都)在平面直角坐标系中,点关于原点对称的点的坐标是
A. B. C. D.
- (2020•广安)在平面直角坐标系中,点与点关于原点对称,则 .
- (2019•阿坝州)在平面直角坐标系中,点关于原点中心对称的点的坐标为 .
人教版九年级上册23.2.1 中心对称优秀测试题: 这是一份人教版九年级上册23.2.1 中心对称优秀测试题,文件包含重难点讲义人教版数学九年级上册-提高练232中心对称原卷版docx、重难点讲义人教版数学九年级上册-基础练232中心对称原卷版docx、重难点讲义人教版数学九年级上册-知识点232中心对称原卷版docx、重难点讲义人教版数学九年级上册-提高练232中心对称解析版docx、重难点讲义人教版数学九年级上册-基础练232中心对称解析版docx、重难点讲义人教版数学九年级上册-知识点232中心对称解析版docx等6份试卷配套教学资源,其中试卷共90页, 欢迎下载使用。
初中数学23.2.1 中心对称优秀课堂检测: 这是一份初中数学23.2.1 中心对称优秀课堂检测,文件包含专题232中心对称讲练-2022-2023九年级上册同步讲练解析版人教版docx、专题232中心对称讲练-2022-2023九年级上册同步讲练原卷版人教版docx等2份试卷配套教学资源,其中试卷共34页, 欢迎下载使用。
数学九年级上册23.2.1 中心对称优秀复习练习题: 这是一份数学九年级上册23.2.1 中心对称优秀复习练习题,文件包含专题232中心对称测试卷-2022-2023九年级上册同步讲练解析版人教版docx、专题232中心对称测试卷-2022-2023九年级上册同步讲练原卷版人教版docx、专题232中心对称测试卷-2022-2023九年级上册同步讲练答题卡人教版docx等3份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。













