数学八年级下册16.1 二次根式精品课件ppt

这是一份数学八年级下册16.1 二次根式精品课件ppt，共60页。PPT课件主要包含了学习目标，知识回顾，典型例题和及时反馈，二次根式，二次根式的意义，二次根式的性质，反思提升，二次根式的运算，典型例题，及时反馈等内容，欢迎下载使用。

1、能够比较熟练地应用二次根式的性质进行化简.2、能够比较熟练地进行二次根式的运算.3、会运用二次根式的性质及运算解决简单的实际 问题.
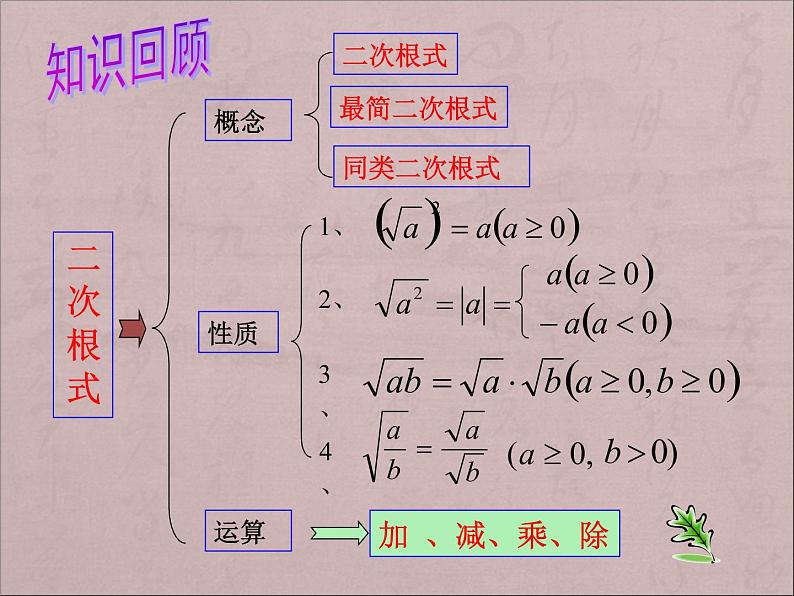
你能说说对二次根式 的认识吗?
2.a可以是数,也可以是式.
3.形式上含有二次根号.
1.表示a的算术平方根.
注:正确理解和运用二次根式的概念是学好本章的关键之一.
例1、下列各式中哪些是二次根式？哪 些不是？ 为什么？
思路启迪: 二次根式应同时具备下列三个条件：(1)含有根号；(2)根指数是2；(3)被开方数是非负数.
例2、x取何值时,下列二次根式有意义?
思路启迪：判断二次根式是否有意义的基本 依据是:①被开方数为非负数；②分母不等于零。
例3、二次根式的非负性的应用.
2、已知x,y为实数,且 +3(y-2)2 =0, 则x-y的值为( 　 ) A.3 B.-3 C.1 D.-1
解：由题意，得 x-4=0 且 2x+y=0
解得 x=4,y=-8
x-y=4-(-8)= 4+ 8 =12
解：∵x-1=0 且 y-2=0 ；∴ x=1 y=2
点评：初中阶段，课本中出现的三种非负数已全部学完．这三种非负数是：实数的绝对值；实数的偶次方；非负数的算术平方根．利用非负数的意义求值，是解决代数式求值问题时常用的方法之一．
x为何值时，下列各式在实数范围内有意义.
3、积的算术平方根的性质
4、商的算术平方根的性质
注：正确理解和运用二次根式的性质是学好本章的关键之一.
例2、把下列各式写成平方差的形式， 再在实数范围内分解因式；
化简形如 的二次根式，首先把 写成|a|的形式，再根据已知条件中字母a 的取值范围，确定其结果.
化简形如 的二次根式的方法:
一定要注意a的取值范围
例5、判断下列各式中哪些是最简二次根式，哪些不是？为什么？(字母为正数)
思路启迪：根据最简二次根式的条件来判断，不满足其中任意一个条件的，都不是最简二次根式．
最简二次根式的三个条件：（1）被开方数中不含能开得尽方的因数或 因式；（2）被开方数不含分母；（3）分母中不含有根号.
例6、化简(字母为正数)
思路启迪：若被开方数是积的形式，把能开得尽的方的因数或因式开出来；若被开方数不是积的形式，应先化成积的形式，再把可以开得尽方的因数或因式开出来．
思路启迪：化去根号中的分母，可以将被开方数的分子和分母同乘以一个适当的数(或代数式)，从而使被开方数中的分母能够开的尽,这样也就将二次根式进行化简了.
思路启迪：化去分母中的根号的关键是选择一个适当的数(或代数式)，用这个数(或代数式)去乘分式的分子和分母，可以使分母不含根号．这个数(或代数式)叫有理化因式。分母的有理化因式不是唯一的，应学会选择最简单的.
思路启迪：根据本题的特点，将分子分解因式，然后约分，这样化简运算简便．
化二次根式为最简二次根式的一般步骤：(1)把根号内能开得尽方的因数(或因式)移到根号外；(2)化去根号内的分母．(3)化去分母中的根号．(又称分母有理化)
2、把下列二次根化为最简二次根式.
4、若aA. a+b B. a-b C. -a-b D. -a+b
3、实数 在数轴上的位置如图所示,化简:
5、实数 在数轴上的位置如图所示,化简:
1、二次根式的乘法法则
2、二次根式的除法法则
二次根式的除法可以先转化为乘法,然后再按乘法法则进行运算.
三、二次根式的运算（乘除）
例1：计算(字母为正数)
点评：也可以用“除以一个数，等于乘以这个数的倒数”的法则进行计算．
在进行二次根式的加减运算时，首先要正确识别同类二次根式，关键是准确地化成最简二次根式，然后观察被开方数是否相同，对于被开方数相同的最简二次根式可以类似合并同类项的方法，即把根号外的因式相加减，根指数和被开方数都不变。
几个二次根式化成最简二次根式以后，如果被开方数相同，这几个二次根式就叫做同类二次根式.
三、二次根式的运算（加减）
例、计算(字母为正数)
例、计算(字母为正数)
点评：在进行二次根式的加减运算时，应注意：1、根号外的系数因式需保留假分数的形式。2、化简后，被开方数不相同的二次根式不能合并；反之，能合并，若合并后的系数为多项式，需添括号。
1、混合运算的顺序： 二次根式的混合运算顺序与实数运算类似，先算乘方，再算乘除，最后算加减，有括号先算括号里面的．
2、对于二次根式混合运算，原来学过的所有运算律、运算法则及乘法公式仍然适用．
三、二次根式的运算（混合运算）
点评：当被除式与除式的被开方数恰好能整除时，这样计算很方便．
一样的类型，不一样的解法，应学会选择。
点评：有关二次根式的除法，通常是先写成分式的形式，然后通过化去分母中的根号进行运算．
二次根式的混合运算，要注意：1、运算顺序； 2、灵活运用运算法则；3、灵活运用运算律和乘法公式简便运算；4、结果一定要化到最简。
在二次根式混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
思路启迪：要将根号外的因式移入根号内，根据 移入根号里面的必须是非负数，可以将 a-1写成-(1-a)，将1-a平方后移入根号内，“－”仍留在根号外面．
思路启迪：由于本题中没有指明字母的取值范围，从题中可以看出字母的取值是任意的，在去掉根号时需要进行讨论。
若a为底,b为腰,此时底边上的高为
(2)若满足上式的a,b为等腰三角形的两边,求这个等腰三角形的面积.
解:若a为腰,b为底,此时底边上的高为
点评： 题目没有直接给出a和b的取值范围，但它隐含在条件中，不易发现．所以在化简二次根式时，挖掘隐含在题目中的条件是关键．