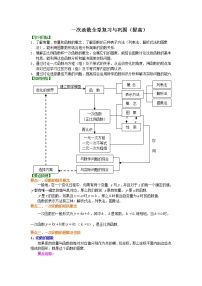
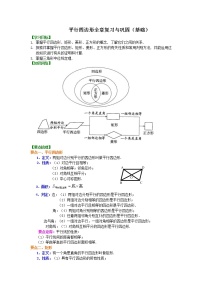
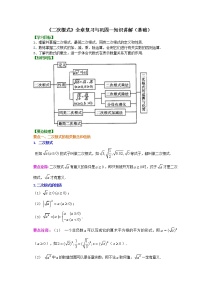
- 一次函数的应用(提高)知识讲解 教案 13 次下载
- 一次函数的应用(提高)巩固练习 试卷 16 次下载
- 一次函数全章复习与巩固(基础)巩固练习 试卷 17 次下载
- 一次函数全章复习与巩固(提高)知识讲解 教案 12 次下载
- 一次函数全章复习与巩固(提高)巩固练习 试卷 18 次下载
人教版八年级下册19.2.2 一次函数教学设计
展开【学习目标】
1.了解常量、变量和函数的概念,了解函数的三种表示方法(列表法、解析式法和图象法),能利用图象数形结合地分析简单的函数关系.
2.理解正比例函数和一次函数的概念,会画它们的图象,能结合图象讨论这些函数的基本性质,能利用这些函数分析和解决简单实际问题.
3.通过讨论一次函数与方程(组)及不等式的关系,从运动变化的角度,用函数的观点加深对已经学习过的方程(组)及不等式等内容的再认识.
4. 通过讨论选择最佳方案的问题,提高综合运用所学函数知识分析和解决实际问题的能力.
【知识网络】
变化的世界
函 数
建立数学模型
应
用
概 念
选择方案
概 念
再认识
表示方法
图 象
性 质
一次函数
(正比例函数)
一元一次方程
一元一次不等式
二元一次方程组
与数学问题的综合
与实际问题的综合
列表法
解析法
图象法
【要点梳理】
要点一、函数的相关概念
一般地,在一个变化过程中. 如果有两个变量 与,并且对于的每一个确定的值,都有唯一确定的值与其对应,那么我们就说 是自变量,是的函数.
是的函数,如果当=时=,那么叫做当自变量为时的函数值.
函数的表示方法有三种:解析式法,列表法,图象法.
要点二、一次函数的相关概念
一次函数的一般形式为,其中、是常数,≠0.特别地,当=0时,一次函数即(≠0),是正比例函数.
要点三、一次函数的图象及性质
1、函数的图象
如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
要点诠释:
直线可以看作由直线平移||个单位长度而得到(当>0时,向上平移;当<0时,向下平移).说明通过平移,函数与函数的图象之间可以相互转化.
2、一次函数性质及图象特征
掌握一次函数的图象及性质(对比正比例函数的图象和性质)
要点诠释:
理解、对一次函数的图象和性质的影响:
(1)决定直线从左向右的趋势(及倾斜角的大小——倾斜程度),决定它与轴交点的位置,、一起决定直线经过的象限.
(2)两条直线:和:的位置关系可由其系数确定:
与相交;
,且与平行;
,且与重合;
(3)直线与一次函数图象的联系与区别
一次函数的图象是一条直线;特殊的直线、直线不是一次函数的图象.
要点四、用函数的观点看方程、方程组、不等式
【典型例题】
类型一、函数的概念
1、下列说法正确的是:( )
A.变量满足,则是的函数;
B.变量满足,则是的函数;
C.变量满足,则是的函数;
D.变量满足,则是的函数.
【答案】A;
【解析】B、C、D三个选项,对于一个确定的的值,都有两个值和它对应,不满足单值对应的条件,所以不是函数.
【总结升华】理解函数的概念,关键是函数与自变量之间是单值对应关系,自变量的值确定后,函数值是唯一确定的.
举一反三:
【变式】如图的四个图象中,不表示某一函数图象的是( )
【答案】B;
2、求函数的自变量的取值范围.
【思路点拨】要使函数有意义,需或解这个不等式组即可.
【答案与解析】
解:要使函数有意义,则要符合:
即:或
解方程组得自变量取值是或.
【总结升华】自变量的取值范围是使函数有意义的的集合.
举一反三:
【变式】求出下列函数中自变量的取值范围
(1)(2)(3)
【答案】
解:(1)要使有意义,需,解得≠0且≠-1;
(2)要使有意义,需,解得;
(3)要使有意义,需,解得.
类型二、一次函数的解析式
3、已知与成正比例关系,且其图象过点(3,3),试确定与的函数关系,并画出其图象.
【思路点拨】与成正比例关系,即,将点(3,3)代入求得函数关系式.
【答案与解析】
解:设,由于图象过点(3,3)知,故.
其图象为过点(2,0)与(0,-6)的一条直线(如图所示).
【总结升华】与成正比例满足关系式,与-2成正比例满足关系式,注意区别.
举一反三:
【变式】直线平行于直线,且与轴交于点(2,0),求这条直线的解析式.
【答案】
解:∵直线平行于直线
∴
∵与轴交于点(2,0)
∴ ①
将=2代入①,得
∴此直线解析式为.
类型三、一次函数的图象和性质
4、已知正比例函数(≠0)的函数值随的增大而减小,则一次函数的图象大致是图中的( ).
【答案】B;
【解析】∵随的增大而减小,∴ <0.
∵中的系数为1>0,<0, ∴经过一、三、四象限,故选B.
【总结升华】本题综合考查正比例函数和一次函数图象和性质,>0时,函数值随自变量的增大而增大.
举一反三:
【变式】 已知正比例函数的图象上两点A(, ), B(,),当 时, 有, 那么 的取值范围是( )
A. B. C. D.
【答案】 A;
提示:由题意随着的增大而减小,所以,选A答案.
类型四、一次函数与方程(组)、不等式
5、(2016春•鄂托克旗期末)如图,直线y=﹣2x 与直线y=kx+b 相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0)
(1)求直线y=kx+b的解析式.
(2)求两条直线与y轴围成的三角形面积.
(3)直接写出不等式(k+2)x+b≥0的解集.
【思路点拨】(1)首先确定点A的坐标,然后利用点B的坐标利用待定系数法确定直线的解析式即可;
(2)首先根据直线AB的解析式确定直线AB与y轴的交点坐标,从而利用三角形的面积公式求得三角形的面积;
(3)将不等式变形后结合函数的图象确定不等式的解集即可.
【答案与解析】
解:(1)把A(a,2)代入y=﹣2x中,得﹣2a=2,
∴a=﹣1,
∴A(﹣1,2)
把A(﹣1,2),B(2,0)代入y=kx+b中得,
∴k=﹣,b=,
∴一次函数的解析式是y=﹣x+;
(2)设直线AB与Y轴交于点C,则C(0,)
∴S△BOC=××1=;
(3)不等式(k+2)x+b≥0可以变形为kx+b≥﹣2x,
结合图象得到解集为:x≥﹣1.
【总结升华】本题考查了一次函数与一元一次不等式的知识,解题的关键是能够根据题意确定直线的解析式,然后结合图象直接写出不等式的解集.
举一反三:
【变式】(2015•武汉校级模拟)已知一次函数y=kx+b的图象经过点(3,5)与(﹣4,﹣9).
(1)求这个一次函数的解析式;
(2)求关于x的不等式kx+b≤5的解集.
【答案】解:∵一次函数y=kx+b的图象经过点点(3,5)与(﹣4,﹣9),
∴,
解得
∴函数解析式为:y=2x﹣1;
(2)∵k=2>0,
∴y随x的增大而增大,
把y=5代入y=2x﹣1解得,x=3,
∴当x≤3时,函数y≤5,
故不等式kx+b≤5的解集为x≤3.
类型五、一次函数的应用
6、(2015•黔西南州)某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过12吨(含12吨)时,每吨按政府补贴优惠价收费;每月超过12吨,超过部分每吨按市场调节价收费,小黄家1月份用水24吨,交水费42元.2月份用水20吨,交水费32元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少元;
(2)设每月用水量为x吨,应交水费为y元,写出y与x之间的函数关系式;
(3)小黄家3月份用水26吨,他家应交水费多少元?
【答案与解析】
解:(1)设每吨水的政府补贴优惠价为a元,市场调节价为b元.
根据题意得,
解得:.
答:每吨水的政府补贴优惠价为1元,市场调节价为2.5元.
(2)∵当0≤x≤12时,y=x;
当x>12时,y=12+(x﹣12)×2.5=2.5x﹣18,
∴所求函数关系式为:y=.
(3)∵x=26>12,
∴把x=26代入y=2.5x﹣18,得:y=2.5×26﹣18=47(元).
答:小英家三月份应交水费47元.
【总结升华】本题考查了一次函数的应用,题目还考查了二元一次方程组的解法,特别是在求一次函数的解析式时,此函数是一个分段函数,同时应注意自变量的取值范围.
举一反三:
【变式】一报刊销售亭从报社订购某晚报的价格是每份0.7元,销售价是每份1元,卖不掉的报纸还可以以0.20元的价格返回报社,在一个月内(以30天计算),有20天每天可卖出100份,其余10天,每天可卖出60份,但每天报亭从报社订购的份数必须相同,若以报亭每天从报社订购报纸的份数为,每月所获得的利润为.
(1)写出与之间的函数关系式,并指出自变量的取值范围;
(2)报亭应该每天从报社订购多少份报纸,才能使每月获得的利润最大?最大利润是多少?
【答案】
解:(1)
.
类型六、一次函数综合
7、如图所示,直线的解析表达式为,且与轴交于点D,直线经过A、B两点,直线、交于点C.
(1)求点D的坐标;
(2)求直线的解析表达式;
(3)求△ADC的面积;
(4)在直线上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
【答案与解析】
解: (1)由,当=0,得=0,得=l.∴ D(1,0).
(2)设直线的解析表达式为,
由图象知,,;,.
将这两组值代入,得方程组
解得
∴ 直线的解析表达式为.
(3)∵ 点C是直线与的交点,于是有
解得 ∴ C(2,-3).
∴ △ADC的AD边上的高为3.
∵ OD=1,OA=4,
∴ AD=3.
∴ .
(4)P(6,3).
【总结升华】这是一道一次函数图象与性质的综合应用问题,求直线的函数解析式,一般运用待定系数法,但运用过程中,又要具体问题具体分析;求底边在坐标轴上三角形的面积的关键是探求该三角形的高.方程(组)、不等式问题
函 数 问 题
从“数”的角度看
从“形”的角度看
求关于、的一元一次方程=0(≠0)的解
为何值时,函数的值为0?
确定直线与轴(即直线=0)交点的横坐标
求关于、的二元一次方程组的解.
为何值时,函数与函数的值相等?
确定直线与直线的交点的坐标
求关于的一元一次不等式>0(≠0)的解集
为何值时,函数的值大于0?
确定直线在轴(即直线=0)上方部分的所有点的横坐标的范围
专题 19.48 《一次函数》全章复习与巩固(知识讲解)-八年级数学下册基础知识专项讲练(人教版): 这是一份专题 19.48 《一次函数》全章复习与巩固(知识讲解)-八年级数学下册基础知识专项讲练(人教版),共22页。教案主要包含了学习目标,知识网络,要点梳理,典型例题等内容,欢迎下载使用。
人教版九年级上册第二十四章 圆综合与测试精品教案: 这是一份人教版九年级上册第二十四章 圆综合与测试精品教案,共12页。教案主要包含了学习目标,知识网络,要点梳理,典型例题,答案与解析等内容,欢迎下载使用。
人教版九年级上册第二十四章 圆综合与测试公开课教学设计: 这是一份人教版九年级上册第二十四章 圆综合与测试公开课教学设计,共10页。教案主要包含了学习目标,知识网络,要点梳理,典型例题,总结升华,答案与解析等内容,欢迎下载使用。