初中数学21.1 二次根式优秀ppt课件

这是一份初中数学21.1 二次根式优秀ppt课件，共19页。PPT课件主要包含了学习目标，的算术平方根是0，观察与思考，导入新课，下球体，b-3，讲授新课，二次根式的定义，知识归纳，m≤0等内容，欢迎下载使用。

1.理解二次根式的概念;
2.会确定二次根式有意义时字母的取值范围; (重点)
3.探索二次根式的性质; (难点)
4.运用二次根式的性质进行化简计算. (难点)
问题2 什么是一个数的算术平方根？如何表示？
正数的正的平方根叫做它的算术平方根.
问题1 什么叫做一个数的平方根？如何表示？
一般地，若一个数的平方等于a，则这个数就叫做a的平方根.
正数有两个平方根且互为相反数；0有一个平方根就是0；负数没有平方根.
问题3 平方根的性质：
问题4 所有实数都有算术平方根吗？
正数和0都有算术平方根；负数没有算术平方根.
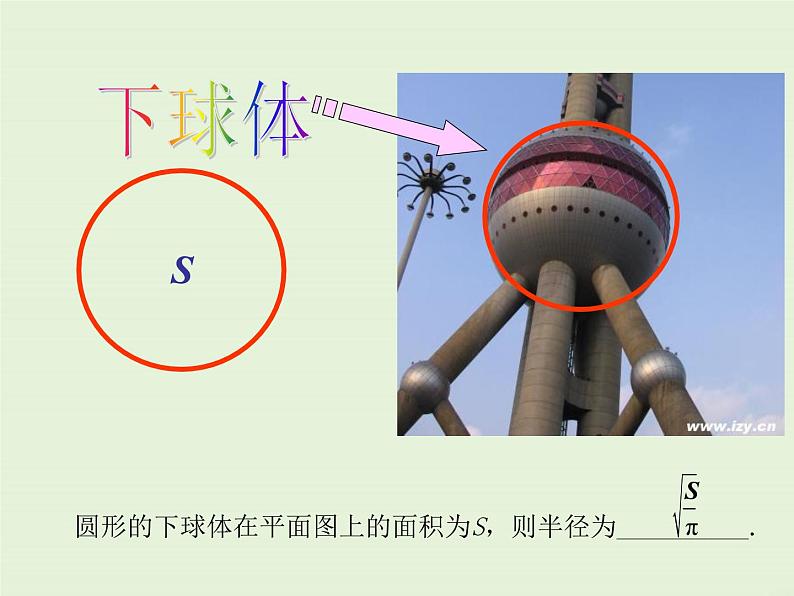
圆形的下球体在平面图上的面积为S，则半径为__________.
如图所示的值表示正方形的面积，则
正方形的边长是 .
表示一些正数的算术平方根．
你认为下列各代数式有哪些共同特点？
2.二次根式实质上是非负数的算术平方根.
3. a既可以是一个数，也可以是一个式子.
1. 既可表示开方运算,也可表示运算的结果.
请你凭着自己已有的知识,说说对二次根式 的认识！
例 下列各式是二次根式吗?
（1）、（4）、（6）均是二次根式，其中 +1属于“非负数+正数”的形式一定大于零.而（5）中xy<0,（7）根指数不是2，是3.而（3）不是，是因为在实数范围内，负数没有平方根.
1.根据算术平方根的意义填空，并说出得到结论的依据．
由其定义我们还可进一步知道：二次根式具有双重非负性.到目前为止，非负数的三种表现形式归纳如下：a2, ︱a︱,文字叙述：任何一个非负数算术平方根的平方都等于这个数.
（2）用到了（ab）2=a2b2这个结论.
2.从取值范围来看,
思考：当x是怎样的实数时， 在实数范围内有意义？
2.（1）若 , 则a-b+c=___ ；
（1）由题意可知a-2=0,b-3=0,c-4=0,解得a=2,b=3,c=4.
所以a-b+c=2-3+4=3.
（2）由题意知1-x≥0,且x-1≥0,联立解得x=1.从而知y=2015,
所以x+2y=1+2×2015=4031.
（1）二次根式的概念（2）根号内字母的取值范围（3）二次根式的值
抓住被开数必须为非负数，从而建立不等式求出其解集.