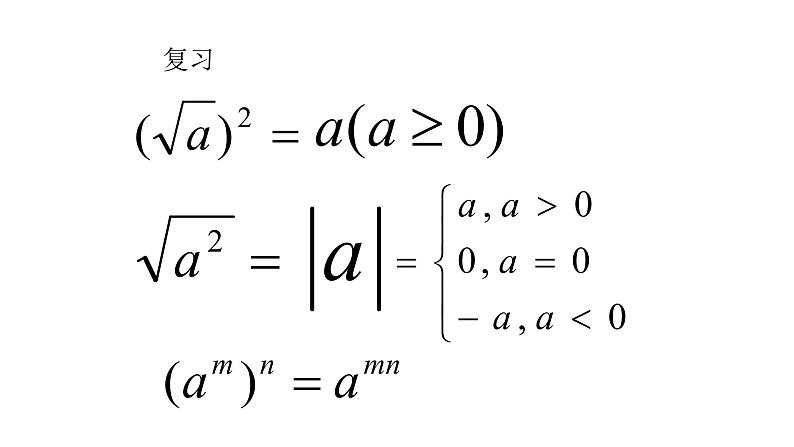
北师大版八年级上册7 二次根式示范课ppt课件

这是一份北师大版八年级上册7 二次根式示范课ppt课件，共28页。PPT课件主要包含了练习计算下列各式，故也可这样算，观察下列代数式，共同特征，探究新知，概念归纳，火眼金睛，做一做，例1化简，被开方数不含平方数等内容，欢迎下载使用。

由2，3，4发现：指数变为一半，
其实二次根式可以看作是指数为
(其中b=24，c=25)
都含有开平方运算，并且被开方数都是非负数.
上面这些式子都叫二次根式
二次根式必须具备特点：
1、根指数为2.2、被开方数必须是非负数.
请指出下列哪些是二次根式？
一、计算下列各式，你能得到什么猜想?
1、积的算术平方根等于积中各因式的算术平方根的积；
2、商的算术平方根等于被除式的算术平方根除以除式的算术平方根.
观察例1的化简结果（关键看被开方数），想一想有什么共同特征？
被开方数不含有开得尽方的因数或因式;
最简二次根式概念： 一般地，被开方数不含分母，也不含能开得尽方的因数或因式，这样的二次根式，叫做最简二次根式.
1、被开方数不含分母;2、被开方数不含能开得尽方的因数或因式;3、分母不含根号.
中是最简二次根式的有（ ）个.
以上化简过程有何规律呢？
根号里面的数有一部分移到了根号外面，具体来说是能开得尽方的因数，开方后写到了根号外面．
被开方数若有开得尽的因数，必须进行化简．
习题2.9 1，2，3，4
将公式等号的左边与右边对换
上述化简过程称为分母有理化。即把分母中的根号化去。
【例】求下列二次根式中字母的取值范围：
【解析】（1）由于被开方数是非负数，可 知a+1≥0，即a≥-1. （2）由于被开方数是非负数，且分母不 为零，可知1-2a>0，即a< . （3）由（a-3）2≥0，可知a可以取任意实数.
1.x取何值时,下列二次根式有意义?
2．下列式子一定是二次根式的是（ ）A． B． C． D．【解析】选C.A项中只有当x≤-2时，才是二次根式，故A项不一定是二次根式；B项中当x≥0时是二次根式，故B项不一定是二次根式；C项中无论x为何值，x2+2＞0，所以C项一定是二次根式；D项中当x=0时，不是二次根式，所以D项也不正确.