




初中数学人教版(2024)八年级上册14.2.1 平方差公式教学ppt课件
展开理解平方差公式,能运用公式进行计算;
经历平方差公式的探索及推导过程,掌握平方差公式的结构特征.
【探究】计算下列多项式的积,你能发现什么规律?
① ( x+1) ( x-1)② (m+2) (m-2) ③ (2x+1)(2x-1)
【发现】两个数的和与这两个数差的积,等于这两个数的平方差
你能将发现的规律用式子表示出来吗?
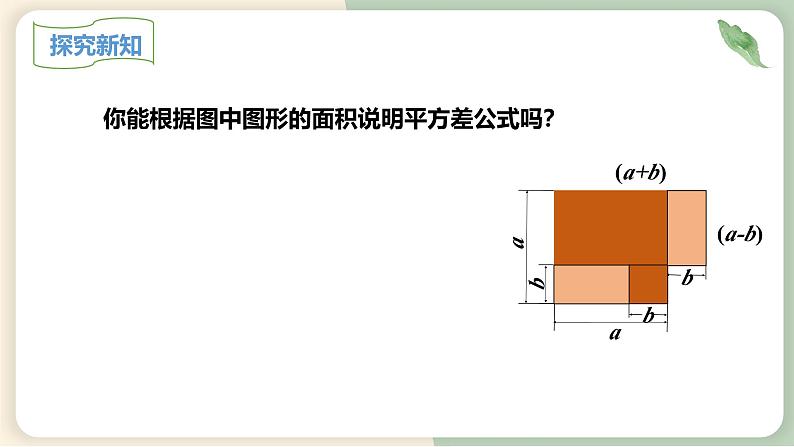
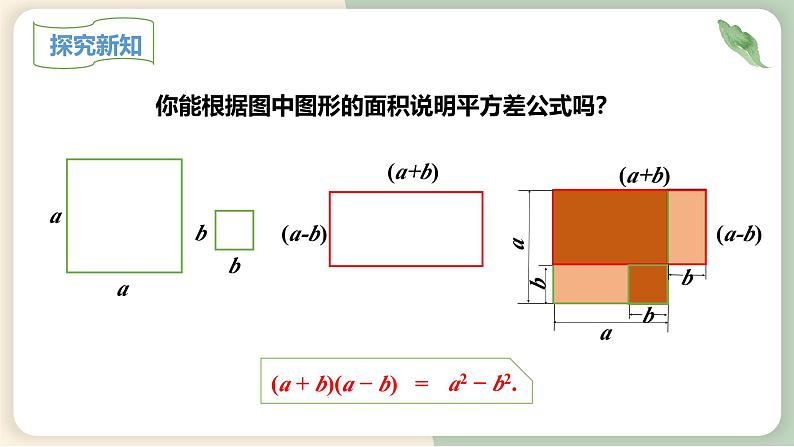
(a+b)(a-b) = a2-b2
(a + b)(a − b) =
a2 − ab + ab − b2
(a + b)(a − b) =
文字说明:两个数的___与这两个数的___的积,等于这两个数的______ .
左边:a符号相同,b符号相反.
右边:符号相同项 a 的平方减去 符号相反项 b 的平方.
a和b可以是数字、单项式或多项式等
你能根据图中图形的面积说明平方差公式吗?
(a + b)(a − b) =
(1) (3x+2)(3x-2) (2) (-x+2y)(-x-2y).
分析:在(1)中,可以把 3x 看成 a ,把 2 看成 b, 即 (3x+2)(3x-2)= ( 3x)2 - 22 (a+ b)(a - b) = a2 - b2
解:(1) (3x+2)(3x-2) = ( 3x)2 - 22 =9x2 -4
分析:在(2)中,可以把 -x 看成 a,把 2y 看成 b, 即 (-x+2y) (-x-2y) = ( -x)2 - ( 2y)2 (a+b) ( a - b) = a2 - b2
解:(2) (-x+2y)(-x-2y) = ( -x)2 - ( 2y)2 = x2 - 4y2
(1) (3x+2)(3x-2) (2) (-x+2y)(-x-2y).
(1) ( y+2)( y-2 ) - ( y-1 )( y+5 ) (2) 102×98
分析:(1)中前半部分符合平方差公式的条件,可以运用公式简化运算. 后半部分的运算仍按乘法法则进行.
解:(1) (y+2)(y-2) - (y-1)(y+5) = y2 - 22 - ( y2+ 4y -5) = y2 - 4 - y2- 4y +5 = - 4y +1
(1) (y+2)(y-2) - (y-1)(y+5) (2) 102×98
分析:(2) 中的102可以变形为100+2,98可以变形为100-2.然后运用平方差公式.
解:(2) 102×98 =(100+2)(100-2) =1002 - 22 =10000 - 4 =9996
应用平方差公式计算时,应注意:
(2)符号相同看作 a ,符号相反看作 b,套用公式.
中的各项,除符号外是否完全相同);
(1)观察该运算是否符合平方差公式 (两个多项式
两个数的和与这两个数的差的积,等于这两个数的平方差
数学14.2.1 平方差公式教学课件ppt: 这是一份数学<a href="/sx/tb_c88722_t3/?tag_id=26" target="_blank">14.2.1 平方差公式教学课件ppt</a>,共22页。PPT课件主要包含了给我最大快乐的等内容,欢迎下载使用。
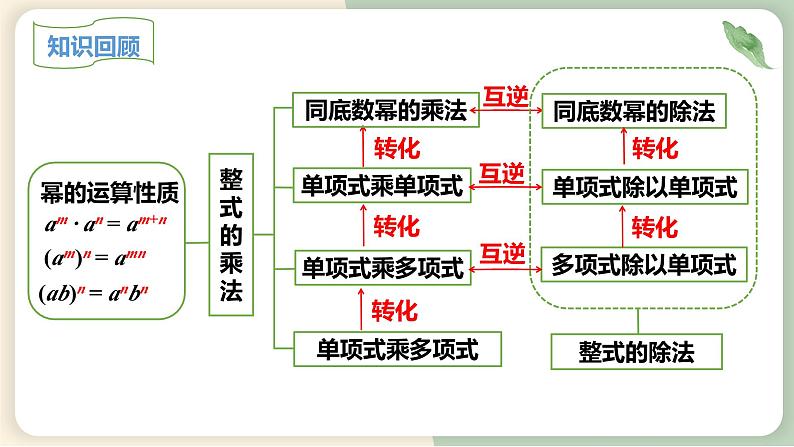
初中数学人教版八年级上册14.2.1 平方差公式教学ppt课件: 这是一份初中数学人教版八年级上册<a href="/sx/tb_c88722_t3/?tag_id=26" target="_blank">14.2.1 平方差公式教学ppt课件</a>,共24页。PPT课件主要包含了学习目标,知识回顾,整式的乘法,单项式乘单项式,单项式乘多项式,同底数幂的乘法,同底数幂的除法,单项式除以单项式,多项式除以单项式,引入新知等内容,欢迎下载使用。
初中数学人教版八年级上册第十四章 整式的乘法与因式分解14.2 乘法公式14.2.1 平方差公式集体备课课件ppt: 这是一份初中数学人教版八年级上册第十四章 整式的乘法与因式分解14.2 乘法公式14.2.1 平方差公式集体备课课件ppt,共29页。PPT课件主要包含了学习目标,新课导入,复习引入,2把各乘积相加,新知探究,x2-1,m2-4,x2-12,m2-22,2m2-12等内容,欢迎下载使用。













