人教版（2024）八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称当堂达标检测题

这是一份人教版（2024）八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称当堂达标检测题，共21页。

一、选择题：（本大题共10小题，每小题4分，共40分，给出的四个选项中，只有一项是符合题目要求的）
1.在下列四个标志中，是轴对称图形的是( )
A.B.C.D.
2.用一条长为的细绳围成一个等腰三角形，若有一边长为，则这个等腰三角形的腰长为( )
A.B.C.或D.
3.如图在和都是等边三角形，则的根据是( )
A.SSSB.SASC.ASAD.AAS
4.如图，将一个含角的直角三角板放在直角坐标系中，三角板两锐角顶点分别落在x轴，y轴上的点A，B处，直角顶点落在点处，则的值为( )
A.4B.4.5C.6D.8
5.若点与点关于y轴对称，则( )
A.1B.-1C.-2021D.2022
6.如图，在中，，分别以点A和点C为圆心，大于的长为半径作弧，两弧相交于M，N两点，作直线MN.直线MN与AB相交于点D，连接CD，若，则CD的长是( )
A.1B.1.5C.3D.6
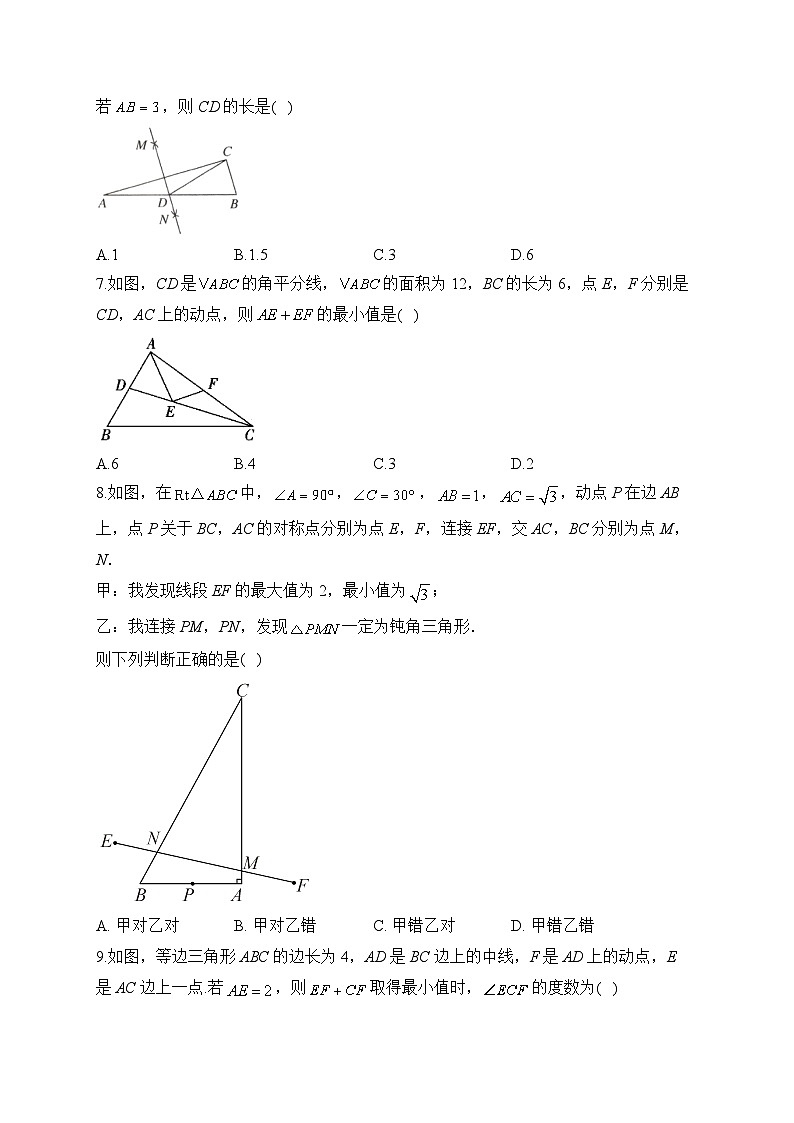
7.如图，CD是的角平分线，的面积为12，BC的长为6，点E，F分别是CD，AC上的动点，则的最小值是( )
A.6B.4C.3D.2
8.如图，在中，，，，，动点P在边AB上，点P关于BC，AC的对称点分别为点E，F，连接EF，交AC，BC分别为点M，N．
甲：我发现线段EF的最大值为2，最小值为；
乙：我连接PM，PN，发现一定为钝角三角形．
则下列判断正确的是( )
A. 甲对乙对B. 甲对乙错C. 甲错乙对D. 甲错乙错
9.如图，等边三角形ABC的边长为4，AD是BC边上的中线，F是AD上的动点，E是AC边上一点.若，则取得最小值时，的度数为( )
A.15°B.22.5°C.30°D.45°
10.如图，已知等边和等边，点P在BC的延长线上，EC的延长线交AP于点M，连接BM；下列结论：
①；
②；
③BM平分；
④，
其中正确的有( )
A.1个B.2个C.3个D.4个
二、填空题（每小题4分，共20分）
11.如图,在底边,的等腰三角形ABC中,DE垂直平分AB于点D,交BC于点E,则的周长为________.
12.如图，点O为三边垂直平分线的交点.，则_____度.
13.如图，的面积为12，，BD平分，M、N分别是BD、BC上一动点.则最小值等于___________.
14.如图，AD为等边的高，E、F分别为线段AD、AC上的动点，且，当取得最小值时，_______°.
15.如图，中，，D在BC下方且，AE平分交BD的延长线于E，连接EC，则与的数量关系式为_________.
三、解答题（本大题共6小题，共计60分，解答题应写出演算步骤或证明过程）
16.（8分）如图，A,B,C是平面内三点.
（1）按要求作图：
①作射线BC，过点B作直线l，使A,C两点在直线l两旁；
②点P为直线l上任意一点，点Q为射线BC上任意一点，连接线段AP,PQ.
（2）在（1）所作图形中，若点A到直线l的距离为2，点A到直线BC的距离为5，点A,B之间的距离为8，点A,C之间的距离为6，求的最小值，并写出其依据.
17.（8分）如图，在中，和的平分线交于点E，交AC于N，若、周长分别为和.
(1)求证：为等腰三角形；
(2)线段BC的长.
18.（10分）如图，在中，，点M，N分别在边AB，BC上，连接AN，且和关于直线MN对称.
（1）若，则的度数为______.
（2）若，，且的周长为36，求的周长.
19.（10分）小明将两个大小不同的等腰直角三角板按如图（1）所示的方式放置在同一平面内.从图（1）中抽象出一个几何图形[如图（2）]，B，C，E三点在同一条直线上，连接DC.猜想线段CD与BE之间的数量关系和位置关系，并证明你的结论.
20.（12分）如图，在平面直角坐标系中，的顶点坐标分别为、、，线段EF两端点的坐标分别为，，直线轴，交x轴于，且线段EF与CD关于y轴对称，线段CD与MN关于直线l对称.
（1）求点N、M的坐标（用含m、a的代数式表示）；
（2）与通过平移能重合吗？能与不能都要说明理由，若能，请你写出一个平移方案（平移的单位数用m、a表示）.
21.（12分）在中，，D为BC延长线上一点，点E为线段AC，CD的垂直平分线的交点，连接EA，EC，ED.
(1)如图1，当时，则________°；
(2)当时，
①如图2，连接AD，判断的形状，并证明；
②如图3，直线CF与ED交于点F，满足.P为直线CF上一动点.当的值最大时，用等式表示PE，PD与AB之间的数量关系为____________，并证明.
答案以及解析
1.答案：A
解析：A、是轴对称图形，故本选项正确；
B、不是轴对称图形，故本选项错误；
C、不是轴对称图形，故本选项错误；
D、不是轴对称图形，故本选项错误.
故选：A.
2.答案：D
解析：分两种情况讨论.①若底边长为，则腰长为；②若腰长为，则底边长为，因为，不符合三角形两边的和大于第三边，所以不能围成腰长为的等腰三角形.综上可知，这个等腰三角形的腰长为.
3.答案：B
解析：由和都是等边三角形，可得，，，进而得到，即，因此可知在和中，，，，可根据证得.
故选B
4.答案：C
解析：如图，过点C作轴于点D，轴于点E，则.点，.是等腰直角三角形，，.在和中，，，.
5.答案：A
解析：点与点关于y轴对称，
，，
解得，，
，
故选：A.
6.答案：B
解析：解：由已知可得，MN是线段AC的垂直平分线，
设AC与MN的交点为E，
，
，
，
，
，
，
，
故选：B.
7.答案：B
解析：如图，作点A关于CD的对称点H.CD是的角平分线，点H一定在BC上.过H作于F，交CD于E，此时的值最小，的最小值.过A作于G.
的面积为12，BC的长为6，，CD垂直平分AH，，，，的最小值是4，故选B.
8.答案： A
解析：连接CP，CE，CF，PM，PN，
点P关于BC，AC的对称点分别为点E，F，
，，，，
，
是等边三角形，
当点P与B重合时，CP最大为，
当点P与A重合时，CP最小为，
EF的最大值为2，最小值为，故甲正确；
由对称性知，，，
，
是钝角三角形，故乙正确，
故选：A．
9.答案：C
解析：如图,连接交于点是等边三角形的中线,,此时的值最小.是的中点.是等边三角形,平分,.,.故选C.
10.答案：D
解析：证明：①等边和等边，
，，，
在和中，
，
，故此选项正确；
②，
，
，
则，故此选项正确；
③过点B作于N，于F，
，
，
在和中，
，
，
，
BM平分，故此选项正确；
④在BM上截取，连接AK，
由②知，
，
由③知：BM平分，
，
，
又，
，
，
，
，
，
在和中
，
，
为等边三角形，则，故，故此选项正确；
故选D.
11.答案：
解析:垂直平分AB,
,
,
的周长为
故答案为:.
12.答案：60
解析：如图，连接OA，
点O是三边垂直平分线的交点，
，
，，
，
，
，
，
.
故答案为：60.
13.答案：4
解析：在AB边上取，连接，
BD平分，
，
在和中，，
，
，
，
当C、M、共线，且垂直于AB时，最小，
过点C作于E，
的面积为12，
，
，
的最小值为4，
故答案为：4.
14.答案：105
解析：如图1，过点C作，且，连接BH交AD于M，连接FH，
是等边三角形，，
，，
，
，，
，
，
，
，
，，
当F为AC与BH的交点时，如图2，的值最小，
此时，，。
故答案为：105.
15.答案：
解析：如图，设AE与BC交于点F，连接CD，与AE交于点G，连接DF.
AE平分，
.
在与中，
，
，
，，
，
，
AE垂直平分CD，
，，
，.
，
，
即，
.
，，
，
，
.
在四边形ABEC中，，
.
故答案为：.
16.答案：（1）（作法不唯一）如图所示，射线BC，直线l，线段AP,PQ即为所求.
（2）如图，
过点A作于点Q，交直线l于点P，此时的值最小.
因为点A到直线BC的距离为5，所以的最小值为5，依据是垂线段最短.
17.解析：如图所示：
(1)BE是的角平分线，
，
又，
，
，
为等腰三角形；
(2)为等腰三角形，
，
同理可得：，
又，
，
，
.
又，
.
18.解析：（1），，
，
和关于直线MN对称，
，
，
故答案为：.
（2）的周长为36，
，
，，
，解得，
.
和关于直线MN对称，
，
的周长.
19.解析：猜想：，.
证明：和均为等腰直角三角形，
，，，
，
.
在和中，
，
，.
，
，
.
20.（1）答案：见解析
解析：线段EF与CD关于y轴对称，线段EF两端点的坐标分别为，，
，.
设CD与直线l之间的距离为x，
CD与MN关于直线l对称，l与y轴之间的距离为a，
MN与y轴之间的距离为，易知，
点M的横坐标为，
，.
（2）答案：能重合.
解析：，，
轴，轴，
，
，
与通过平移能重合.
平移方案：将向上平移个单位后，再向左平移m个单位.
21.答案：(1)80
(2)①时等边三角形
②
解析：(1)如图1中，
点E是线段AC，CD的垂直平分线的交点，
，
，，
，，
，
，
，
，
故答案为：80.
(2)①结论：时等边三角形.
理由：如图2中，
点E是线段AC，CD的垂直平分线的交点，
，
，，
，，
，
，
，
，
时等边三角形；
②结论：.
理由：如图3中，作点D关于直线CF的对称点，连接，，.
当点P在的延长线上时，的值最大，此时，
，，
，
，
，
，
，
，
，
，
时等边三角形，
，，
，
，
，
，
，，
，
.
故答案为：.