



初中数学北师大版(2024)八年级上册1 探索勾股定理教课内容ppt课件
展开经历运用拼图的方法说明勾股定理是正确的过程,在数学活动中发展学生的探究意识和合作交流的习惯.掌握勾股定理和它的简单应用.
通过从实际问题中抽象出直角三角形这一模型,初步掌握转化和数形结合的思想方法.
在数学活动中发展了学生的探究意识和合作交流的习性;体会勾股定理的应用价值,增加学生应用数学知识解决实际问题的经验和感受.
经历勾股定理的验证过程,能利用勾股定理解决实际问题.
用拼图法验证勾股定理.
思考1:
勾股定理的内容是什么?
直角三角形两直角边的平方和等于斜边的平方.如果a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
思考2:
我们是通过什么方法发现了勾股定理的?
通过测量和数格子的方法
思考3:
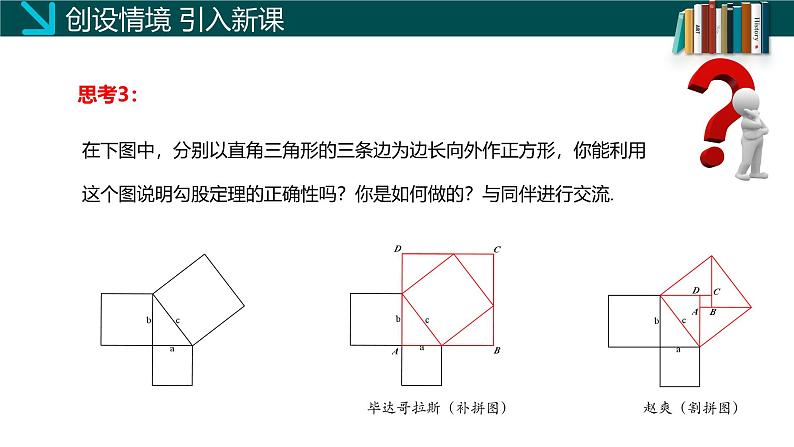
在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
正方形ABCD的面积可以表示为 ;也可以表示为 .
观察右图(毕达哥拉斯法)
a2+2ab+b2 = c2 +2ab
∴ a2+b2=c2
即:直角三角形两直角边的平方和等于斜边的平方。
c2 =2ab+b2-2ab+a2
1.常用方法:通过拼图法利用求面积来验证.这种方法是以数形转换为指导思想,图形拼补为手段,以各部分面积之间的关系为依据而达到目的的.(面积法)
2.用拼图法验证勾股定理的思路: (1)图形经过割补、拼接后,只要没有重叠,没有空隙,面积不会改变; (2)根据同一种图形的面积的不同表示方法列出等式; (3)利用等式性质验证结论成立, 即拼出图形→写出图形面积的表达式→找出等量关系→恒等变形→推导结论.
1876年,美国总统Garfield利用右图验证了勾股定理.你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系.(美国总统的证法)
青朱出入图(中国古代)
如图,过 A 点画一直线 AL 使其垂直于 DE, 并交 DE 于 L,交 BC 于 M.通过证明△BCF≌△BDA,利用三角形面积与长方形面积的关系,得到正方形ABFG与矩形BDLM等积,同理正方形ACKH与 矩形MLEC也等积,于是推得
1.用四个边长均为a,b,c的直角三角板,拼成如 图所示的图形,则下列结论中正确的是( )
A.c2=a2+b2 B.c2=a2+2ab+b2C.c2=a2-2ab+b2 D.c2=(a+b)2
2.观察下图,用数格子的方法判断图中三角形的三边长是否满足a2+b2=c2.
我方侦察员小王在距离东西向公路400m处侦察,发现一 辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
分析:根据题意,可以画出右图,其中点A表示小王所在位置,点C、点B表示两个时刻敌方汽车的位置.由于小王距离公路400m,因此∠C是直角,这样就可以由勾股定理来解决这个问题了.
解:由勾股定理,可以得到AB2=BC2+AC2, 也就是5002=BC2+4002, 所以BC=300.敌方汽车10s行驶了300m, 那么它1h行驶的距离为300×6×60=108000(m), 即它行驶的速度为108km/h.
两棵树之间的距离为8 m,两棵树的高度分别是8 m,2 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,这只小鸟至少要飞多少米?
分析:先根据题意画出图形,然后添加辅助线,构造直角三角形,再利用勾股定理求解.
解:根据题意画出示意图,如图所示, 两棵树的高度分别为AB=8 m,CD=2 m, 两棵树之间的距离BD=8 m, 过点C作CE⊥AB,垂足为E,连接AC. 则BE=CD=2 m,EC=BD=8 m, AE=AB-BE=8-2=6(m). 在Rt△ACE中,由勾股定理,得AC2=AE2+EC2, 即AC2=62+82=100,所以AC=10 m. 答:这只小鸟至少要飞10 m.
1. 《九章算术》中的“折竹抵地”问题(如图):今有竹高一丈,末折抵地,去根六尺,问折高者几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部6尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2-6=(10-x)2 B.x2-62=(10-x)2C.x2+6=(10-x)2 D.x2+62=(10-x)2
1.勾股定理是一个重要的数学定理,它将图形(直角三角形)与数量关系(三边关系)有机结合起来;在几何及日常生活中都有着广泛的应用.
3.运用勾股定理进行计算分三步:第一步:注意应用的前提,即看是不是直角三角形;第二步:分清求解的对象,即看是求直角边长,还是斜边长或者两种均有可能;第三步:运用勾股定理进行计算.
2.勾股定理的应用:(1)已知直角三角形的两边长,求其第三边长;(2)已知直角三角形的一边,确定其另两边长之间的关系;(3)证明含有平方关系的几何关系;(4)解决生产、生活中的实际问题。
转化思想,类比思想,整体思想。
勾股定理的验证:面积法;几何无字证明法。
初中数学北师大版八年级上册1 探索勾股定理精品教学ppt课件: 这是一份初中数学北师大版八年级上册<a href="/sx/tb_c10019_t3/?tag_id=26" target="_blank">1 探索勾股定理精品教学ppt课件</a>,文件包含北师大版数学八年级上册11探索勾股定理第2课时课件pptx、11探索勾股定理第2课时教案doc、11探索勾股定理第2课时同步练习docx、11探索勾股定理第2课时学案docx等4份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
北师大版八年级上册1 探索勾股定理教学课件ppt: 这是一份北师大版八年级上册<a href="/sx/tb_c10019_t3/?tag_id=26" target="_blank">1 探索勾股定理教学课件ppt</a>,共22页。PPT课件主要包含了学习目标,复习回顾,斜边的一半,探究新知,证明勾股定理,验证勾股定理,归纳总结,典型例题,随堂练习,课堂小结等内容,欢迎下载使用。
北师大版八年级上册1 探索勾股定理教学ppt课件: 这是一份北师大版八年级上册<a href="/sx/tb_c10019_t3/?tag_id=26" target="_blank">1 探索勾股定理教学ppt课件</a>,共22页。PPT课件主要包含了探索勾股定理,a-b,探究勾股定理等内容,欢迎下载使用。













