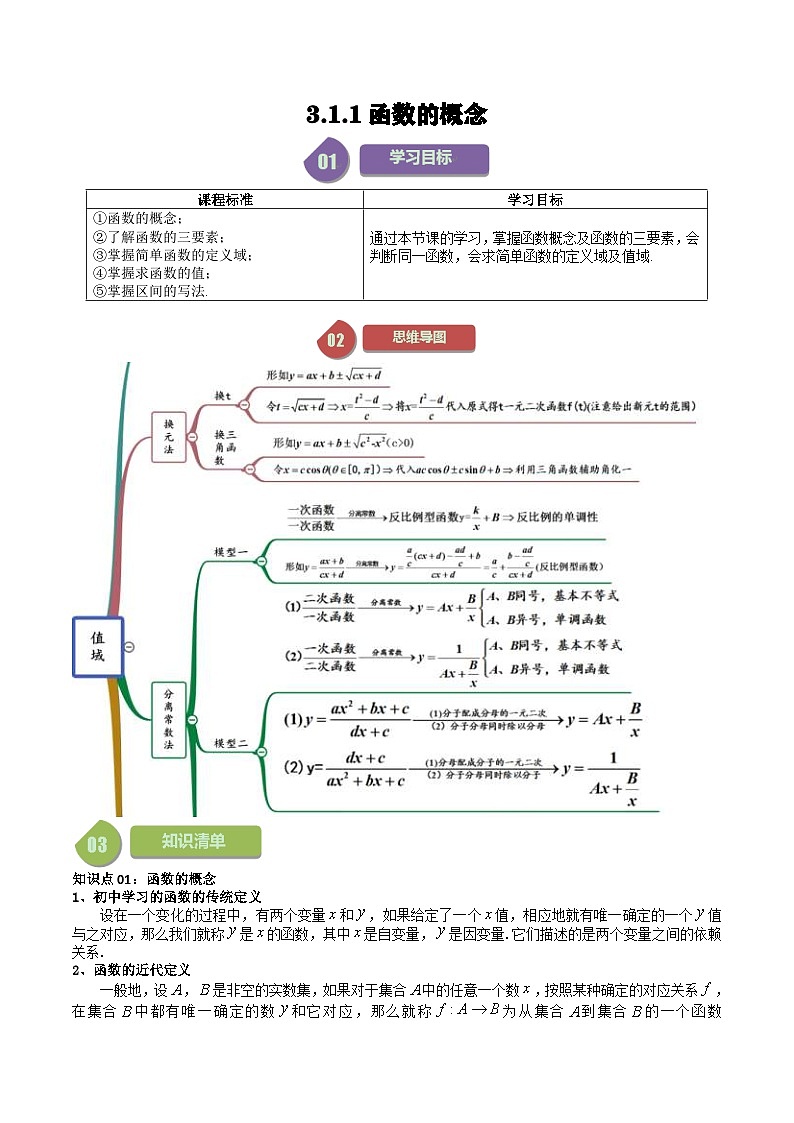
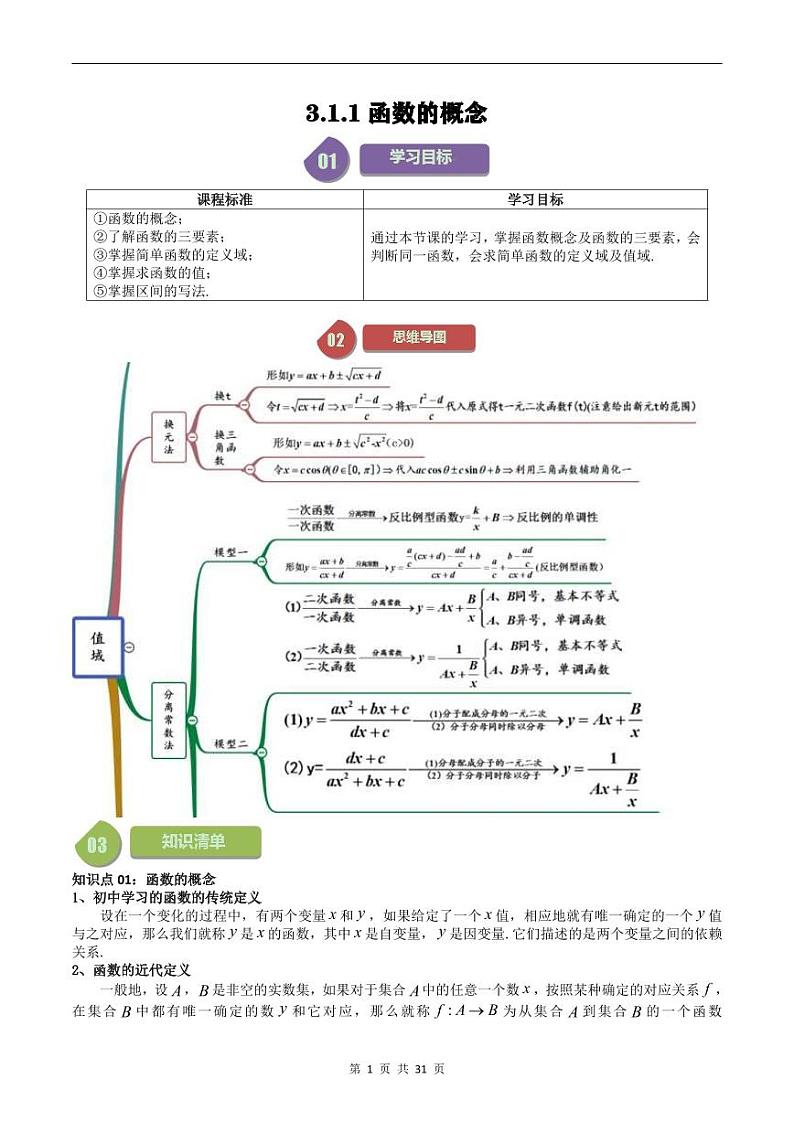
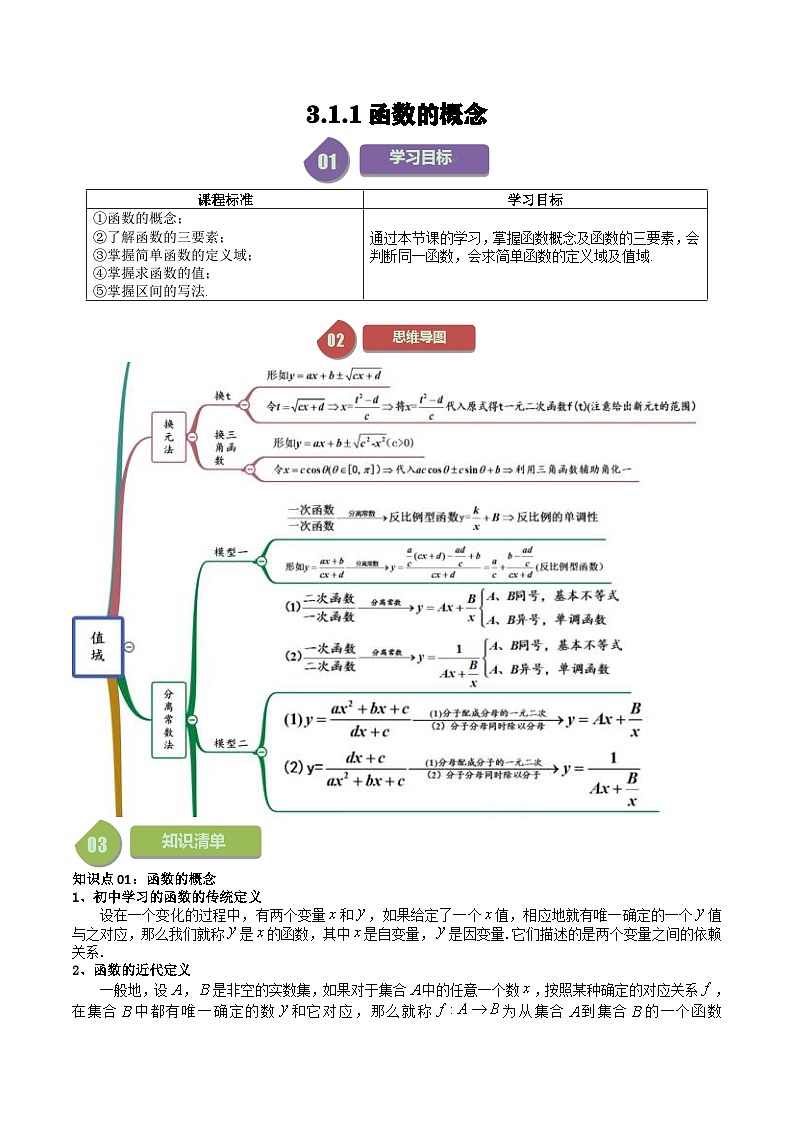
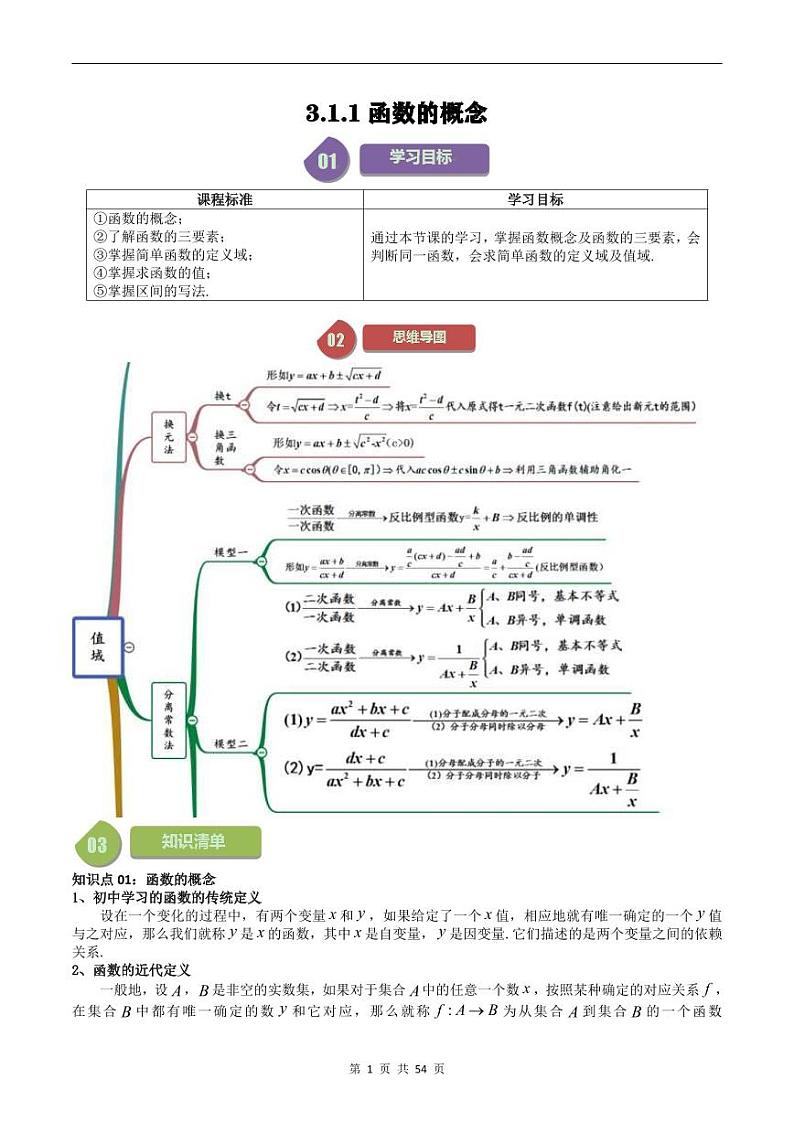
高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示精品习题

这是一份高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示精品习题，文件包含人教A版高中数学必修第一册同步讲义311函数的概念及其表示原卷版doc、人教A版高中数学必修第一册同步讲义311函数的概念及其表示原卷版pdf、人教A版高中数学必修第一册同步讲义311函数的概念及其表示教师版doc、人教A版高中数学必修第一册同步讲义311函数的概念及其表示教师版pdf等4份试卷配套教学资源，其中试卷共171页， 欢迎下载使用。


知识点01：函数的概念
1、初中学习的函数的传统定义
设在一个变化的过程中，有两个变量 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，如果给定了一个 SKIPIF 1 < 0 值，相应地就有唯一确定的一个 SKIPIF 1 < 0 值与之对应，那么我们就称 SKIPIF 1 < 0 是 SKIPIF 1 < 0 的函数，其中 SKIPIF 1 < 0 是自变量， SKIPIF 1 < 0 是因变量.它们描述的是两个变量之间的依赖关系.
2、函数的近代定义
一般地，设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是非空的实数集，如果对于集合 SKIPIF 1 < 0 中的任意一个数 SKIPIF 1 < 0 ，按照某种确定的对应关系 SKIPIF 1 < 0 ，在集合 SKIPIF 1 < 0 中都有唯一确定的数 SKIPIF 1 < 0 和它对应，那么就称 SKIPIF 1 < 0 为从集合 SKIPIF 1 < 0 到集合 SKIPIF 1 < 0 的一个函数(functin)，记作 SKIPIF 1 < 0 ， SKIPIF 1 < 0 .其中， SKIPIF 1 < 0 叫做自变量， SKIPIF 1 < 0 的取值范围 SKIPIF 1 < 0 叫做函数的定义域；与 SKIPIF 1 < 0 的值相对应的 SKIPIF 1 < 0 值叫做函数值，函数值的集合 SKIPIF 1 < 0 叫做函数的值域．显然，值域是集合 SKIPIF 1 < 0 的子集.
函数的四个特征：
①非空性： SKIPIF 1 < 0 ， SKIPIF 1 < 0 必须为非空数集（注意不仅非空，还要是数集），定义域或值域为空集的函数是不存在的.
②任意性：即定义域中的每一个元素都有函数值.
③单值性：每一个自变量有且仅有唯一的函数值与之对应（可以多对一，不能一对多）.
④方向性：函数是一个从定义域到值域的对应关系，如果改变这个对应方向，那么新的对应所确定
的关系就不一定是函数关系.
【即学即练1】（多选）下列四个图象中，是函数图象的是（ ）
A． B． C． D．
知识点02：函数的三要素
1、定义域：函数的定义域是自变量的取值范围．
2、对应关系：对应关系 SKIPIF 1 < 0 是函数的核心，它是对自变量 SKIPIF 1 < 0 实施“对应操作”的“程序”或者“方法”．
3、值域：与 SKIPIF 1 < 0 的值相对应的 SKIPIF 1 < 0 值叫做函数值，函数值的集合 SKIPIF 1 < 0 叫做函数的值域(range).
【即学即练2】函数 SKIPIF 1 < 0 的定义域为______．
知识点03：函数相等
同一函数：只有当两个函数的定义域和对应关系都分别相同时,这两个函数才相等,即是同一个函数.
【即学即练3】下列四组函数中，表示同一函数的是（ ）
A． SKIPIF 1 < 0 与 SKIPIF 1 < 0 B． SKIPIF 1 < 0 与 SKIPIF 1 < 0
C． SKIPIF 1 < 0 与 SKIPIF 1 < 0 D． SKIPIF 1 < 0 与 SKIPIF 1 < 0
知识点04：区间的概念
1区间的概念
设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是实数，且 SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 的实数 SKIPIF 1 < 0 的全体，叫做闭区间，
记作 SKIPIF 1 < 0 ，即， SKIPIF 1 < 0 。如图： SKIPIF 1 < 0 ， SKIPIF 1 < 0 叫做区间的端点．在数轴上表示一个区间时，若区间包括端点，则端点用实心点表示；若区间不包括端点，则端点用空心点表示．
2含有无穷大的表示
全体实数也可用区间表示为 SKIPIF 1 < 0 ，符号“ SKIPIF 1 < 0 ”读作“正无穷大”，“ SKIPIF 1 < 0 ”读作“负无穷大”，即 SKIPIF 1 < 0 。
【即学即练4】已知集合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型01 函数关系的判断
【典例1】若函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，值域为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的图象可能是（ ）
A．B．
C．D．
【典例2】已知集合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，下列对应关系中，从 SKIPIF 1 < 0 到 SKIPIF 1 < 0 的函数为（ ）
A．f： SKIPIF 1 < 0 B．f： SKIPIF 1 < 0
C．f： SKIPIF 1 < 0 D．f： SKIPIF 1 < 0
【变式1】（多选）下列对应中是函数的是（ ）．
A． SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0
B． SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0
C． SKIPIF 1 < 0 ，其中y为不大于x的最大整数， SKIPIF 1 < 0 ， SKIPIF 1 < 0
D． SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0
题型02 集合与区间的转化
【典例1】已知全集 SKIPIF 1 < 0 ,集合 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】若集合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式1】全集 SKIPIF 1 < 0 ，集合 SKIPIF 1 < 0 ，集合 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型03同一个函数
【典例1】下列各组函数表示相同函数的是（ ）
A． SKIPIF 1 < 0 和 SKIPIF 1 < 0 B． SKIPIF 1 < 0 和 SKIPIF 1 < 0
C． SKIPIF 1 < 0 和 SKIPIF 1 < 0 D． SKIPIF 1 < 0 和 SKIPIF 1 < 0
【典例2】（多选）下面各组函数表示同一函数的是（ ）
A． SKIPIF 1 < 0 ， SKIPIF 1 < 0 B． SKIPIF 1 < 0 （ SKIPIF 1 < 0 ）， SKIPIF 1 < 0
C． SKIPIF 1 < 0 ， SKIPIF 1 < 0 D． SKIPIF 1 < 0 ， SKIPIF 1 < 0
【变式1】下列每组中的函数是同一个函数的是（ ）
A． SKIPIF 1 < 0 ， SKIPIF 1 < 0 B． SKIPIF 1 < 0 ， SKIPIF 1 < 0
C． SKIPIF 1 < 0 ， SKIPIF 1 < 0 D． SKIPIF 1 < 0 ， SKIPIF 1 < 0
题型04 求函数值
【典例1】若函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 _________．
【典例2】若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ＝______．
【变式1】设函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式2】已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
（1）计算： SKIPIF 1 < 0 ____________；
（2）计算： SKIPIF 1 < 0 ____________．
题型05根据函数值请求自变量或参数
【典例1】若函数 SKIPIF 1 < 0 的值域是 SKIPIF 1 < 0 ，则此函数的定义域为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】（多选）若函数 SKIPIF 1 < 0 在定义域 SKIPIF 1 < 0 上的值域为 SKIPIF 1 < 0 ，则区间 SKIPIF 1 < 0 可能为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式1】已知函数 SKIPIF 1 < 0 的值域是 SKIPIF 1 < 0 ，则x的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型06函数的定义域（具体函数的定义域）
【典例1】已知函数 SKIPIF 1 < 0 的定义域为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】函数 SKIPIF 1 < 0 的定义域为______．
【变式1】函数 SKIPIF 1 < 0 的定义域为________.
题型07函数的定义域（抽象函数的定义域）
【典例1】已知函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的定义域为______.
【典例2】若 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的定义域．
【变式1】（1）已知函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的定义域为______．
（2）已知函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的定义域为______．
题型08 函数的定义域（复合函数的定义域）
【典例1】若函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的定义域为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】已知函数 SKIPIF 1 < 0 ）的定义域为 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的定义域为（ ）
A．（ SKIPIF 1 < 0 ，4） B．[ SKIPIF 1 < 0 ，4） C．（ SKIPIF 1 < 0 ，6） D．（ SKIPIF 1 < 0 ，2）
【变式1】已知函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的定义域为______.
题型09 函数的定义域（实际问题中的定义域）
【典例1】已知等腰三角形的周长为 SKIPIF 1 < 0 ，底边长 SKIPIF 1 < 0 是腰长 SKIPIF 1 < 0 的函数，则函数的定义域为( )
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】周长为定值 SKIPIF 1 < 0 的矩形，它的面积 SKIPIF 1 < 0 是这个矩形的一边长 SKIPIF 1 < 0 的函数，则这个函数的定义域是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式1】如图，某小区有一块底边和高均为40m的锐角三角形空地，现规划在空地内种植一边长为 SKIPIF 1 < 0 （单位：m）的矩形草坪（阴影部分），要求草坪面积不小于 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围为______.
题型10函数的值域（常见（一次，二次，反比例）函数的值域）
【典例1】函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值域为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】求下列函数的定义域、值域，并画出图象：
(1) SKIPIF 1 < 0 ； (2) SKIPIF 1 < 0 ； (3) SKIPIF 1 < 0 ；
(4) SKIPIF 1 < 0 ； (5) SKIPIF 1 < 0 ； (6) SKIPIF 1 < 0 ．
【变式1】例题3．求下列函数的值域.
(1) SKIPIF 1 < 0 ; (2) SKIPIF 1 < 0 , SKIPIF 1 < 0 .
题型11函数的值域（根式型函数的值域）
【典例1】函数 SKIPIF 1 < 0 的值域为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】求函数 SKIPIF 1 < 0 的值域为_________.
【变式1】函数 SKIPIF 1 < 0 的值域是___________.
题型12函数的值域（分式型函数的值域）
【典例1】函数y SKIPIF 1 < 0 的值域是（ ）
A．（﹣∞，+∞）B．（﹣∞， SKIPIF 1 < 0 ）∪（ SKIPIF 1 < 0 ，+∞）
C．（﹣∞， SKIPIF 1 < 0 ）∪（ SKIPIF 1 < 0 ，+∞）D．（﹣∞， SKIPIF 1 < 0 ）∪（ SKIPIF 1 < 0 ，+∞）
【典例2】（1）求函数 SKIPIF 1 < 0 的值域；
（2）求函数 SKIPIF 1 < 0 的值域.
【变式1】求函数 SKIPIF 1 < 0 的值域______________．
【变式2】函数 SKIPIF 1 < 0 的值域是___________.
题型13根据函数的值域求定义域
【典例1】已知函数 SKIPIF 1 < 0 的值域是 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】（多选）已知函数 SKIPIF 1 < 0 的值域是 SKIPIF 1 < 0 ，则其定义域可能是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式1】（多选）若函数 SKIPIF 1 < 0 在定义域 SKIPIF 1 < 0 上的值域为 SKIPIF 1 < 0 ，则区间 SKIPIF 1 < 0 可能为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型14重点方法之换元法求值域
【典例1】函数 SKIPIF 1 < 0 的值域为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】求函数 SKIPIF 1 < 0 的值域.
题型15重点方法之分离常数法求值域
【典例1】求函数 SKIPIF 1 < 0 的值域.
【典例2】求下列函数的值域： SKIPIF 1 < 0
题型16数学思想方法（数形结合的思想方法）
【典例1】已知函数 SKIPIF 1 < 0 的值域是 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】若函数 SKIPIF 1 < 0 的定义域是 SKIPIF 1 < 0 ，则其值域为（ ）.
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型17易错题（换元必换范围）
【典例1】求下列函数的值域： SKIPIF 1 < 0 ．
【典例2】函数 SKIPIF 1 < 0 的值域为___________．
3.1.1函数的概念
A夯实基础
一、单选题
1．已知函数 SKIPIF 1 < 0 ，那么 SKIPIF 1 < 0 的值（ ）
A．3B．5C．7
2．函数 SKIPIF 1 < 0 的定义域是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0 或 SKIPIF 1 < 0
3．下列各函数中，与函数 SKIPIF 1 < 0 表示同一函数的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
4．已知高斯取整函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）
A．2B．3C．4D．5
5．下表给出了x与 SKIPIF 1 < 0 和 SKIPIF 1 < 0 的对应关系，根据表格可知 SKIPIF 1 < 0 的值为（ ）
A．1B．2C．3D．4
6．下列对应是从集合A到集合B的函数的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
7．若函数 SKIPIF 1 < 0 的定义域是 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的定义域是（ ）
A．[-4，1]B．[-3，1]C．[-3，1）D．[-4，1）
8．函数 SKIPIF 1 < 0 的值域为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
二、多选题
9．若函数 SKIPIF 1 < 0 定义域为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则下列结果正确的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
10．中国清朝数学家李善兰在1859年翻译《代数学》中首次将“functin”译做：“函数”，沿用至今，为什么这么翻译，书中解释说“凡此变数中函彼变数者，则此为彼之函数”．1930年美国人给出了我们课本中所学的集合论的函数定义．已知集合M＝{ SKIPIF 1 < 0 1，1，2，4}，N＝{1，2，4，16}，给出下列四个对应法则，请由函数定义判断，其中能构成从M到N的函数的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
三、填空题
11．设二次函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）的值域是 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值是____________．
12．函数 SKIPIF 1 < 0 的值域为___________．
四、解答题
13．已知函数 SKIPIF 1 < 0 的定义域为A，集合 SKIPIF 1 < 0 .
(1)当 SKIPIF 1 < 0 时，求 SKIPIF 1 < 0 ；
(2)若 SKIPIF 1 < 0 ，求a的取值范围.
14．已知函数 SKIPIF 1 < 0 的值域为[1，3]，求 SKIPIF 1 < 0 的值
B能力提升
1．若函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，值域为 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．函数 SKIPIF 1 < 0 的值域为
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．设 SKIPIF 1 < 0 ，用 SKIPIF 1 < 0 表示不超过 SKIPIF 1 < 0 的最大整数，则 SKIPIF 1 < 0 称为高斯函数．例如： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，已知函数 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的值域为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
4．已知函数 SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的值；
(2)求证： SKIPIF 1 < 0 的定值；
(3)求 SKIPIF 1 < 0 的值．
C综合素养
1．欧拉函数 SKIPIF 1 < 0 的函数值等于所有不超过正整数 SKIPIF 1 < 0 ，且与 SKIPIF 1 < 0 互素的正整数的个数，例如， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．若 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．（多选）对于定义域为 SKIPIF 1 < 0 的函数 SKIPIF 1 < 0 ，若同时满足下列条件：① SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则称函数 SKIPIF 1 < 0 为“ SKIPIF 1 < 0 函数”.下列结论正确的是（ ）
A．若 SKIPIF 1 < 0 为“ SKIPIF 1 < 0 函数”，则其图象恒过定点 SKIPIF 1 < 0
B．函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是“ SKIPIF 1 < 0 函数”
C．函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是“ SKIPIF 1 < 0 函数”（ SKIPIF 1 < 0 表示不大于 SKIPIF 1 < 0 的最大整数）
D．若 SKIPIF 1 < 0 为“ SKIPIF 1 < 0 函数”，则 SKIPIF 1 < 0 一定是 SKIPIF 1 < 0 上的增函数
3．已知定义域为 SKIPIF 1 < 0 的函数 SKIPIF 1 < 0 ，对于任意的 SKIPIF 1 < 0 恒有 SKIPIF 1 < 0 .
(1)若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值；
(2)若 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的值.
4．如果一个函数的值域与其定义域相同，则称该函数为“同域函数”.已知函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 且 SKIPIF 1 < 0 .
（Ⅰ）若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的定义域；
（Ⅱ）当 SKIPIF 1 < 0 时，若 SKIPIF 1 < 0 为“同域函数”，求实数 SKIPIF 1 < 0 的值；
（Ⅲ）若存在实数 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0 为“同域函数”，求实数 SKIPIF 1 < 0 的取值范围.
3.1.2函数的表示法
知识点01：函数的表示法
1、解析法：用数学表达式表示两个变量之间的对应关系.
2、列表法：列出表格来表示两个变量之间的对应关系.
3、图象法：用图象表示两个变量之间的对应关系.
知识点02：求函数解析式
1、待定系数法：若已知函数的类型（如一次函数、二次函数，反比例等），可用待定系数法．
2、换元法：主要用于解决已知 SKIPIF 1 < 0 这类复合函数的解析式，求函数 SKIPIF 1 < 0 的解析式的问题，在使用换元法时特别注意，换元必换范围.
3、配凑法：由已知条件 SKIPIF 1 < 0 ，可将 SKIPIF 1 < 0 改写成关于 SKIPIF 1 < 0 的表达式，
4、方程组（消去）法：主要解决已知 SKIPIF 1 < 0 与 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ……的方程，求 SKIPIF 1 < 0 解析式。
【即学即练1】已知 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 _______， SKIPIF 1 < 0 =_______．
知识点03：分段函数
对于函数 SKIPIF 1 < 0 ，若自变量在定义域内的在不同范围取值时，函数的对应关系也不相同，则称函数 SKIPIF 1 < 0 叫分段函数．
注：(1)分段函数是一个函数，只是自变量在不同范围取值时，函数的对应关系不相同；
（2）在书写时要指明各段函数自变量的取值范围；
（3）分段函数的定义域是所以自变量取值区间的并集．
【即学即练2】已知函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 _________．
知识点04：函数的图象
1、函数图象的平移变换（左“+”右“-”；上“+”下“-”）
① SKIPIF 1 < 0
② SKIPIF 1 < 0
③ SKIPIF 1 < 0
④ SKIPIF 1 < 0
注：左右平移只能单独一个 SKIPIF 1 < 0 加或者减，注意当 SKIPIF 1 < 0 前系数不为1,需将系数提取到外面.
2、函数图象的对称变换
① SKIPIF 1 < 0 的图象 SKIPIF 1 < 0 SKIPIF 1 < 0 的图象；
② SKIPIF 1 < 0 的图象 SKIPIF 1 < 0 SKIPIF 1 < 0 的图象；
③ SKIPIF 1 < 0 的图象 SKIPIF 1 < 0 SKIPIF 1 < 0 的图象；
3、函数图象的翻折变换（绝对值变换）
① SKIPIF 1 < 0 的图象 SKIPIF 1 < 0 SKIPIF 1 < 0 的图象；
（口诀；以 SKIPIF 1 < 0 轴为界，保留 SKIPIF 1 < 0 轴上方的图象；将 SKIPIF 1 < 0 轴下方的图象翻折到 SKIPIF 1 < 0 轴上方）
② SKIPIF 1 < 0 的图象 SKIPIF 1 < 0 SKIPIF 1 < 0 的图象.
（口诀；以 SKIPIF 1 < 0 轴为界，去掉 SKIPIF 1 < 0 轴左侧的图象，保留 SKIPIF 1 < 0 轴右侧的图象；将 SKIPIF 1 < 0 轴右侧图象翻折到 SKIPIF 1 < 0 轴左侧；本质是个偶函数）
【即学即练3】函数 SKIPIF 1 < 0 的部分图象大致是（ ）
A． B． C． D．
题型01 函数的三种表示法的应用
【典例1】已知边长为1的正方形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点，动点 SKIPIF 1 < 0 在正方形 SKIPIF 1 < 0 边上沿 SKIPIF 1 < 0 运动．设点 SKIPIF 1 < 0 经过的路程为 SKIPIF 1 < 0 ． SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ．则 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的函数图象大致为图中的（ ）
A． B． C． D．
【典例2】如图中的图象所表示的函数的解析式为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例3】已知函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别由下表给出，
则 SKIPIF 1 < 0 _____________；满足 SKIPIF 1 < 0 的 SKIPIF 1 < 0 的值是_____________．
【变式1】如图， SKIPIF 1 < 0 是边长为2的等边三角形，点 SKIPIF 1 < 0 由点 SKIPIF 1 < 0 沿线段 SKIPIF 1 < 0 向点 SKIPIF 1 < 0 移动，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 的垂线 SKIPIF 1 < 0 ，设 SKIPIF 1 < 0 ，记位于直线 SKIPIF 1 < 0 左侧的图形的面积为 SKIPIF 1 < 0 ，那么 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的函数关系的图象大致是（ ）
A． B． C． D．
【变式2】某校要召开学生代表大会，规定各班每 SKIPIF 1 < 0 人推选一名代表，当班人数除以 SKIPIF 1 < 0 的余数大于 SKIPIF 1 < 0 时，再增选一名代表，则各班推选代表人数 SKIPIF 1 < 0 与该班人数 SKIPIF 1 < 0 之间的函数关系用取整函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 表示不大于 SKIPIF 1 < 0 的最大整数，如 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）可表示为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型02求函数的解析式（待定系数法）
【典例1】（多选）已知函数 SKIPIF 1 < 0 是一次函数，满足 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的解析式可能为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】若二次函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的表达式为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式1】若 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A．3B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型03求函数的解析式（换元法）
【典例1】已知 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的解析式为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】已知 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 .
题型04求函数的解析式（配凑法）
【典例1】已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 _______．
【典例2】已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A．6B．3C．11D．10
题型05求函数的解析式（方程组（消去）法）
【典例1】已知函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，对任意 SKIPIF 1 < 0 均满足： SKIPIF 1 < 0 则函数 SKIPIF 1 < 0 解析式为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】已知 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的解析式
【变式1】已知函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ．
(1)求 SKIPIF 1 < 0 的解析式；
(2)设函数 SKIPIF 1 < 0 ，若对任意 SKIPIF 1 < 0 ， SKIPIF 1 < 0 恒成立，求实数m的取值范围．
题型06求函数的解析式（赋值法求抽象函数的解析式）
【典例1】定义在 SKIPIF 1 < 0 上的函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，并且对任意实数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 都有 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的解析式.
【典例2】已知函数 SKIPIF 1 < 0 满足：对一切实数 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，均有 SKIPIF 1 < 0 成立，且 SKIPIF 1 < 0 ．
求函数 SKIPIF 1 < 0 的表达式；
【变式1】写出一个满足： SKIPIF 1 < 0 的函数解析式为______.
【变式2】已知函数 SKIPIF 1 < 0 对一切的实数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，都满足 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 .
（1）求 SKIPIF 1 < 0 的值；
（2）求 SKIPIF 1 < 0 的解析式；
（3）求 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的值域.
题型07 分段函数（求分段函数的值）
【典例1】已知函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ______．
【典例2】已知函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为______.
题型08 分段函数（已知分段函数的值求参数）
【典例1】已知函数 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 的最小值为1，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】已知函数 SKIPIF 1 < 0 无最大值，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例3】已知函数 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最大值是________．
题型09 分段函数（分段函数的值域或最值）
【典例1】函数 SKIPIF 1 < 0 的最小值是__________.
【典例2】已知函数 SKIPIF 1 < 0 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ______．
【变式1】（多选）设函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 存在最小值时，实数 SKIPIF 1 < 0 的值可能是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C．0D．1
题型10 分段函数（解分段不等式）
【典例1】设 SKIPIF 1 < 0 ，则不等式 SKIPIF 1 < 0 的解集是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】函数 SKIPIF 1 < 0 ，若关于 SKIPIF 1 < 0 的不等式 SKIPIF 1 < 0 的解集___________.
【变式1】已知 SKIPIF 1 < 0 ,则使 SKIPIF 1 < 0 成立的 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式2】已知函数 SKIPIF 1 < 0 .
(1)求 SKIPIF 1 < 0 的最小值；
(2)若 SKIPIF 1 < 0 对任意 SKIPIF 1 < 0 恒成立，求k的取值范围.
题型11函数图象（函数图象识别）
【典例1】设 SKIPIF 1 < 0 均为非零实数，则直线 SKIPIF 1 < 0 和 SKIPIF 1 < 0 在同一坐标系下的图形可能是（ ）．
A． B． C． D．
【典例2】函数 SKIPIF 1 < 0 的图象大致形状是（ ）
A． B． C． D．
【变式1】已知函数 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的图像是（ ）
A． B． C． D．
题型12函数图象（画出具体函数图象）
【典例1】给定函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
(1)在所给坐标系（1）中画出函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的大致图象；（不需列表，直接画出.）
(2) SKIPIF 1 < 0 ，用 SKIPIF 1 < 0 表示 SKIPIF 1 < 0 ， SKIPIF 1 < 0 中的较小者，记为 SKIPIF 1 < 0 ，请分别用解析法和图象法表示函数 SKIPIF 1 < 0 .（ SKIPIF 1 < 0 的图象画在坐标系（2）中）
(3)直接写出函数 SKIPIF 1 < 0 的值域.
【典例2】已知函数 SKIPIF 1 < 0 .
（1）若 SKIPIF 1 < 0 ，求实数 SKIPIF 1 < 0 的值；
（2）画出函数的图象并写出函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上的值域；
（3）若函数 SKIPIF 1 < 0 ，求函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上最大值.
【变式1】已知函数 SKIPIF 1 < 0 ，其中[x]表示不超过 SKIPIF 1 < 0 的最大整数，例如 SKIPIF 1 < 0
(1)将 SKIPIF 1 < 0 的解析式写成分段函数的形式;
(2)请在如图所示的平面直角坐标系中作出函数 SKIPIF 1 < 0 的图象;
(3)根据图象写出函数 SKIPIF 1 < 0 的值域.
题型13函数图象（根据实际问题做出函数图象）
【典例1】如图为某无人机飞行时，从某时刻开始15分钟内的速度 SKIPIF 1 < 0 （单位：米/分钟）与时间 SKIPIF 1 < 0 （单位：分钟）的关系．若定义“速度差函数” SKIPIF 1 < 0 为无人机在时间段 SKIPIF 1 < 0 内的最大速度与最小速度的差，则 SKIPIF 1 < 0 的图像为（ ）
A． B． C． D．
【典例2】如图，点 SKIPIF 1 < 0 在边长为1的正方形的边上运动， SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中点，则当 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 运动时，点 SKIPIF 1 < 0 经过的路程 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 的函数 SKIPIF 1 < 0 的图象大致是下图中的
A． B． C． D．
【变式1】如图，公园里有一处扇形花坛，小明同学从 SKIPIF 1 < 0 点出发，沿花坛外侧的小路顺时针方向匀速走了一圈(路线为 SKIPIF 1 < 0 )，则小明到 SKIPIF 1 < 0 点的直线距离 SKIPIF 1 < 0 与他从 SKIPIF 1 < 0 点出发后运动的时间 SKIPIF 1 < 0 之间的函数图象大致是（ ）
A． B． C． D．
题型14函数图象（函数图象的变换）
【典例1】（多选）下列函数图像经过变换后，过原点的是（ ）
A． SKIPIF 1 < 0 向右平移 SKIPIF 1 < 0 个单位B． SKIPIF 1 < 0 向左平移 SKIPIF 1 < 0 个单位
C． SKIPIF 1 < 0 向上平移 SKIPIF 1 < 0 个单位D． SKIPIF 1 < 0 向下平移 SKIPIF 1 < 0 个单位
【典例2】已知函数 SKIPIF 1 < 0 定义在 SKIPIF 1 < 0 上的图象如图所示，请分别画出下列函数的图象：

(1) SKIPIF 1 < 0 ；(2) SKIPIF 1 < 0 ；(3) SKIPIF 1 < 0 ；(4) SKIPIF 1 < 0 ；(5) SKIPIF 1 < 0 ；(6) SKIPIF 1 < 0 .
【变式1】将函数 SKIPIF 1 < 0 的图象向左平移1个单位，再向下平移3个单位长度，所得的函数图象对应的解析式为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型15函数图象（根据图象选择解析式）
【典例1】我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．”在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来研究函数图象的特征．我们从这个商标 中抽象出一个图象如图，其对应的函数可能是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】若函数 SKIPIF 1 < 0 的大致图象如图所示，则 SKIPIF 1 < 0 的解析式可能是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式1】已知某函数 SKIPIF 1 < 0 的部分图象如图所示，则下列函数解析式符合该图象特征的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型16新定义（新文化题）
【典例1】十九世纪德国数学家狄利克雷提出了“狄利克雷函数” SKIPIF 1 < 0 它在现代数学的发展过程中有着重要意义，若函数 SKIPIF 1 < 0 ，则下列实数不属于函数 SKIPIF 1 < 0 值域的是（ ）
A．3B．2C．1D．0
【典例2】黎曼函数是一个特殊的函数，由德国著名的数学家波恩哈德·黎曼发现提出，在高等数学中有着广泛的应用.其定义黎曼函数 SKIPIF 1 < 0 为：当 SKIPIF 1 < 0 （ SKIPIF 1 < 0 为正整数， SKIPIF 1 < 0 是既约真分数）时 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 或 SKIPIF 1 < 0 或 SKIPIF 1 < 0 为 SKIPIF 1 < 0 上的无理数时 SKIPIF 1 < 0 .已知 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 都是区间 SKIPIF 1 < 0 内的实数，则下列不等式一定正确的是
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【变式1】高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德，牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：对于实数 SKIPIF 1 < 0 ，符号 SKIPIF 1 < 0 表示不超过 SKIPIF 1 < 0 的最大整数，则 SKIPIF 1 < 0 称为高斯函数，例如 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，定义函数 SKIPIF 1 < 0 ，则下列命题中正确的序号是________．
①函数 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ； ②函数 SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 ；
③函数 SKIPIF 1 < 0 的图象与直线 SKIPIF 1 < 0 有无数个交点 ④ SKIPIF 1 < 0
题型17重点方法（换元法）
【典例1】若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ＝________.
【典例2】已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ______．
【变式2】已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ___________.
题型18重点方法（消去法）
【典例1】若函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A．0B．2C．3D． SKIPIF 1 < 0
【典例2】已知函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 __________.
【变式1】已知 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的解析式为___________.
题型19数学思想方法（数形结合法）
【典例1】（多选）已知函数 SKIPIF 1 < 0 ， 关于函数 SKIPIF 1 < 0 的结论正确的是（ ）
A． SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 B． SKIPIF 1 < 0 的值域为 SKIPIF 1 < 0
C． SKIPIF 1 < 0 D．若 SKIPIF 1 < 0 ， 则 SKIPIF 1 < 0 的值是 SKIPIF 1 < 0
【典例2】已知定义在 SKIPIF 1 < 0 上的函数 SKIPIF 1 < 0 ，下列结论正确的为（ ）
A．函数 SKIPIF 1 < 0 的值域为 SKIPIF 1 < 0
B．存在 SKIPIF 1 < 0 ，使得不等式 SKIPIF 1 < 0 成立
C．当 SKIPIF 1 < 0 时，函数的图象与 SKIPIF 1 < 0 轴围成的面积为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
D．当 SKIPIF 1 < 0 时， SKIPIF 1 < 0
【变式1】对于实数 SKIPIF 1 < 0 ，符号 SKIPIF 1 < 0 表示不超过 SKIPIF 1 < 0 的最大整数，例如 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，定义函数 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的值域为________.
题型20易错题（换元必换范围）
【典例1】（多选）若函数 SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【典例2】已知 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 的解析式是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 （ SKIPIF 1 < 0 且 SKIPIF 1 < 0 ）
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3.1.2函数的表示法
A夯实基础
一、单选题
1．已知函数 SKIPIF 1 < 0 的部分x与y的对应关系如下表：
则 SKIPIF 1 < 0 （ ）
A．－1B．－2
C．－3D．3
2．设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值为（ ）
A．9B．11C．28D．14
3．一次函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的解析式为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
4．已知函数 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．已知函数 SKIPIF 1 < 0 的值域是 SKIPIF 1 < 0 ，则x的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．已知 SKIPIF 1 < 0 ，并且m、n是方程 SKIPIF 1 < 0 的两根，则实数a、b、m、n的大小关系可能是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
7．设函数 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B．1C． SKIPIF 1 < 0 D．2
8．如图所示，在直角梯形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点E由B沿折线 SKIPIF 1 < 0 向点D移动， SKIPIF 1 < 0 ，垂足为M， SKIPIF 1 < 0 ，垂足为N，设 SKIPIF 1 < 0 ，矩形 SKIPIF 1 < 0 的面积为y，那么y与x的函数关系图像大致是（ ）
A． B． C． D．
二、多选题
9．下列函数中，满足 SKIPIF 1 < 0 的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
10．已知 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
三、填空题
11．已知函数 SKIPIF 1 < 0 若 SKIPIF 1 < 0 ，则实数 SKIPIF 1 < 0 的值为______.
12．已知函数 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，则不等式 SKIPIF 1 < 0 的解集是__________
四、解答题
13．已知函数 SKIPIF 1 < 0 （a，b为常数）且方程 SKIPIF 1 < 0 有两个实根为 SKIPIF 1 < 0 ．
(1)求函数 SKIPIF 1 < 0 的解析式；
(2)设 SKIPIF 1 < 0 ，解关于x的不等式： SKIPIF 1 < 0 ．
14．随着我国经济发展、医疗消费需求增长、人们健康观念转变以及人口老龄化进程加快等影响，医疗器械市场近年来一直保持了持续增长的趋势．某医疗器械公司为了进一步增加市场力，计划改进技术生产某产品．已知生产该产品的年固定成本为300万元，最大产能为100台，每生产 SKIPIF 1 < 0 台，需另投入成本 SKIPIF 1 < 0 万元，且 SKIPIF 1 < 0 ，由市场调研知，该产品每台的售价为200万元，且全年内生产的该产品当年能全部销售完．
(1)写出年利润 SKIPIF 1 < 0 万元关于年产量 SKIPIF 1 < 0 台的函数解析式（利润=销售收入-成本）；
(2)当该产品的年产量为多少时，公司所获利润最大？最大利润是多少？
B能力提升
1．已知二次函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 的最大值是8，则此二次函数的解析式为 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．设函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 ，且当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .则不等式 SKIPIF 1 < 0 的解集是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．某校要召开学生代表大会，规定各班每 SKIPIF 1 < 0 人推选一名代表，当班人数除以 SKIPIF 1 < 0 的余数大于 SKIPIF 1 < 0 时，再增选一名代表，则各班推选代表人数 SKIPIF 1 < 0 与该班人数 SKIPIF 1 < 0 之间的函数关系用取整函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 表示不大于 SKIPIF 1 < 0 的最大整数，如 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）可表示为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
4．水培植物需要一种植物专用营养液，已知每投放 SKIPIF 1 < 0 且 SKIPIF 1 < 0 个单位的营养液，它在水中释放的浓度 SKIPIF 1 < 0 克/升 SKIPIF 1 < 0 随着时间 SKIPIF 1 < 0 天 SKIPIF 1 < 0 变化的函数关系式近似为 SKIPIF 1 < 0 ，其中 SKIPIF 1 < 0 ，若多次投放，则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和，根据经验，当水中营养液的浓度不低于 SKIPIF 1 < 0 克/升 SKIPIF 1 < 0 时，它才能有效．
(1)若只投放一次4个单位的营养液，则有效时间最多可能持续几天？
(2)若先投放2个单位的营养液，6天后再投放 SKIPIF 1 < 0 个单位的营养液，要使接下来的4天中，营养液能够持续有效，试求 SKIPIF 1 < 0 的最小值．
C综合素养
1．设集合 SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B．（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ） C． SKIPIF 1 < 0 D．（ SKIPIF 1 < 0 ，1]
2．（多选）函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有定义，若对任意 SKIPIF 1 < 0 ，都有 SKIPIF 1 < 0 ，则称 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上具有性质P.设 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上具有性质 SKIPIF 1 < 0 ，则下列命题正确的有（ ）
A． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的图象是连续不断的
B． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上具有性质 SKIPIF 1 < 0
C．若 SKIPIF 1 < 0 在 SKIPIF 1 < 0 处取得最小值1，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0
D．对任意 SKIPIF 1 < 0 ，有 SKIPIF 1 < 0
3．（多选）在数学中，布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理，它可应用到有限维空间，并构成一般不动点定理的基石，布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔（LEJBruwer），简单的讲就是对于满足一定条件的图象不间断的函数 SKIPIF 1 < 0 ，存在一个点 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 ，那么我们称该函数为“不动点”函数， SKIPIF 1 < 0 为函数的不动点，则下列说法正确的（ ）
A． SKIPIF 1 < 0 为“不动点”函数
B． SKIPIF 1 < 0 的不动点为 SKIPIF 1 < 0
C． SKIPIF 1 < 0 为“不动点”函数
D．若定义在R上有且仅有一个不动点的函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
4．已知函数y=f（x）和y=g（x）在[-2，2]的图像如图所示，给出下列四个命题：
①方程f[g（x）]=0有且仅有6个根
②方程g[f（x）]=0有且仅有3个根
③方程f[f（x）]=0有且仅有5个根
④方程g[g（x）]=0有且仅有4个根
其中正确的命题是___
5．已知二次函数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 .
(1)求 SKIPIF 1 < 0 的解析式；
(2)设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的最小值 SKIPIF 1 < 0 .
课程标准
学习目标
①函数的概念；
②了解函数的三要素；
③掌握简单函数的定义域；
④掌握求函数的值；
⑤掌握区间的写法.
通过本节课的学习，掌握函数概念及函数的三要素，会判断同一函数，会求简单函数的定义域及值域.
集合
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
区间
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
集合
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
区间
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
x
1
2
3
4
x
1
2
3
4
SKIPIF 1 < 0
3
1
4
2
SKIPIF 1 < 0
4
3
2
1
课程标准
学习目标
①了解函数的三种表示方法及特点；
②掌握求函数解析式的常用方法
③了解与认识分段函数及其定义域
④会用分析法与图象法表示分段函数，并能掌握分段函数的相关性质.
通过本节课的学习，熟练掌握函数的三种表示方法，会求函数的解析式，掌握分段函数的解析法与图象法的表示方法与性质.
优点
缺点
联系
解析法
①简明、全面的概括了变量之间的关系；
②可以通过解析式求出在定义域内任意自变量所对应的函数值；
③便于利用解析式研究函数的性质；
①并不是所有的函数都有解析式；
②不能直观地观察到函数的变化规律；
解析法、图象法、列表法各有各的优缺点，面对实际情境时，我们要根据不同的需要选择恰当的方法表示函数．
图象法
①能直观、形象地表示自变量的变化情况及相适应的函数值的变化趋势；
②可以直接应用图象来研究函数的性质；
①并不是所有的函数都能画出图象；
②不能精确地求出某一自变量相应的函数值；
列表法
①不需要计算就可以直接看出与自变量的值对应的函数值；
①不够全面，只能表示自变量取较少的有限值的对应关系；
②不能明显地展示出因变量随自变量变化的规律；
SKIPIF 1 < 0
0
1
2
SKIPIF 1 < 0
1
2
1
SKIPIF 1 < 0
0
1
2
SKIPIF 1 < 0
2
1
0
x
－3
－2
－1
0
1
2
3
4
y
3
2
1
0
0
－1
－2
－3