高中数学人教A版 (2019)必修 第一册第五章 三角函数5.1 任意角和弧度制5.1.2 弧度制优秀课堂检测

这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数5.1 任意角和弧度制5.1.2 弧度制优秀课堂检测，文件包含人教A版高中数学必修第一册同步讲义51任意角和弧度制原卷版doc、人教A版高中数学必修第一册同步讲义51任意角和弧度制原卷版pdf、人教A版高中数学必修第一册同步讲义51任意角和弧度制教师版doc、人教A版高中数学必修第一册同步讲义51任意角和弧度制教师版pdf等4份试卷配套教学资源，其中试卷共86页， 欢迎下载使用。


知识点01：任意角
1、角的概念
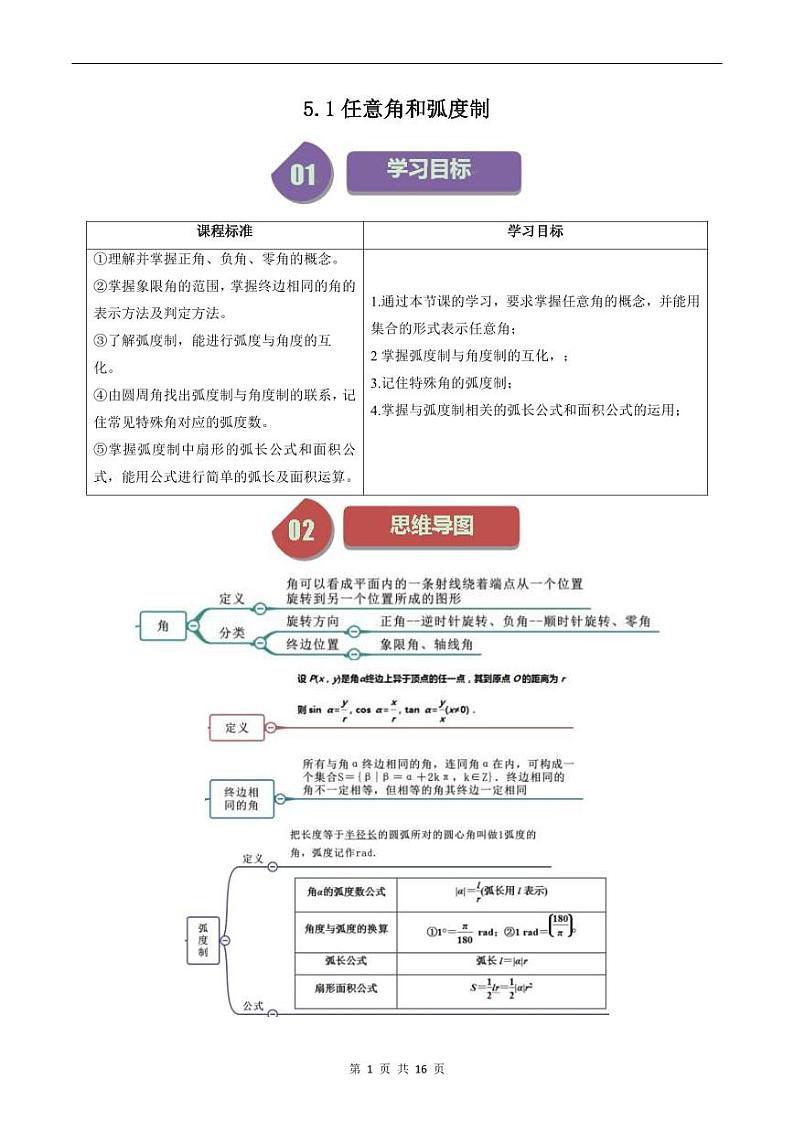
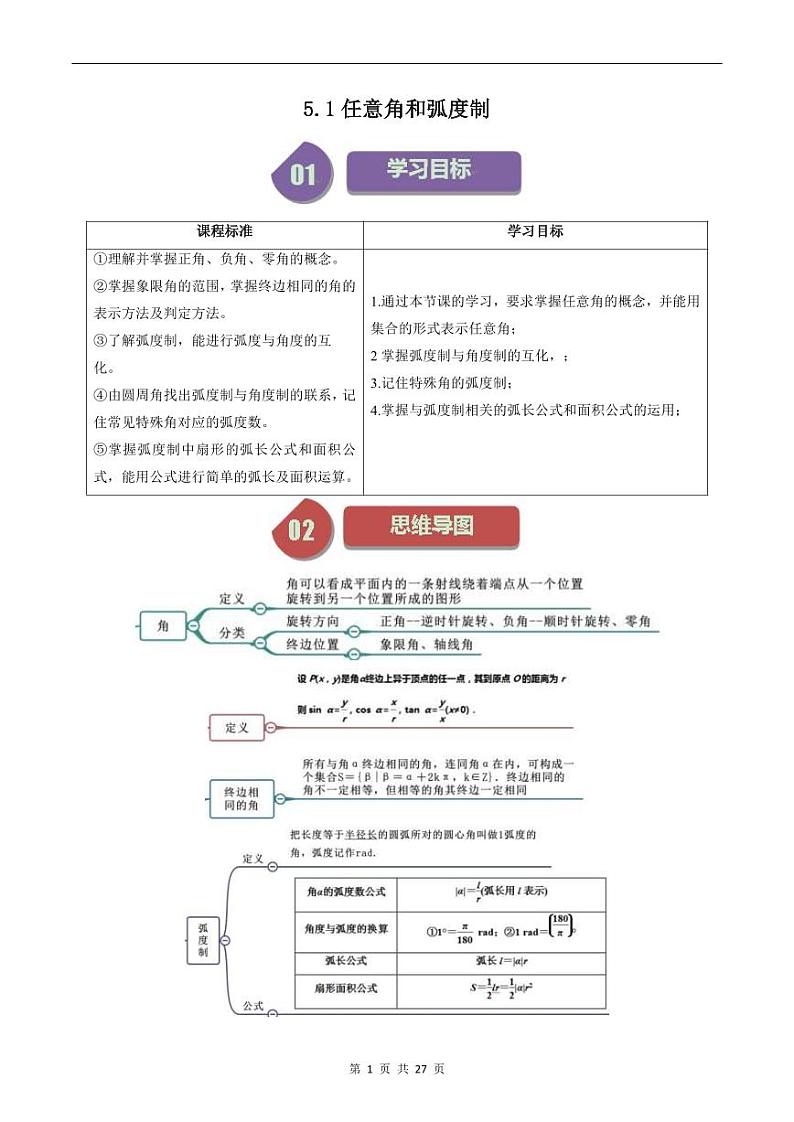
角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形
2、角的分类
①正角:按逆时针方向旋转所形成的角.
②负角:按顺时针方向旋转所形成的角.
③零角:如果一条射线没有做任何旋转,我们称它形成了一个零角.
3、角的运算
设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是任意两个角， SKIPIF 1 < 0 为角 SKIPIF 1 < 0 的相反角．
(1) SKIPIF 1 < 0 ：把角 SKIPIF 1 < 0 的终边旋转角 SKIPIF 1 < 0 .（ SKIPIF 1 < 0 时,旋转量为 SKIPIF 1 < 0 ,按逆时针方向旋转; SKIPIF 1 < 0 时,旋转量为 SKIPIF 1 < 0 ,按顺时针方向旋转）
(2) SKIPIF 1 < 0 ： SKIPIF 1 < 0
【即学即练1】（2023秋·高一课时练习）若角α＝30°，把角α逆时针旋转20°得到角β，则β＝ .
【答案】50°
【详解】因为由 SKIPIF 1 < 0 逆时针旋转得到 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
知识点02：象限角
1、定义：在直角坐标系中,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.那么,角的终边在第几象限,就说这个角是第几象限角.
如果角的终边在坐标轴上,那么就认为这个角不属于任何一个象限.
2、象限角的常用表示：
知识点03：轴线角
1、定义：轴线角是指以原点为顶点， SKIPIF 1 < 0 轴非负半轴为始边，终边落在坐标轴上的角.
2、轴线角的表示：
知识点04：终边相同的角的集合
所有与角 SKIPIF 1 < 0 终边相同的角为 SKIPIF 1 < 0
【即学即练2】下列各角中，与 SKIPIF 1 < 0 角终边重合的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】与 SKIPIF 1 < 0 角终边重合的角为： SKIPIF 1 < 0 ，则当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，故C正确.
经检验，其他选项都不正确.故选：C.
知识点05：角度制与弧度制的概念
1、弧度制
长度等于半径长的圆弧所对的圆心角叫做1弧度角，记作1 SKIPIF 1 < 0 ，或1弧度，或1(单位可以省略不写).
2、角度与弧度的换算
弧度与角度互换公式： SKIPIF 1 < 0 SKIPIF 1 < 0 ， SKIPIF 1 < 0
3、常用的角度与弧度对应表
【即学即练3】利用单位圆，写出 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 的圆心角的弧度数．
【答案】 SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0 ； SKIPIF 1 < 0
【详解】在单位圆中， SKIPIF 1 < 0 的圆心角的弧长是 SKIPIF 1 < 0 ，那么它对应的弧度数是 SKIPIF 1 < 0 ；
SKIPIF 1 < 0 的圆心角的弧长是 SKIPIF 1 < 0 ，那么它对应的弧度数是 SKIPIF 1 < 0 ；
SKIPIF 1 < 0 的圆心角对应的弧度数是 SKIPIF 1 < 0 ； SKIPIF 1 < 0 的圆心角对应的弧度数是 SKIPIF 1 < 0 ．
知识点06：扇形中的弧长公式和面积公式
弧长公式： SKIPIF 1 < 0 ( SKIPIF 1 < 0 是圆心角的弧度数)，
扇形面积公式： SKIPIF 1 < 0 .
【即学即练4】已知一扇形的圆心角为 SKIPIF 1 < 0 ，半径为9，则该扇形的面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【详解】因为 SKIPIF 1 < 0 ，所以该扇形的面积为 SKIPIF 1 < 0 ．故选：A
题型01任意角的概念
【典例1】（多选）钟表在我们的生活中随处可见，高一某班的同学们在学习了“任意角和弧度制”后，对钟表的运行产生了浓厚的兴趣，并展开了激烈的讨论，若将时针与分针视为两条线段，则下列说法正确的是（ ）
A．小赵同学说：“经过了5 h，时针转了 SKIPIF 1 < 0 ．”
B．小钱同学说：“经过了40 min，分针转了 SKIPIF 1 < 0 ．”
C．小孙同学说：“当时钟显示的时刻为12:35时，时针与分针所夹的钝角为 SKIPIF 1 < 0 ．”
D．小李同学说：“时钟的时针与分针一天之内会重合22次．”
【答案】ACD
【详解】解：经过了5 h，时针转过的角度对应的弧度数为 SKIPIF 1 < 0 ，故A正确．
经过了40 min，分针转过的角度对应的弧度数为 SKIPIF 1 < 0 ，故B错误．
时钟显示的时刻为12:35，该时刻的时针与分针所夹的钝角为 SKIPIF 1 < 0 ，故C正确．
分针比时针多走一圈便会重合一次，设分针走了t min，第n次和时针重合，则 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，故D正确．故选：ACD
【典例2】亲爱的考生，我们数学考试完整的时间是2小时，则从考试开始到结束，钟表的分针转过的弧度数为 .
【答案】 SKIPIF 1 < 0
【详解】因为钟表的分针转了两圈，且是按顺时针方向旋转，所以钟表的分针转过的弧度数为 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
【变式1】经过2个小时，钟表的时针和分针转过的角度分别是（ ）.
A．60°，720°B．－60°，－720°
C．－30°，－360°D．－60°，720°
【答案】B
【详解】钟表的时针和分针都是顺时针旋转，因此转过的角度都是负的，而 SKIPIF 1 < 0 ×360°＝60°，2×360°＝720°，
故钟表的时针和分针转过的角度分别是－60°，－720°.故选：B
【变式2】时钟走了3小时20分，则时针所转过的角的度数为 ，分针转过的角的度数为 ．
【答案】 SKIPIF 1 < 0 SKIPIF 1 < 0
【详解】因为时针每小时转 SKIPIF 1 < 0 ，分针每小时转 SKIPIF 1 < 0 ，又因为时针、分针都按顺时针方向旋转，
故时针转过的角度数为 SKIPIF 1 < 0 ，分针转过的角度数为 SKIPIF 1 < 0 ．
故答案为： SKIPIF 1 < 0 ； SKIPIF 1 < 0
题型02终边相同的角
【典例1】下列各角中，与 SKIPIF 1 < 0 角终边相同的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】对于B，因为 SKIPIF 1 < 0 ，所以角 SKIPIF 1 < 0 与角 SKIPIF 1 < 0 的终边相同，B正确；
对于A，因为 SKIPIF 1 < 0 不是 SKIPIF 1 < 0 的整数倍，所以它们的终边不同，A错误；
对于C，因为 SKIPIF 1 < 0 不是 SKIPIF 1 < 0 的整数倍，所以它们的终边不同，C错误；
对于D，因为 SKIPIF 1 < 0 不是 SKIPIF 1 < 0 的整数倍，所以它们的终边不同，D错误.故选：B.
【典例2】（多选）与 SKIPIF 1 < 0 角终边相同的角的集合是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】AC
【详解】与 SKIPIF 1 < 0 终边相同的角可写为： SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 与 SKIPIF 1 < 0 角终边相同的角的集合为： SKIPIF 1 < 0 ，A正确； SKIPIF 1 < 0 ，C正确.故选：AC.
【变式1】下列角的终边与 SKIPIF 1 < 0 角的终边关于 SKIPIF 1 < 0 轴对称的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【详解】由题意知，与 SKIPIF 1 < 0 角的终边关于 SKIPIF 1 < 0 轴对称的角为 SKIPIF 1 < 0
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 正确.经验证，其他三项均不符合要求.故选： SKIPIF 1 < 0 .
【变式2】已知﹣990°＜α＜﹣630°，且α与120°角终边相同，则α= ．
【答案】﹣960°．
【详解】试题分析：α与120°角终边相同，可表示为α=k•360°+120°，k∈Z，结合角的范围，可得结论．
解：α与120°角终边相同，∴α=k•360°+120°，k∈Z．
∵﹣990°＜k•360°+120°＜﹣630°，∴﹣1110°＜k•360°＜﹣750°．又k∈Z，
∴k=﹣3，此时α=（﹣3）×360°+120°=﹣960°．故答案为﹣960°．
题型03终边在某条直线上的角的集合
【典例1】若角 SKIPIF 1 < 0 的终边在函数 SKIPIF 1 < 0 的图象上，试写出角 SKIPIF 1 < 0 的集合为 ．
【答案】 SKIPIF 1 < 0
【详解】解：函数 SKIPIF 1 < 0 的图象是第二、四象限的平分线，在 SKIPIF 1 < 0 ～ SKIPIF 1 < 0 范围内，以第二象限射线为终边的角为 SKIPIF 1 < 0 ，以第四象限射线为终边的角为 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 的集合为 SKIPIF 1 < 0 或 SKIPIF 1 < 0 SKIPIF 1 < 0 ．故答案为： SKIPIF 1 < 0 ．
【典例2】写出终边在如图所示的直线上的角的集合．

【答案】答案见解析
【详解】（1）在0°～360°范围内，终边在直线y＝0上的角有两个，即0°和180°，
又所有与0°角终边相同的角的集合为 SKIPIF 1 < 0 ，
所有与180°角终边相同的角的集合为 SKIPIF 1 < 0 ，
于是，终边在直线y＝0上的角的集合为 SKIPIF 1 < 0 ．
（2）由图形易知，在0°～360°范围内，终边在直线y＝－x上的角有两个，即135°和315°，
因此，终边在直线y＝－x上的角的集合为 SKIPIF 1 < 0 ．
（3）结合（2）知所求角的集合为 SKIPIF 1 < 0
同理可得终边在直线y＝x、y=-x上的角的集合为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
【变式1】若角α的顶点为坐标原点，始边在x轴的非负半轴上，终边在直线 SKIPIF 1 < 0 上，则角α的取值集合是
【答案】 SKIPIF 1 < 0
【详解】直线 SKIPIF 1 < 0 的倾斜角是 SKIPIF 1 < 0 ，所以终边落在直线 SKIPIF 1 < 0 上的角的取值集合为 SKIPIF 1 < 0 故答案为： SKIPIF 1 < 0
【变式2】在直角坐标系中写出下列角的集合：
(1)终边在 SKIPIF 1 < 0 轴的非负半轴上；
(2)终边在 SKIPIF 1 < 0 上．
【答案】(1) SKIPIF 1 < 0 ；(2) SKIPIF 1 < 0 .
【详解】（1）在0°～360°范围内，终边在x轴的非负半轴上的角有一个，它是0°，
所以终边落在x轴的非负半轴上的角的集合为 SKIPIF 1 < 0 .
（2）在0°～360°范围内，终边在y=x(x≥0)上的角有一个，它是45°，
所以终边在y=x(x≥0)上的角的集合为 SKIPIF 1 < 0 .
题型04 区域角
【典例1】用弧度分别表示终边落在如图（1）（2）所示的阴影部分内（不包括边界）的角的集合．（如无特别说明，边界线为实线代表包括边界，边界线为虚线代表不包括边界）

【答案】图1 SKIPIF 1 < 0 ；图2 SKIPIF 1 < 0
【详解】（1） SKIPIF 1 < 0 角的终边可以看作是 SKIPIF 1 < 0 角的终边，化为弧度，即 SKIPIF 1 < 0 ， SKIPIF 1 < 0 角的终边即 SKIPIF 1 < 0 的终边，
所以终边落在阴影部分内（不包括边界）的角的集合为 SKIPIF 1 < 0 ．
（2）与（1）类似可写出终边落在阴影部分内（不包括边界）的角的集合为 SKIPIF 1 < 0 SKIPIF 1 < 0 ．
【典例2】写出终边落在图中阴影区域内的角的集合．
(1) (2)
【答案】(1) SKIPIF 1 < 0 (2) SKIPIF 1 < 0
【详解】（1）在 SKIPIF 1 < 0 范围内，图中终边在第二象限的区域边界线所对应的角为 SKIPIF 1 < 0 ，终边在第四象限的区域边界线所对应的角为 SKIPIF 1 < 0 ，
因此，阴影部分区域所表示的集合为 SKIPIF 1 < 0 ；
（2）图中从第四象限到第一象限阴影部分区域表示的角的集合为 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
图中从第二象限到第三象限阴影部分区域所表示的角的集合为
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
因此，阴影部分区域所表示角的集合为
SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 .
【变式1】）集合 SKIPIF 1 < 0 中的角所表示的范围(阴影部分)是（ ）
A． B． C． D．
【答案】C
【详解】当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 表示的范围与 SKIPIF 1 < 0 表示的范围一样；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 表示的范围与 SKIPIF 1 < 0 表示的范围一样，故选：C．
【变式2】已知角 SKIPIF 1 < 0 的终边在如图所示的阴影区域内，则角 SKIPIF 1 < 0 的取值范围是 ．
【答案】 SKIPIF 1 < 0
【详解】终边在 SKIPIF 1 < 0 角的终边所在直线上的角的集合为 SKIPIF 1 < 0 ，
终边在 SKIPIF 1 < 0 角的终边所在直线上的角的集合为 SKIPIF 1 < 0 ，
因此终边在题图中的阴影区域内的角 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 ，
所以角 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 ，
故答案为： SKIPIF 1 < 0
【变式3】用弧度表示终边落在如图所示的阴影部分内（不包括边界）的角的集合.

【答案】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0
【详解】（1） SKIPIF 1 < 0 ；
（2） SKIPIF 1 < 0 SKIPIF 1 < 0 .
题型05确定角的终边所在的象限
【典例1】已知 SKIPIF 1 < 0 为第二象限角，则 SKIPIF 1 < 0 所在的象限是（ ）
A．第一或第二象限B．第二或第三象限
C．第二或第四象限D．第一或第三象限
【答案】D
【详解】因为 SKIPIF 1 < 0 为第二象限角，则 SKIPIF 1 < 0 ，
所以， SKIPIF 1 < 0 ，
①当 SKIPIF 1 < 0 为奇数时，设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 为第三象限角；
②当 SKIPIF 1 < 0 为偶数时，设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
此时 SKIPIF 1 < 0 为第一象限角.综上所述， SKIPIF 1 < 0 为第一或第三象限角.故选：D.
【典例2】（多选）如果α是第三象限的角，那么 SKIPIF 1 < 0 可能是下列哪个象限的角（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】ACD
【详解】 SKIPIF 1 < 0 是第三象限的角，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，在第一象限；
当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，在第三象限；
当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，在第四象限；
所以 SKIPIF 1 < 0 可以是第一、第三、或第四象限角．故选：ACD
【典例3】已知角 SKIPIF 1 < 0 第二象限角，且 SKIPIF 1 < 0 ，则角 SKIPIF 1 < 0 是（ ）
A．第一象限角B．第二象限角
C．第三象限角D．第四象限角
【答案】C
【详解】因为角 SKIPIF 1 < 0 第二象限角，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 是偶数时，设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 为第一象限角；
当 SKIPIF 1 < 0 是奇数时，设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 为第三象限角.；
综上所述： SKIPIF 1 < 0 为第一象限角或第三象限角，因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 为第三象限角．
故选：C．
【变式1】已知 SKIPIF 1 < 0 是第一象限角，那么（ ）
A． SKIPIF 1 < 0 是第一、二象限角B． SKIPIF 1 < 0 是第一、三象限角
C． SKIPIF 1 < 0 是第三、四象限角D． SKIPIF 1 < 0 是第二、四象限角
【答案】B
【详解】因为 SKIPIF 1 < 0 是第一象限角，所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 为偶数时， SKIPIF 1 < 0 是第一象限角，当 SKIPIF 1 < 0 为奇数时， SKIPIF 1 < 0 是第三象限角，综上所述， SKIPIF 1 < 0 第一、三象限角.
故选：B.
【变式2】若 SKIPIF 1 < 0 是第三象限角，则 SKIPIF 1 < 0 所在的象限是（ ）
A．第一或第二象限；B．第三或第四象限；
C．第一或第三象限；D．第二或第四象限．
【答案】D
【详解】因为 SKIPIF 1 < 0 为第三象限角, 即 SKIPIF 1 < 0 ,所以, SKIPIF 1 < 0 ,
当 SKIPIF 1 < 0 为奇数时, SKIPIF 1 < 0 是第四象限的角;当 SKIPIF 1 < 0 为偶数时, SKIPIF 1 < 0 是第二象限的角.故选:D.
【变式3】若角 SKIPIF 1 < 0 是第二象限角，试确定角 SKIPIF 1 < 0 ， SKIPIF 1 < 0 是第几象限角．
【答案】 SKIPIF 1 < 0 可能是第三象限角、第四象限角或终边在 SKIPIF 1 < 0 轴非正半轴上的角； SKIPIF 1 < 0 可能是第一象限角、第二象限角或第四象限角
【详解】因为 SKIPIF 1 < 0 是第二象限角，所以 SKIPIF 1 < 0 ，
可得 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 可能是第三象限角、第四象限角或终边在 SKIPIF 1 < 0 轴非正半轴上的角．
又由 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 是第一象限角；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 是第二象限角；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 是第四象限角．
综上所述， SKIPIF 1 < 0 可能是第一象限角、第二象限角或第四象限角．
题型06弧度制的概念
【典例1】自行车的大链轮有88齿，小链轮有20齿，当大链轮逆时针转过一周时，小链轮转过的弧度数是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】由题意，当大链轮逆时针转过一周时，小链轮逆时针转过 SKIPIF 1 < 0 周，小链轮转过的弧度是 SKIPIF 1 < 0 .故选B.
【典例2】下列说法正确的是（ ）
A．弧度的圆心角所对的弧长等于半径
B．大圆中弧度的圆心角比小圆中弧度的圆心角大
C．所有圆心角为弧度的角所对的弧长都相等
D．用弧度表示的角都是正角
【答案】A
【详解】对于A，根据弧度的定义知，“1弧度的圆心角所对的弧长等于半径”，故A正确；对于B，大圆中1弧度的圆心角与小圆中1弧度的圆心角相等，故B错误；对于C，不在同圆或等圆中，1弧度的圆心角所对的弧长是不等的，故C错误；对于D，用弧度表示的角也可以不是正角，故D错误．
【变式1】下列与 SKIPIF 1 < 0 终边相同角的集合中正确的是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】因为角度值和弧度制不能混用，故A、B错误；因为 SKIPIF 1 < 0 ，故C正确；
对于选项D：因为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 与 SKIPIF 1 < 0 终边不相同，故D错误；
故选：C.
【变式2】若 SKIPIF 1 < 0 ，则角 SKIPIF 1 < 0 的终边在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】A
【详解】由于 SKIPIF 1 < 0 ，故角 SKIPIF 1 < 0 的终边在第一象限，故选：A
题型07角度与弧度的互化
【典例1】（多选）下列各角中，与角 SKIPIF 1 < 0 终边相同的角为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】AB
【详解】对于A， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，故A正确；对于B，与 SKIPIF 1 < 0 终边相同的角为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，故B正确；对于C，令 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，故C错误；对于D，令 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，故D错误．故选：AB.
【典例2】把下列各角从度化为弧度：(1) SKIPIF 1 < 0 ； (2) SKIPIF 1 < 0 ．
【答案】(1) SKIPIF 1 < 0 (2) SKIPIF 1 < 0
【详解】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ．
【变式1】设r为圆的半径，弧长为 SKIPIF 1 < 0 的圆弧所对的圆心角为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【详解】由弧长、圆心角、半径的关系： SKIPIF 1 < 0 ，
弧长为 SKIPIF 1 < 0 的圆弧所对的圆心角： SKIPIF 1 < 0 .故选：A.
【变式2】 SKIPIF 1 < 0 化为角度是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】 SKIPIF 1 < 0 .故选：B
题型08用弧度表示角或范围
【典例1】写出一个与角 SKIPIF 1 < 0 终边相同的正角： SKIPIF 1 < 0 （用弧度数表示）.
【答案】 SKIPIF 1 < 0 （答案不唯一，符合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 即可）
【详解】与角 SKIPIF 1 < 0 终边相同的角： SKIPIF 1 < 0
又题目要求正角， SKIPIF 1 < 0 可取 SKIPIF 1 < 0 ，化为弧度数为 SKIPIF 1 < 0 .答案不唯一
故答案为： SKIPIF 1 < 0 （答案不唯一，符合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 即可）
【典例2】已知 SKIPIF 1 < 0 .
(1)将 SKIPIF 1 < 0 写成 SKIPIF 1 < 0 的形式，并指出它是第几象限角；
(2)求与 SKIPIF 1 < 0 终边相同的角 SKIPIF 1 < 0 ，满足 SKIPIF 1 < 0 ．
【答案】(1) SKIPIF 1 < 0 ，是第四象限角；(2) SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
【详解】（1）因为 SKIPIF 1 < 0 , SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 是第四象限角.
（2） SKIPIF 1 < 0 ，
所以与 SKIPIF 1 < 0 终边相同的角可表示为 SKIPIF 1 < 0 ,
令 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .所以 SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
【变式1】将－1485°化成 SKIPIF 1 < 0 的形式是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【详解】因为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，所以－1485°可化成 SKIPIF 1 < 0 ．
故选：D．
【变式2】已知角 SKIPIF 1 < 0 .
(1)将 SKIPIF 1 < 0 改写成 SKIPIF 1 < 0 的形式，并指出 SKIPIF 1 < 0 是第几象限的角；
(2)在区间 SKIPIF 1 < 0 上找出与 SKIPIF 1 < 0 终边相同的角．
【答案】(1) SKIPIF 1 < 0 ，第二象限角(2) SKIPIF 1 < 0 和 SKIPIF 1 < 0
【详解】（1） SKIPIF 1 < 0 ，因为 SKIPIF 1 < 0 为第二象限，所以 SKIPIF 1 < 0 是第二象限角；
（2）与 SKIPIF 1 < 0 终边相同的角可以写出 SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 ，得当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，所以在区间 SKIPIF 1 < 0 上与 SKIPIF 1 < 0 终边相同的角为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ．
题型09弧长公式
【典例1】若扇形的面积是 SKIPIF 1 < 0 ，它的周长是 SKIPIF 1 < 0 ，则扇形圆心角（正角）的弧度数为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【详解】设扇形的半径为 SKIPIF 1 < 0 ，圆心角为 SKIPIF 1 < 0 ，由题意，得 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 得， SKIPIF 1 < 0 ，代入 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 （舍去）．
故扇形圆心角的弧度数为 SKIPIF 1 < 0 ．故选：A
【典例2】若扇形的圆心角为 SKIPIF 1 < 0 ，半径 SKIPIF 1 < 0 .则它的弧长为 .
【答案】 SKIPIF 1 < 0
【详解】因为 SKIPIF 1 < 0 ，又扇形的圆心角为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，所以它的弧长为 SKIPIF 1 < 0 ，故答案为： SKIPIF 1 < 0
【变式1】已知扇形面积 SKIPIF 1 < 0 ，半径是1，则扇形的周长是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】设扇形的弧长为 SKIPIF 1 < 0 ，由扇形的面积公式可得， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
则扇形的周长为 SKIPIF 1 < 0 .故选：C
【变式2】已知扇形的面积为2，扇形圆心角的弧度数是2，则扇形的周长为 .
【答案】 SKIPIF 1 < 0
【详解】设扇形的半径为 SKIPIF 1 < 0 ，由题意可得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
所以扇形的周长为 SKIPIF 1 < 0 .故答案为： SKIPIF 1 < 0 .
题型10扇形面积公式
【典例1】圆心角为2的扇形的周长为4，则此扇形的面积为 .
【答案】1
【详解】设扇形的半径为 SKIPIF 1 < 0 ，弧长为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，扇形的面积 SKIPIF 1 < 0 .
故答案为：1.
【典例2】建于明朝的杜氏雕花楼被誉为“松江最美的一座楼”，该建筑内有很多精美的砖雕，砖雕是我国古建筑雕刻中很重要的一种艺术形式，传统砖墙精致细腻、气韵生动、极富书卷气．如图是一扇环形砖雕，可视为扇形OCD截去同心扇形OAB所得部分，已知 SKIPIF 1 < 0 ，弧 SKIPIF 1 < 0 ，弧 SKIPIF 1 < 0 ，则此扇环形砖雕的面积为 SKIPIF 1 < 0 ．

【答案】 SKIPIF 1 < 0
【详解】设圆心角为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以此扇环形砖雕的面积为 SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 .故答案为： SKIPIF 1 < 0
【变式1】已知扇形弧长为 SKIPIF 1 < 0 ，圆心角为2，则该扇形面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．1
【答案】B
【详解】设扇形所在圆的半径为 SKIPIF 1 < 0 ，因为扇形弧长为 SKIPIF 1 < 0 ，圆心角为 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，
由扇形的面积公式，可得 SKIPIF 1 < 0 .故选：B.
【变式2】工艺扇面是中国书画的一种常见表现形式.某班级想用布料制作一面如图所示的扇面，已知扇面展开的中心角为 SKIPIF 1 < 0 ，外圆半径为40cm，内圆半径为20cm，那么制作这样一面扇面至少需要用布料为 cm2

【答案】400π
【详解】解：根据题意，由扇形的面积公式可得：
制作这样一面扇面需要的布料为 SKIPIF 1 < 0 .
故答案为：400π
题型11扇形中的最值问题
【典例1】已知一个扇形的周长为8，则当该扇形的面积取得最大值时，圆心角大小为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．2
【答案】D
【详解】设扇形的半径为 SKIPIF 1 < 0 ，弧长为 SKIPIF 1 < 0 ，由已知得 SKIPIF 1 < 0 ，
扇形面积为 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时等号成立，此时 SKIPIF 1 < 0 ，则圆心角 SKIPIF 1 < 0 ，故选：D.
【典例2】已知一扇形的圆心角为 SKIPIF 1 < 0 ，半径为R，弧长为l．
(1)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求扇形的弧长l；
(2)若扇形面积为16，求扇形周长的最小值，及此时扇形的圆心角 SKIPIF 1 < 0 ．
【答案】(1) SKIPIF 1 < 0 (2)扇形周长的最小值为 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0
【详解】（1）因为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，所以扇形的弧长 SKIPIF 1 < 0 ；
（2）由扇形面积 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，则扇形周长为 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时，取等号，此时， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以扇形周长的最小值为 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 .
【典例3】已知扇形的圆心角是 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 .
（1）若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 求扇形的弧长 SKIPIF 1 < 0 .
（2）若扇形的周长为 SKIPIF 1 < 0 ，当扇形的圆心角 SKIPIF 1 < 0 为多少弧度时，这个扇形的面积最大？最大面积是多少？
【答案】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ，扇形的面积取得最大值25.
【详解】解：（1） SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
（2）由已知得， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得最大值25，此时 SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
【变式1】已知扇形的圆心角为 SKIPIF 1 < 0 ，所在圆的半径为 SKIPIF 1 < 0
(1)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求扇形的弧长 SKIPIF 1 < 0
(2)若扇形的周长为 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 为多少弧度时，该扇形面积最大 SKIPIF 1 < 0 并求出最大面积．
【答案】(1) SKIPIF 1 < 0 (2)当 SKIPIF 1 < 0 时，扇形的面积最大，最大面积是 SKIPIF 1 < 0 ．
【详解】（1）设扇形的弧长为 SKIPIF 1 < 0 ． SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ， SKIPIF 1 < 0 SKIPIF 1 < 0 .
（2）由题设条件知， SKIPIF 1 < 0 ,
因此扇形的面积 SKIPIF 1 < 0
SKIPIF 1 < 0 当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 有最大值 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 ,
SKIPIF 1 < 0 当 SKIPIF 1 < 0 时，扇形的面积最大，最大面积是 SKIPIF 1 < 0 ．
【变式1】已知扇形的圆心角为 SKIPIF 1 < 0 ，所在圆的半径为r．
(1)若 SKIPIF 1 < 0 ，求扇形的弧长．
(2)若扇形的周长为24，当 SKIPIF 1 < 0 为多少弧度时，该扇形面积最大？求出最大面积．
【答案】(1) SKIPIF 1 < 0 (2) SKIPIF 1 < 0
【详解】（1）设扇形的弧长为l．因为 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ．
（2）由题设条件，知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
所以扇形的面积 SKIPIF 1 < 0 ．当 SKIPIF 1 < 0 时，S有最大值36，
此时 SKIPIF 1 < 0 ，所以当 SKIPIF 1 < 0 时，扇形的面积最大，最大面积是36．
【变式1】已知一扇形的圆心角为 SKIPIF 1 < 0 ，所在圆的半径为R.
（1）若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求扇形的弧长及该弧所在的弓形的面积；
（2）若扇形的周长为20 cm，当扇形的圆心角 SKIPIF 1 < 0 等于多少弧度时，这个扇形的面积最大?
【答案】（1） SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 .
【详解】（1）设扇形的弧长为l，弓形面积为S，则
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
（2）设扇形弧长为l，则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
∴扇形面积 SKIPIF 1 < 0 ，
∴当 SKIPIF 1 < 0 时，S有最大值 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
因此当 SKIPIF 1 < 0 时，这个扇形面积最大.
A夯实基础
一、单选题
1．下列说法中正确的是（ ）
A．锐角是第一象限角B．终边相等的角必相等
C．小于 SKIPIF 1 < 0 的角一定在第一象限D．第二象限角必大于第一象限角
【答案】A
【详解】锐角是指大于 SKIPIF 1 < 0 小于 SKIPIF 1 < 0 的角，故其在第一象限，即A正确；
选项B．终边相等的角必相等，两角可以相差 SKIPIF 1 < 0 整数倍，故错误；
选项C．小于 SKIPIF 1 < 0 的角不一定在第一象限，也可以为负角，故错误；
选项D．根据任意角的定义，第二象限角可以为负角，第一象限角可以为正角，此时第二象限角小于第一象限角，故错误.故选：A
2．把 SKIPIF 1 < 0 表示成 SKIPIF 1 < 0 的形式，则θ的值可以是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】B
【详解】∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，故选：B．
3．已知角的集合 SKIPIF 1 < 0 ，则在 SKIPIF 1 < 0 内的角有（ ）
A．2个B．3个C．4个D．5个
【答案】B
【详解】依题意，解不等式 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 ，因此 SKIPIF 1 < 0 ，
所以在 SKIPIF 1 < 0 内的角有3个.故选：B
4．一只红蚂蚁与一只黑蚂蚁在一个圆（半径为1cm）的圆周上爬动，且两只蚂蚁均从点 SKIPIF 1 < 0 同时逆时针匀速爬动，红蚂蚁以 SKIPIF 1 < 0 的速度爬行，黑蚂蚁以 SKIPIF 1 < 0 的速度爬行，则2秒钟后，两只蚂蚁之间的直线距离为（ ）
A．1B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【详解】
如图所示，红蚂蚁以 SKIPIF 1 < 0 的速度爬行，黑蚂蚁以 SKIPIF 1 < 0 的速度爬行，
则2秒钟后，红蚂蚁绕圆的角度为 SKIPIF 1 < 0 ，到达B处，黑蚂蚁绕圆的角度为 SKIPIF 1 < 0 ，到达C处，
此时 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 为正三角形，故 SKIPIF 1 < 0 .故选：A
5．已知集合 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【详解】当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 .故选：A
6．某圆台的侧面展开图为如图所示的扇环（实线部分），已知该扇环的面积为 SKIPIF 1 < 0 ，两段圆弧所在圆的半径分别为1和2，则扇环的圆心角 SKIPIF 1 < 0 的大小为（ ）

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】D
【详解】由该扇环的面积为 SKIPIF 1 < 0 ，两段圆弧所在圆的半径分别为1和2，
可得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，即扇环的圆心角 SKIPIF 1 < 0 的大小为 SKIPIF 1 < 0 .故选：D.
7．扇面书画在中国传统绘画中由来已久，最早关于扇面书画的文献记载，是《王羲之书六角扇》.扇面书画发展到明清时期，折扇扇面画开始逐渐地成为主流，如图，该折扇扇面画的外弧长为48，内弧长为28，且该扇面所在扇形的圆心角约为120°，则该扇面画的面积约为（ ）（参考数据： SKIPIF 1 < 0 ）

A．990B．495C．380D．300
【答案】C
【详解】如图，

设该扇面画的外弧所在圆的半径为R，弧长为 SKIPIF 1 < 0 ，内弧所在圆的半径为r，弧长为 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，所以扇面画的面积约为 SKIPIF 1 < 0 .故选：C.
8．玉雕在我国历史悠久，玉雕是采用传统的手工雕刻工艺加工生产成的玉雕工艺.某扇环形玉雕（扇环是一个圆环被扇形截得的一部分）尺寸（单位：cm）如图所示，则该玉雕的面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】A
【详解】如图，设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，由弧长公式可得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
设扇形 SKIPIF 1 < 0 ，扇形 SKIPIF 1 < 0 的面积分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则该壁画的扇面面积约为 SKIPIF 1 < 0 ．故选：A
二、多选题
9．若角 SKIPIF 1 < 0 的终边与角 SKIPIF 1 < 0 的终边关于 SKIPIF 1 < 0 轴对称，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值可能为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】AD
【详解】因为角 SKIPIF 1 < 0 的终边与角 SKIPIF 1 < 0 的终边关于x轴对称，所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
又因为 SKIPIF 1 < 0 ，所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .故选：AD.
10．已知 SKIPIF 1 < 0 为第四象限角，则 SKIPIF 1 < 0 可能为（ ）
A．第一象限角B．第二象限角
C．第三象限角D．第四象限角
【答案】BCD
【详解】由题意知 SKIPIF 1 < 0 为第四象限角，则 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为第四象限角，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为第二象限角，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为第三象限角，
即 SKIPIF 1 < 0 可能为第二、三、四象限角，不可能为第一象限角，故选： SKIPIF 1 < 0
三、填空题
11．已知半径为 SKIPIF 1 < 0 的扇形的圆心角为 SKIPIF 1 < 0 ，则扇形的面积为 ．
【答案】 SKIPIF 1 < 0
【详解】因为半径 SKIPIF 1 < 0 扇形的圆心角为 SKIPIF 1 < 0 ，则圆心角 SKIPIF 1 < 0 ，所以弧长 SKIPIF 1 < 0 ，面积 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
12．如图，半径为1的圆M与直线l相切于点A，圆M沿着直线l滚动．当圆M滚动到圆 SKIPIF 1 < 0 时，圆 SKIPIF 1 < 0 与直线l相切于点B，点A运动到点 SKIPIF 1 < 0 ，线段AB的长度为 SKIPIF 1 < 0 ，则点 SKIPIF 1 < 0 到直线 SKIPIF 1 < 0 的距离为 ．
【答案】 SKIPIF 1 < 0 / SKIPIF 1 < 0
【详解】根据条件可知圆周长为 SKIPIF 1 < 0 ，∵ SKIPIF 1 < 0 ，故可得圆旋转了 SKIPIF 1 < 0 圆周， SKIPIF 1 < 0 位置如图：
则 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 是等腰直角三角形，则 SKIPIF 1 < 0 到 SKIPIF 1 < 0 的距离 SKIPIF 1 < 0 ，
故答案为： SKIPIF 1 < 0 ．
四、解答题
13．写出终边在下图所示的直线上的角的集合．

【答案】（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0
【详解】（1）由题图易知，在 SKIPIF 1 < 0 范围内，终边在直线 SKIPIF 1 < 0 上的角有两个，即 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，
因此，终边在直线 SKIPIF 1 < 0 上的角的集合为
SKIPIF 1 < 0
SKIPIF 1 < 0 SKIPIF 1 < 0 ；
（2）同理可得终边在直线 SKIPIF 1 < 0 上的角的集合为
SKIPIF 1 < 0 ，
终边在直线 SKIPIF 1 < 0 上的角的集合为 SKIPIF 1 < 0
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
所以终边在直线 SKIPIF 1 < 0 上和在直线 SKIPIF 1 < 0 上的角的集合为
SKIPIF 1 < 0 SKIPIF 1 < 0 .
14．已知一扇形的圆心角为 SKIPIF 1 < 0 ，周长为 SKIPIF 1 < 0 ，面积为 SKIPIF 1 < 0 ，弧长为 SKIPIF 1 < 0 ,所在圆的半径为 SKIPIF 1 < 0 ．
(1)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求扇形的弧长；
(2)若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求扇形的半径和圆心角．
【答案】(1) SKIPIF 1 < 0 (2)扇形半径为4，圆心角为 SKIPIF 1 < 0
【详解】（1）由已知得 SKIPIF 1 < 0 ；
（2）由已知得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
即扇形的半径为4，圆心角为 SKIPIF 1 < 0 .
B能力提升
1．古希腊地理学家埃拉托色尼从书中得知，位于尼罗河第一瀑布的塞伊尼（现在的阿斯旺，在北回归线上）记为 SKIPIF 1 < 0 ，夏至那天正午，阳光直射，立杆无影；同样在夏至那天，他所在的城市——埃及北部的亚历山大城记为 SKIPIF 1 < 0 ，测得立杆与太阳光线所成的角约为 SKIPIF 1 < 0 .他又派人测得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 两地的距离 SKIPIF 1 < 0 km，平面示意图如图，则可估算地球的半径约为（ ）（ SKIPIF 1 < 0 ）
A． SKIPIF 1 < 0 kmB． SKIPIF 1 < 0 kmC． SKIPIF 1 < 0 kmD． SKIPIF 1 < 0 km
【答案】C
【详解】设地心为 SKIPIF 1 < 0 ，依题意可得， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，设地球的周长为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 km.故选：C
2．数学中处处存在着美，莱洛三角形就给人以对称的美感.莱洛三角形的画法如下：先画等边三角形 SKIPIF 1 < 0 ，再分别以点 SKIPIF 1 < 0 为圆心，线段 SKIPIF 1 < 0 长为半径画圆弧，便得到莱洛三角形（如图所示）.若莱洛三角形的周长为 SKIPIF 1 < 0 ，则其面积是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【答案】C
【详解】莱洛三角形的周长为 SKIPIF 1 < 0 ，可得弧长 SKIPIF 1 < 0 ，则等边三角形的边长 SKIPIF 1 < 0 ，
分别以点A、B、C为圆心，圆弧 SKIPIF 1 < 0 所对的扇形面积均为 SKIPIF 1 < 0 ，
等边 SKIPIF 1 < 0 的面积 SKIPIF 1 < 0 ，所以莱洛三角形的面积是 SKIPIF 1 < 0 .故选：C.
3．（多选）已知三角形 SKIPIF 1 < 0 是边长为 SKIPIF 1 < 0 的等边三角形.如图，将三角形 SKIPIF 1 < 0 的顶点 SKIPIF 1 < 0 与原点重合. SKIPIF 1 < 0 在 SKIPIF 1 < 0 轴上，然后将三角形沿着 SKIPIF 1 < 0 轴顺时针滚动，每当顶点 SKIPIF 1 < 0 再次回落到 SKIPIF 1 < 0 轴上时，将相邻两个 SKIPIF 1 < 0 之间的距离称为“一个周期”，给出以下四个结论，其中说法正确的是（ ）
A．一个周期是 SKIPIF 1 < 0
B．完成一个周期，顶点 SKIPIF 1 < 0 的轨迹是一个半圆
C．完成一个周期，顶点 SKIPIF 1 < 0 的轨迹长度是 SKIPIF 1 < 0
D．完成一个周期，顶点 SKIPIF 1 < 0 的轨迹与 SKIPIF 1 < 0 轴围成的面积是 SKIPIF 1 < 0
【答案】ACD
【详解】由已知可得：点 SKIPIF 1 < 0 一个周期的运动轨迹如图所示，
对于A，当 SKIPIF 1 < 0 再次回落到 SKIPIF 1 < 0 轴上时，发生了 SKIPIF 1 < 0 个单位的位移，则一个周期为 SKIPIF 1 < 0 ，A正确；
对于B，完成一个周期，顶点 SKIPIF 1 < 0 的轨迹由以 SKIPIF 1 < 0 为圆心， SKIPIF 1 < 0 为半径的 SKIPIF 1 < 0 圆和以 SKIPIF 1 < 0 为圆心， SKIPIF 1 < 0 为半径的 SKIPIF 1 < 0 圆共同组成，不是一个半圆，B错误；
对于C，由B知，顶点 SKIPIF 1 < 0 的轨迹为 SKIPIF 1 < 0 ，C正确；
对于D，顶点 SKIPIF 1 < 0 的轨迹与 SKIPIF 1 < 0 轴围成的区域面积为两个 SKIPIF 1 < 0 圆的面积与 SKIPIF 1 < 0 的面积之和，
即所求面积为 SKIPIF 1 < 0 ，D正确.故选：ACD.
4．《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积＝ SKIPIF 1 < 0 (弦×矢＋矢 SKIPIF 1 < 0 )．弧田是由圆弧及其所对的弦所围成．公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为 SKIPIF 1 < 0 ，半径等于4米的弧田，按照上述经验公式计算所得弧田面积最接近的整数是 ．
【答案】9
【详解】设弧田的圆心为 SKIPIF 1 < 0 ，弦为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为 SKIPIF 1 < 0 中点，连 SKIPIF 1 < 0 交弧于 SKIPIF 1 < 0 ，如图所示，
由题意可得∠AOB＝ SKIPIF 1 < 0 ，OA＝4，在Rt△AOC中，易得∠AOC＝ SKIPIF 1 < 0 ，∠CAO＝ SKIPIF 1 < 0 ，
OC＝ SKIPIF 1 < 0 OA＝ SKIPIF 1 < 0 ，可得矢＝4－2＝2，由AC＝OA SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 ，可得弦AB＝2AC＝ SKIPIF 1 < 0 ，
所以弧田面积＝ SKIPIF 1 < 0 ×( SKIPIF 1 < 0 )＝ SKIPIF 1 < 0 ，因为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，从而 SKIPIF 1 < 0 ，
因此，所得弧田面积最接近的整数是9.故答案为：9.
5．已知扇形的面积为S，周长为p，中心角为 SKIPIF 1 < 0 .
(1)若S是定值，则当 SKIPIF 1 < 0 为多少弧度时，周长p最小，并求此最小值（用S表示）.
(2)若p是定值，则当 SKIPIF 1 < 0 为多少弧度时，面积S最大，并求此最大值（用p表示）.
【答案】(1)当 SKIPIF 1 < 0 时周长最小，为 SKIPIF 1 < 0 (2)当 SKIPIF 1 < 0 时面积最小，为 SKIPIF 1 < 0
【详解】（1）依题意，设扇形的半径为 SKIPIF 1 < 0 ，则扇形的面积 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时，周长取得最小值 SKIPIF 1 < 0 .
（2）扇形周长 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时，扇形面积取得最大值 SKIPIF 1 < 0 ．
6．某地政府部门欲做一个“践行核心价值观”的宣传牌，该宣传牌形状是如图所示的扇形环面(由扇形 SKIPIF 1 < 0 挖去扇形 SKIPIF 1 < 0 后构成的)．已知 SKIPIF 1 < 0 米， SKIPIF 1 < 0 米 SKIPIF 1 < 0 ，线段 SKIPIF 1 < 0 、线段 SKIPIF 1 < 0 与弧 SKIPIF 1 < 0 、弧 SKIPIF 1 < 0 的长度之和为 SKIPIF 1 < 0 米，圆心角为 SKIPIF 1 < 0 弧度．
(1)求 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的函数解析式；
(2)记该宣传牌的面积为 SKIPIF 1 < 0 ，试问 SKIPIF 1 < 0 取何值时， SKIPIF 1 < 0 的值最大?并求出最大值．
【答案】(1) SKIPIF 1 < 0 ；(2)当 SKIPIF 1 < 0 时，y的值最大，最大值为 SKIPIF 1 < 0 ．
【详解】（1）根据题意，弧 SKIPIF 1 < 0 的长度为 SKIPIF 1 < 0 米，弧 SKIPIF 1 < 0 的长度 SKIPIF 1 < 0 米，
SKIPIF 1 < 0 ， SKIPIF 1 < 0 SKIPIF 1 < 0 ．
（2）依据题意，可知 SKIPIF 1 < 0 ，化简得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．∴当 SKIPIF 1 < 0 时，y的值最大，且最大值为 SKIPIF 1 < 0 ．课程标准
学习目标
①理解并掌握正角、负角、零角的概念。
②掌握象限角的范围，掌握终边相同的角的表示方法及判定方法。
③了解弧度制，能进行弧度与角度的互
化。
④由圆周角找出弧度制与角度制的联系，记住常见特殊角对应的弧度数。
⑤掌握弧度制中扇形的弧长公式和面积公式，能用公式进行简单的弧长及面积运算。
1.通过本节课的学习，要求掌握任意角的概念，并能用集合的形式表示任意角；
2掌握弧度制与角度制的互化，；
3.记住特殊角的弧度制；
4.掌握与弧度制相关的弧长公式和面积公式的运用；
第一象限角
SKIPIF 1 < 0
第二象限角
SKIPIF 1 < 0
第三象限角
SKIPIF 1 < 0 或 SKIPIF 1 < 0
第四象限角
SKIPIF 1 < 0 或 SKIPIF 1 < 0
①
终边落在 SKIPIF 1 < 0 轴非负半轴
SKIPIF 1 < 0
②
终边落在 SKIPIF 1 < 0 轴非负半轴
SKIPIF 1 < 0
③
终边落在 SKIPIF 1 < 0 轴非正半轴
SKIPIF 1 < 0 或 SKIPIF 1 < 0
④
终边落在 SKIPIF 1 < 0 轴非正半轴
SKIPIF 1 < 0 或 SKIPIF 1 < 0
⑤
终边落在 SKIPIF 1 < 0 轴
SKIPIF 1 < 0
⑥
终边落在 SKIPIF 1 < 0 轴
SKIPIF 1 < 0 或 SKIPIF 1 < 0
⑦
终边落在坐标轴
SKIPIF 1 < 0
角度制
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
弧制度
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0