人教版八年级数学上册专项素养综合练(二)全等三角形的六种常见模型课件

这是一份人教版八年级数学上册专项素养综合练(二)全等三角形的六种常见模型课件，共27页。

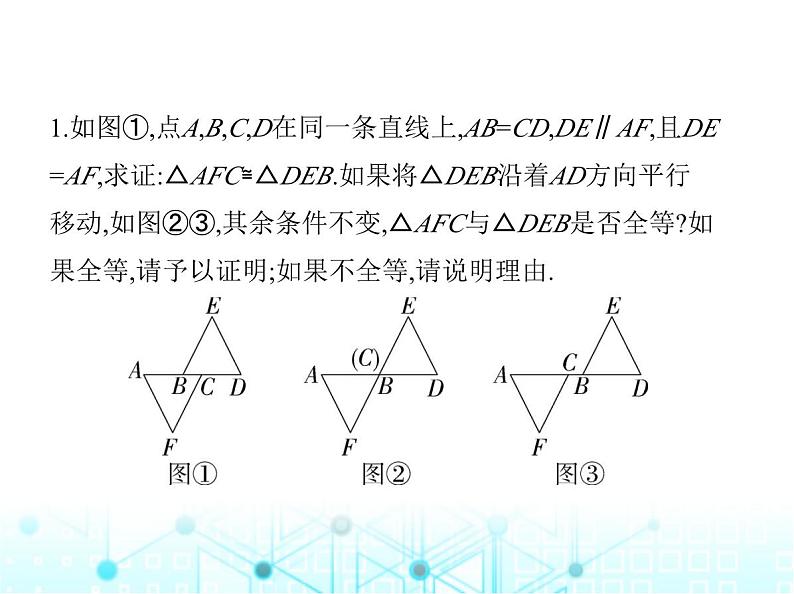
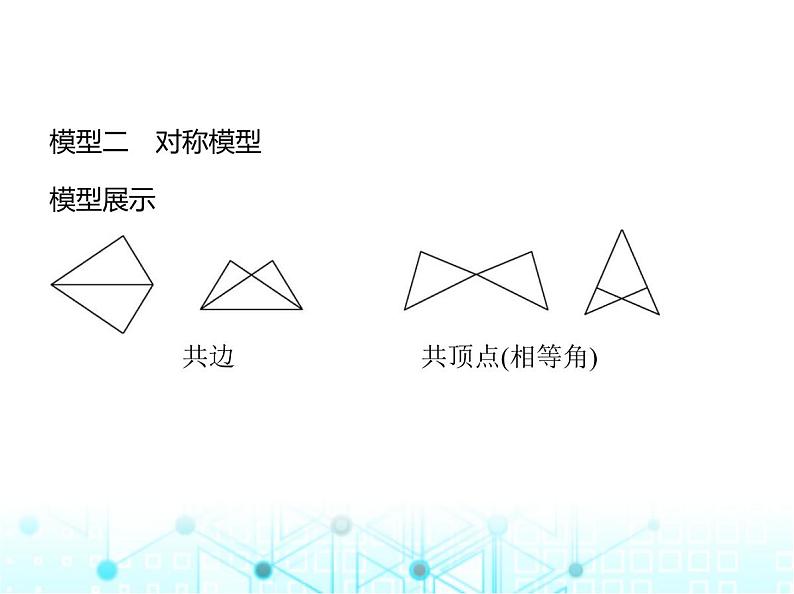
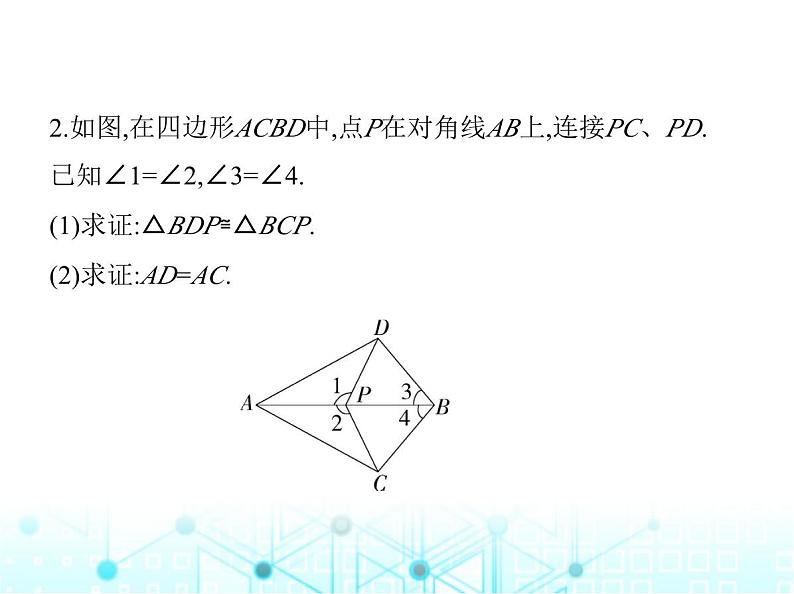
专项素养综合练(二)全等三角形的六种常见模型模型一　平移模型模型展示     ①通过平行找相等角;②通过加(减)公共线段找相等边.1.如图①,点A,B,C,D在同一条直线上,AB=CD,DE∥AF,且DE=AF,求证:△AFC≌△DEB.如果将△DEB沿着AD方向平行移动,如图②③,其余条件不变,△AFC与△DEB是否全等?如果全等,请予以证明;如果不全等,请说明理由.  证明　∵AB=CD,∴AB+BC=CD+BC,即AC=BD.∵DE∥AF,∴∠A=∠D.在△AFC和△DEB中, ∴△AFC≌△DEB(SAS).在题图②③中,△AFC与△DEB全等.证明:在题图②中,∵DE∥AF,∴∠A=∠D.在△AFC和△DEB中, ∴△AFC≌△DEB(SAS).在题图③中,∵AB=CD,∴AB-BC=CD-BC,即AC=BD,∵AF∥DE,∴∠A=∠D.在△AFC和△DEB中, ∴△AFC≌△DEB(SAS).模型二　对称模型模型展示     　　　　　共边　　　　　　　共顶点(相等角)2.如图,在四边形ACBD中,点P在对角线AB上,连接PC、PD.已知∠1=∠2,∠3=∠4.(1)求证:△BDP≌△BCP.(2)求证:AD=AC.  证明    (1)∵∠1=∠2,∠1+∠DPB=180°,∠2+∠CPB=180°,∴∠DPB=∠CPB,在△BDP和△BCP中, ∴△BDP≌△BCP(ASA).(2)由(1)知△BDP≌△BCP,∴DP=CP,在△ADP和△ACP中, ∴△ADP≌△ACP(SAS),∴AD=AC.模型三　旋转模型模型展示     　　　　　共顶点　　　　　　　　不共顶点3.已知:如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:∠ADE=∠AED.  证明　∵AB⊥AC,AD⊥AE,∴∠BAC=∠DAE=90°,∴∠BAD+∠DAC=∠DAC+∠CAE,∴∠BAD=∠CAE,在△ABD与△ACE中, ∴△ABD≌△ACE(ASA),∴AD=AE,∴Rt△AFD≌Rt△AFE,∴∠ADE=∠AED.过点A作AF⊥DE,垂足为F(图略),在Rt△AFD与Rt△AFE中, 模型四　手拉手模型模型展示               条件:AB=AC,AD=AE,∠BAC=∠DAE.结论:△ABD≌△ACE.4.如图,AE=AB,AC=AF,∠BAE=∠CAF=90°,EC、BF相交于点M.(1)求证:EC=BF.(2)求证:EC⊥BF.(3)若将条件∠BAE=∠CAF=90°改为∠BAE=∠CAF=m°,则(1)(2)中的结论还成立吗?(1)中的结论　　　　    ,(2)中的结论　　　　    (填“成立”或“不成立”).解析    (1)证明:∵∠BAE=∠CAF=90°,∴∠BAE+∠BAC=∠CAF+∠BAC,即∠CAE=∠BAF,在△EAC与△BAF中, ∴△EAC≌△BAF,∴EC=BF.(2)证明:如图,设AC交BF于O. 由(1)知△EAC≌△BAF,∴∠AFO=∠OCM,∵∠AOF=∠COM,∴∠OMC=∠OAF=90°,∴EC⊥BF.(3)(1)中的结论成立,(2)中的结论不成立.提示:同法可证△EAC≌△BAF,可得EC=BF,易得∠CMF=∠FAC=m°,∴(1)中的结论成立,(2)中的结论不成立.模型五　一线三等角模型模型展示               通过“三等角”信息得到一组相等的角,另找一条边相等,即可证全等.5.(1)如图1,已知△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.求证:DE=BD+CE.(2)如图2,在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC.请写出DE,BD,CE三条线段的数量关系,并说明理由. 图1 图2解析    (1)证明:∵BD⊥直线m,CE⊥直线m,∴∠BDA=∠CEA=90°,∴∠BAD+∠ABD=90°,∵∠BAC=90°,∴∠BAD+∠CAE=90°,∴∠CAE=∠ABD,在△ADB和△CEA中, ∴△ADB≌△CEA(AAS),∴AE=BD,AD=CE,∴DE=AE+AD=BD+CE.(2)DE=BD+CE.理由如下:∵∠BDA=∠BAC,∴∠DBA+∠BAD=∠BAD+∠CAE,∴∠DBA=∠CAE,在△ADB和△CEA中, ∴△ADB≌△CEA(AAS),∴BD=AE,AD=CE,∴DE=AE+AD=BD+CE.模型六　中点模型模型展示    点D为BC的中点.延长AD至E,使DE=AD,连接CE作BE⊥AD作BE⊥AD,CF⊥AD6.八年级一班数学兴趣小组在一次活动中进行了探究实验活动,请你和他们一起活动吧.【探究与发现】(1)如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中全等的两个三角形:　　　　    .【理解与应用】(2)如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是     .(3)在△ABC中,D为BC的中点,M为AC的中点,连接BM交AD于F,若∠AFM=∠MAF,求证:BF=AC.图1  图2    图3解析    (1)△ADC≌△EDB.提示:在△ADC和△EDB中, ∴△ADC≌△EDB(SAS).(2)如图,延长EP至点Q,使PQ=PE,连接FQ, 在△PED与△PQF中, ∴△PED≌△PQF(SAS),∴FQ=DE=3,在△EFQ中,EF-FQ