



青岛版(2024)八年级上册2.6 等腰三角形精品课件ppt
展开三边都相等的三角形叫等边三角形
等边三角形是一种特殊的等腰三角形
由于等边三角形是特殊的等腰三角形,因此它具有等腰三角形的所有性质,除此之外,它还有哪些特有的性质呢?怎样判定一个三角形是等边三角形呢?
2.6 等腰三角形
探索并掌握等边三角形的性质
探索并掌握等边三角形的判定方法
能运用等边三角形的性质与判定解决相关问题
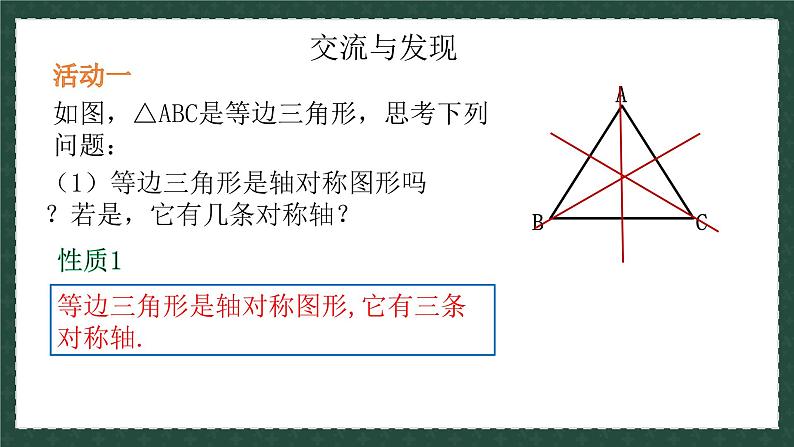
(1)等边三角形是轴对称图形吗?若是,它有几条对称轴?
等边三角形是轴对称图形,它有三条对称轴.
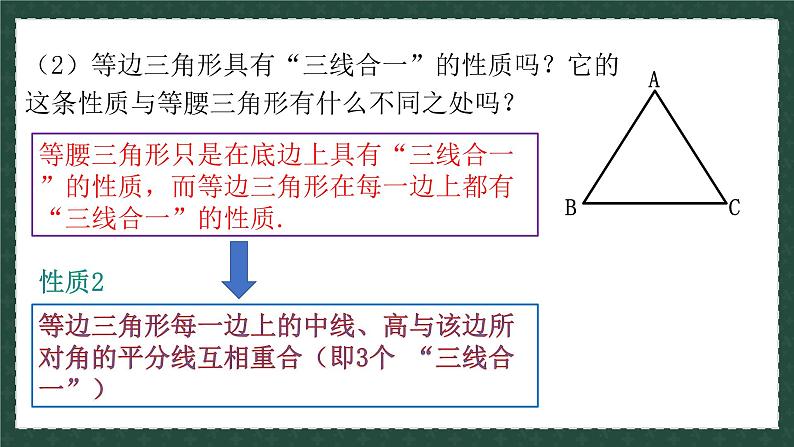
等腰三角形只是在底边上具有“三线合一”的性质,而等边三角形在每一边上都有“三线合一”的性质.
(2)等边三角形具有“三线合一”的性质吗?它的这条性质与等腰三角形有什么不同之处吗?
等边三角形每一边上的中线、高与该边所对角的平分线互相重合(即3个 “三线合一”)
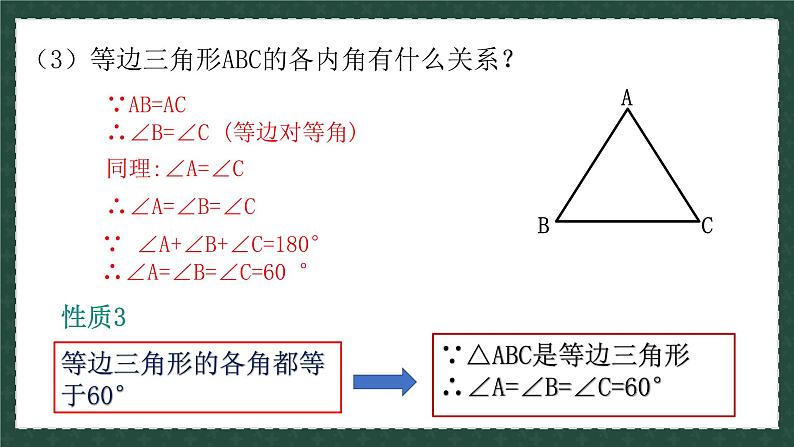
(3)等边三角形ABC的各内角有什么关系?
∵ ∠A+∠B+∠C=180° ∴∠A=∠B=∠C=60 °
∵AB=AC∴∠B=∠C (等边对等角)
等边三角形的各角都等于60°
∵△ABC是等边三角形∴∠A=∠B=∠C=60°
根据等边三角形定义可判断一个三角形是等边三角形,除此之外,还有其他的判定方法吗?
思考下列问题:(1)三个角都相等的三角形是等边三角形吗?(2)有一个角为60°的等腰三角形是等边三角形吗?
学习指导①大家以小组为单位进行合作探究②探究过程中,有疑难问题可向老师询问③时间约为5分钟,5分钟后由小组代表进行展示
∵ ∠B=∠C∴ AB=AC
∴ △ABC是等边三角形
三个角都相等的三角形是等边三角形吗?
三个角都相等的三角形是等边三角形
∵∠A=∠B=∠C∴△ABC是等边三角形
有一个角为60°的等腰三角形是等边三角形吗?
如图在△ABC中,AB=AC.
(1)当∠B=60°时∵AB=AC.∴∠B=∠C=60°∴∠A=180°-∠B-∠C=60°∴∠A=∠B=∠C ∴△ABC是等边三角形
(2)当 A= 60°时∠B+∠C=180°-∠A=120°∵AB=AC.∴∠B=∠C∴∠B=∠C=60 °∴∠A=∠B=∠C 所以△ABC是等边三角形.
有一个角是60°的等腰三角形是等边三角形
∵AB=AC,∠C=60°∴△ABC是等边三角形
学习小心得已知三边关系,选用定义判断;已知三角关系,选用判定方法1;已知三角形是等腰三角形,选用判定方法2.
例1已知:△ABC和△CDE是直线BD同侧的两个等边三角形,连接BE、AD.分别交AC、CE于点F、G.并连接FG。 求证:(1)BE=AD;
例1已知:△ABC和△CDE是直线BD同侧的两个等边三角形,连接BE、AD.分别交AC、CE于点F、G.并连接FG。求证:(2)△CFG是等边三角形。
1.下列说法:①在△ABC中,AB=AC且∠A=∠B,则△ABC是等边三角形②在△ABC中,∠A=∠B=60°,则△ABC是等边三角形③在△ABC中,AB=AC且∠B=60°,则△ABC是等边三角形三个外角④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的有( )A.①②③ B.①②④ C.①③ D.①②③④
3.已知:△ABC是等边三角形,AD⊥BC,点E是AC上的一点,且AE=AD.求:∠EDC的度数。
4.如图所示,AD是的∠BAC角平分线,EF是AD的垂直平分线,分别交AB、AC于点E、F,连结DE,若DE=EF,试判断△AEF的形状,并说明理由.
1.如图,△ABC是等边三角形,且∠BAD=∠CBE=∠ACF. 求证:△DEF是等边三角形。
2.已知:在Rt△ABC中,∠C=90°,∠A=30°.试说明BC与斜边AB的数量关系
数学八年级上册第2章 图形的轴对称2.6 等腰三角形优质课课件ppt: 这是一份数学八年级上册<a href="/sx/tb_c92985_t3/?tag_id=26" target="_blank">第2章 图形的轴对称2.6 等腰三角形优质课课件ppt</a>,共18页。PPT课件主要包含了第二章图形的轴对称,青岛版八年级数学上册,第一课时,学习目标,实验与探究,AD垂直平分BC,AD垂直BC,AD平分BC,∠BAD∠CAD,∠B∠C等内容,欢迎下载使用。
初中数学青岛版八年级上册第2章 图形的轴对称2.6 等腰三角形优秀课件ppt: 这是一份初中数学青岛版八年级上册<a href="/sx/tb_c92985_t3/?tag_id=26" target="_blank">第2章 图形的轴对称2.6 等腰三角形优秀课件ppt</a>,文件包含261等腰三角形原卷版docx、261等腰三角形解析版docx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
初中数学青岛版八年级上册1.3 尺规作图精品ppt课件: 这是一份初中数学青岛版八年级上册<a href="/sx/tb_c92978_t3/?tag_id=26" target="_blank">1.3 尺规作图精品ppt课件</a>,共16页。PPT课件主要包含了第一章全等三角形,青岛版八年级数学上册,第二课时,学习目标,实验与探究,图1-28,确定三个顶点的位置,成果展示,图1-29,①作∠B∠α等内容,欢迎下载使用。













