




青岛版八年级上册1.3 尺规作图完美版课件ppt
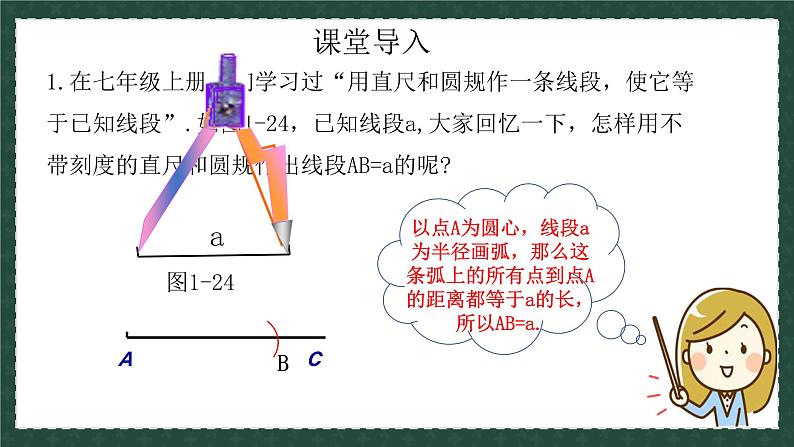
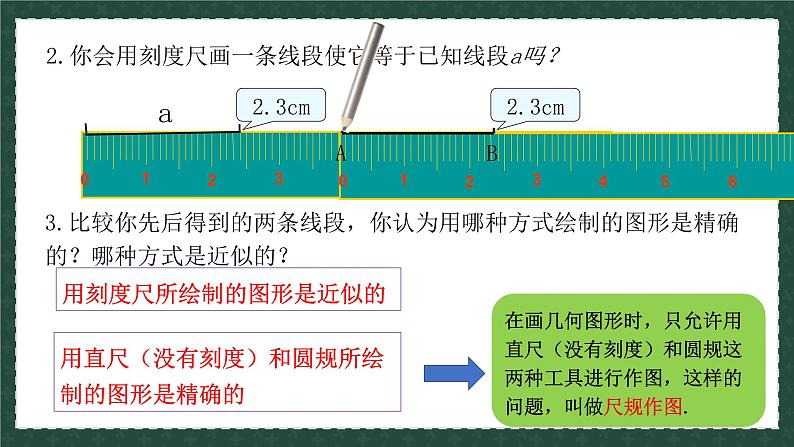
展开2.你会用刻度尺画一条线段使它等于已知线段a吗?
3.比较你先后得到的两条线段,你认为用哪种方式绘制的图形是精确的?哪种方式是近似的?
用直尺(没有刻度)和圆规所绘制的图形是精确的
用刻度尺所绘制的图形是近似的
在画几何图形时,只允许用直尺(没有刻度)和圆规这两种工具进行作图,这样的问题,叫做尺规作图.
1.3 尺 规 作 图
知道什么是尺规作图,了解尺规作图与使用其他工具画图的区别.
会利用尺规完成基本作图:作一个角等于已知角,并要掌握其步骤与原理.
通过尺规作图,让学生体会文字语言、符号语言以及图形语言之间的相互转化.
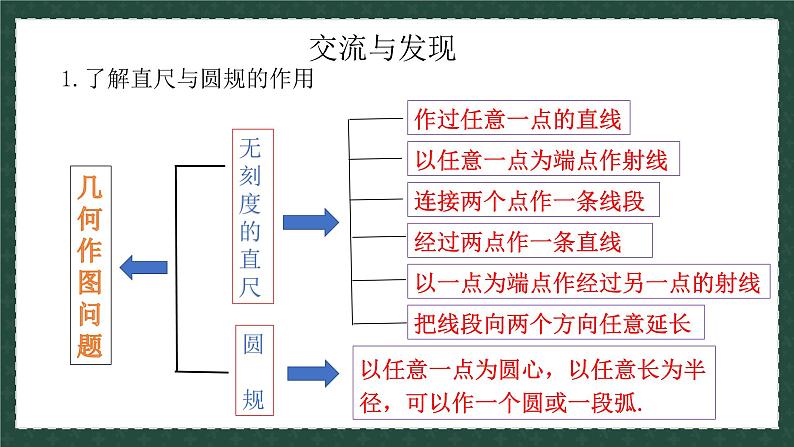
1.了解直尺与圆规的作用
以任意一点为端点作射线
以一点为端点作经过另一点的射线
把线段向两个方向任意延长
以任意一点为圆心,以任意长为半径,可以作一个圆或一段弧.
2.再看一个尺规作图问题
探究问题:已知∠AOB,你能用直尺和圆规作一个角∠A′O′B′,使∠A′O′B′=∠AOB吗?
我们知道,全等三角形对应角相等,因此可以首先利用直尺和圆规将∠AOB放到一个三角形(如△COD)中,使它成为△COD的一个内角;然后利用直尺和圆规作出一个与△COD全等的三角形,该三角形中∠AOB的对应角,就是所求作的角.
已知:∠AOB,求作:∠A′O′B′,使∠A′O′B′=∠AOB.
(2)用符号语言表示该题
①任取一点O′,作射线O′A′
②以点O为圆心,以任意长为半径作弧,交OA于点C,交OB于点D
③以点O′为圆心,以OC为半径作弧,交射线O′A′于点C′
④以点C′为圆心,以CD为半径作弧,与前弧交于点D′
⑤过点D′作射线O′B′
∠A′O′B′就是所求作的角.
思考:你能说出∠A′O′B′=∠AOB的理由吗?
在上图中,分别连接CD与C′D′,
由作图可知:OD=O'D',OC=O'C'CD=C'D'
由SSS可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB.
最基本、最常见的尺规作图,称为基本作图
作一条线段等于已知线段
例1:已知∠α,∠β, 求作:∠γ=∠α-∠β
(2)在∠AOB内,以点O为顶点, OB为一边,作∠BOC=∠β.
则∠AOC就是所要求作的∠γ
(1)作∠AOB=∠α
2.本书中的尺规作图,若没有特殊要求,通常不写作法,但要保留作图痕迹.
3.完成作图后,一定要指明哪一个图形是所要求作的图形.
1.作法中所需要的基本作图,通常不写步骤,只指明基本作图的类型即可.
解:①如图,先作∠COD=∠α
②再作∠DOG=∠β
那么∠COG就是所要求作的∠γ
2.如图,已知∠α,求作∠γ,使∠γ=2∠α(不写出作法,保留作图痕迹)
那么∠AOB就是所要求作的∠γ
3.已知直线AB和直线AB上一点P,你能利用尺规作直线CD,使CD∥AB吗?
那么直线CD就是所要求作的图形
1.如下所示的尺规作图题,题中符号代表的内容正确的是( ) 如图,已知∠AOB,求作:∠DEF,使 ∠DEF=∠AOB作法: (1)以①为圆心,任意长为半径画弧,分别交OA、OB于点P、Q; (2)作射线EG,并以点E为圆心,②长为半径画弧交EG于点D; (3)以点D为圆心③长为半径画弧交(2)步中所画弧于点F; (4)作④,∠DEF即为所求作的角.
A. ①表示点EB. ②表示PQC. ③表示OQD. ④表示射线EF
数学2.5 解直角三角形的应用精品课件ppt: 这是一份数学<a href="/sx/tb_c99061_t3/?tag_id=26" target="_blank">2.5 解直角三角形的应用精品课件ppt</a>,共21页。PPT课件主要包含了2边之间的关系,1角之间的关系,两条边或一边一角,温故知新,转化思想,情境导入,能力拔高,课堂小结等内容,欢迎下载使用。
青岛版九年级上册2.5 解直角三角形的应用优秀ppt课件: 这是一份青岛版九年级上册<a href="/sx/tb_c99061_t3/?tag_id=26" target="_blank">2.5 解直角三角形的应用优秀ppt课件</a>,共17页。PPT课件主要包含了有关实际问题,解直角三角形问题,求出有关的边或角,问题答案,课堂导入,探究新知,课堂练习等内容,欢迎下载使用。
青岛版九年级上册2.5 解直角三角形的应用试讲课ppt课件: 这是一份青岛版九年级上册<a href="/sx/tb_c99061_t3/?tag_id=26" target="_blank">2.5 解直角三角形的应用试讲课ppt课件</a>,共20页。PPT课件主要包含了课堂导入,探究新知,有关实际问题,解直角三角形问题,求出有关的边或角,问题答案,课堂练习等内容,欢迎下载使用。













