






苏科版八年级上册6.4 用一次函数解决问题教课课件ppt
展开1.(跨学科·物理)(2023山西中考)一种弹簧秤最大能称不超过 10 kg的物体,不挂物体时弹簧的长为12 cm,每挂重1 kg物体, 弹簧伸长0.5 cm,在弹性限度内,挂重物后弹簧的长度y(cm)与 所挂物体的质量x(kg)之间的函数关系式为 ( )
知识点1 建立一次函数模型解决实际问题
A.y=12-0.5x B.y=12+0.5x C.y=10+0.5x D.y=0.5x
解析 根据不挂物体时弹簧的长为12 cm,每挂重1 kg物体, 弹簧伸长0.5 cm,可得在弹性限度内,挂x kg的物体,弹簧伸长 了0.5x cm,则挂重物后弹簧的长度为(12+0.5x)cm,所以y=12+ 0.5x(0≤x≤10).故选B.
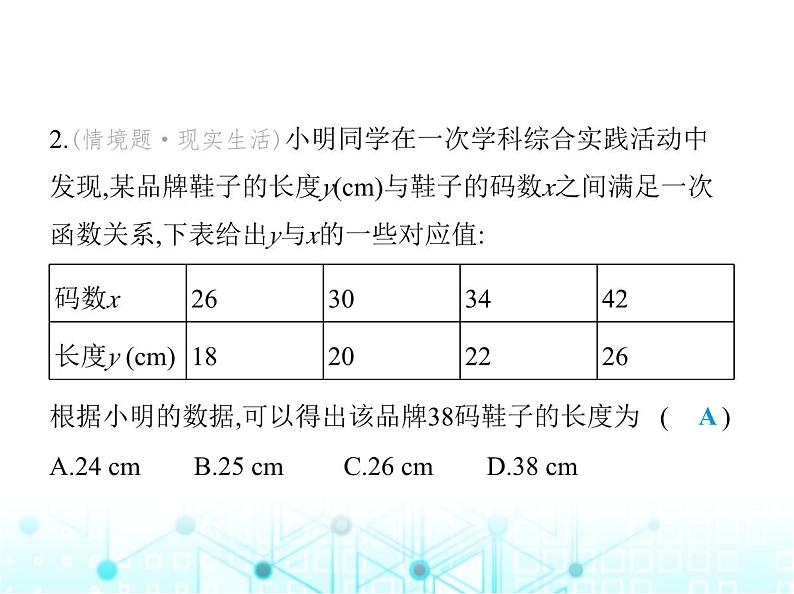
2.(情境题·现实生活)小明同学在一次学科综合实践活动中 发现,某品牌鞋子的长度y(cm)与鞋子的码数x之间满足一次 函数关系,下表给出y与x的一些对应值:
根据小明的数据,可以得出该品牌38码鞋子的长度为 ( )A.24 cm B.25 cm C.26 cm D.38 cm
解析 设y与x的函数解析式为y=kx+b.∵点(26,18),(30,20)在该函数图像上,∴ 解得 即y与x的函数解析式为y=0.5x+5,当x=38时,y=0.5×38+5=24.故选A.
3.(新独家原创)已知A地到B地的路程约为900千米,一辆汽车从A地出发开往B地,若其平均速度为100千米/小时,则这辆汽车距离B地的路程s(千米)与所行驶的时间t(小时)之间的函数关系式是 (写出自变量t的取值范围).
s=900-100t(0≤t≤9)
解析 汽车走的路程为100t千米,则s=900-100t(0≤t≤9).
4.数学活动课上,同学们在探究“叠在一起的纸杯的总高度 随着纸杯数量的变化规律”时,发现每增加一个纸杯,叠在一 起的纸杯增加的高度是一样的.如图所示的是1个纸杯和若 干个规格相同的纸杯叠放在一起的示意图,纸杯的个数与纸 杯的高度的关系如表.
根据上表,回答以下问题.(1)表中有两个变量,分别是 和 .(2)请同学们用自己喜欢的字母表示上述两个变量,建立一个 函数关系,用来描述纸杯的总高度随着纸杯数量的变化规律.(3)若有25个上述规格的纸杯,求其叠放在一起的高度.
解析 (1)纸杯的个数;纸杯的高度.(2)设纸杯为x个时,高度是y cm,从题表可知y与x满足一次函 数关系,设y=kx+b,将(1,9),(2,9.5)代入,得 解得 ∴y=0.5x+8.5.(3)当x=25时,y=0.5×25+8.5=21.答:若有25个题目所述规格的纸杯,其叠放在一起的高度是21 cm.
5.(教材变式·P159T1)拖拉机开始工作时,油箱中有油30 L,每 小时耗油5 L.(1)写出油箱中的余油量Q(L)与工作时间t(h)之间的函数关系 式.(2)写出自变量t的取值范围.(3)拖拉机工作2小时后,油箱余油量是多少?(4)若油箱中余油量为10 L,则拖拉机工作了几小时?
解析 (1)由题意可得,油箱中的余油量Q(L)与工作时间t(h) 之间的函数关系式是Q=30-5t.(2)当Q=0时,0=30-5t,解得t=6,∴自变量t的取值范围是0≤t≤6.(3)当t=2时,Q=30-5×2=20,∴拖拉机工作2小时后,油箱余油量是20 L.(4)当Q=10时,10=30-5t,解得t=4.∴拖拉机工作了4个小时.
6.如图,l1反映了某公司某种产品的销售收入与销售量的关 系,l2反映了该种产品的销售成本与销售量的关系.根据图像 提供的信息,下列说法正确的是 ( )
知识点2 利用图像解决实际问题
A.当销售量为2吨时,销售成本是2 000元B.当销售成本是5 000元时,该公司的该产品盈利C.l2的函数表达式为y=400x+2 000D.当销售量为5吨时,该公司的该产品盈利1 000元
解析 A.当销售量为2吨时,销售成本是3 000元,故选项A说 法错误,不符合题意;B.当销售成本是5 000元时,销售收入是6 000元,该公司的该产品盈利,故选项B说法正确,符合题意;C. 设l2的解析式为y=kx+b,把(0,2 000),(4,4 000)代入解析式,得 解得 故l2的解析式为y=500x+2 000,选项C说法错误,不符合题意;D.当销售量为5吨时,y=500×5+2 000=4 500,该公司的该产品盈利5 000-4 500=500元,故选项 D说法错误,不符合题意.故选B.
7.(跨学科·生物)(2023北京东城期中)某生物小组观察一植物 生长,得到植物高度y(单位:厘米)与观察时间x(单位:天)之间 的关系,并画出如图所示的图像(AC是线段,射线CD平行于x 轴).在第 天后植物的高度不变,该植物最高为 厘米.
解析 ∵CD∥x轴,∴从第50天开始植物的高度不变.设线段AC的解析式为y=kx+b(k≠0)(0≤x≤50).∵线段AC经过点A(0,6),B(30,12),∴ 解得 ∴线段AC的解析式为y= x+6(0≤x≤50),当x=50时,y= ×50+6=16.
∴该植物最高为16厘米.故答案为50;16.
8.(2022江苏盐城中考)小丽从甲地匀速步行去乙地,小华骑 自行车从乙地匀速前往甲地,同时出发.两人离甲地的距离y (m)与出发时间x(min)之间的函数关系如图所示.(1)小丽步行的速度为 m/min.(2)当两人相遇时,求他们到甲地的距离.
解析 (1)由题图像可知,小丽步行的速度为 =80(m/min).故答案为80.(2)由题图像可得,小华骑自行车的速度是 =120(m/min),∴出发 =12 min后两人相遇,∴相遇时小丽所走的路程为12×80=960 m,即当两人相遇时,他们到甲地的距离是960 m.
9.(新考法)(2023湖北武汉中考,10,★★★)皮克定理是格点几 何学中的一个重要定理,它揭示了以格点为顶点的多边形的 面积S=N+ L-1,其中N,L分别表示这个多边形内部与边界上的格点个数,在平面直角坐标系中,横、纵坐标都是整数的点 为格点.已知A(0,30),B(20,10),O(0,0),则△ABO内部的格点个 数是 ( )A.266 B.270 C.271 D.285
解析 本题把皮克定理与一次函数相结合,考法比较新颖.由 A(0,30)可知边OA上有31个格点(含点O,A).∵由题意易得直线OB的解析式为y= x,∴当x为小于或等于20的正偶数时,y也为整数,即OB边上有10个格点(不含端点O, 含端点B).∵由题意易得直线AB的解析式为y=-x+30,∴当0
(3)两车相遇后,如果快车以返回的速度继续向甲地行驶,求 到达甲地还需多长时间.
解析 (1)点A的实际意义是出发3小时,快车到达乙地,此时 快车与慢车相距120 km.(2)∵点B的横坐标为3+ =3.5,点B的纵坐标为120- ×70=85,∴点B的坐标为(3.5,85).设线段AB所表示的函数表达式为y=kx+b,将A(3,120),B(3.5,8 5)代入,得 解得 ∴线段AB所表示的函数表达式为y=-70x+330(3≤x≤3.5).(3)∵快车从返回到遇见慢车所用的时间为4-3.5=0.5(h),
∴快车从乙地返回甲地时的速度为85÷0.5-70=100(km/h).∵4×70÷100=2.8(h),∴两车相遇后,如果快车以返回的速度继续向甲地行驶,到达 甲地还需2.8 h.
11.(2023江苏扬州中考,26,★★☆)近年来,市民交通安全意 识逐步增强,头盔需求量增大.某商店购进甲、乙两种头盔, 已知购买甲种头盔20只,乙种头盔30只,共花费2 920元,甲种 头盔的单价比乙种头盔的单价高11元.(1)甲、乙两种头盔的单价各是多少元?(2)商店决定再次购进甲、乙两种头盔共40只,正好赶上厂家 进行促销活动,促销方式如下:甲种头盔按单价的八折出售,
乙种头盔每只降价6元出售.如果此次购买甲种头盔的数量 不低于乙种头盔数量的一半,那么应购买多少只甲种头盔,使此次购买头盔的总费用最小?最小费用是多少元?
解析 (1)设甲种头盔的单价为x元,乙种头盔的单价为y元.根 据题意,得 解得 答:甲种头盔单价是65元,乙种头盔单价是54元.(2)设再次购进甲种头盔m只,总费用为w元,则再次购进乙种 头盔(40-m)只.根据题意,得m≥ (40-m),解得m≥ ,w=65×0.8m+(54-6)(40-m)=4m+1 920.
∵4>0,∴w随着m增大而增大,∴当m=14时,w取得最小值,即购买14只甲种头盔时,总费用最小,最小费用为14×4+1 920 =1 976(元).答:购买14只甲种头盔时,总费用最小,最小费用为1 976元.
12.(应用意识)(2023黑龙江龙东地区中考)已知甲、乙两地相 距480 km,一辆出租车从甲地出发往返于甲、乙两地,一辆货 车沿同一条公路从乙地前往甲地,两车同时出发.货车途经服 务区,停下来装完货物后,发现此时与出租车相距120 km,货 车继续出发 h后与出租车相遇.出租车到达乙地后立即按原路返回,结果比货车早15分钟到达甲地.如图所示的是两车 距各自出发地的距离y(km)与货车行驶时间x(h)之间的函数 图像,结合图像回答下列问题.
(1)图中a的值是 .(2)求货车装完货物后驶往甲地的过程中,距其出发地的距离 y(km)与行驶时间x(h)之间的函数关系式.(3)直接写出在出租车返回的行驶过程中,货车出发多长时间 与出租车相距12 km.
解析 (1)由题图像知,点C的坐标是(4,480).设直线OC的解析式为y=kx,把C(4,480)代入,得480=4k,解得k= 120,∴直线OC的解析式为y=120x.把(1,a)代入y=120x,得a=12 0.故答案为120.(2)∵a=120,∴货车卸货时与乙地相距120 km,∴出租车距离乙地120+120=240 km,∴出租车距离甲地480-240=240 km.把y=240代入y=120x,得240=120x,解得x=2,
∴货车装完货物时,x=2,∴B(2,120),根据货车继续出发 h后与出租车相遇,可得 ×(出租车的速度+货车的速度)=120,根据直线OC的解析式为y=120x(0≤x≤4),可得出租车的速度为120 km/h,∴相遇时,货车的速度为120÷ -120=60 km/h,故可设直线BG的解析式为y=60x+b,将B(2,120)代入y=60x+b,可得120=120+b,
解得b=0,∴直线BG的解析式为y=60x(2≤x≤8),故货车装完货物后驶往甲地的过程中,距其出发地的距离y (km)与行驶时间x(h)之间的函数关系式为y=60x.(3)把y=480代入y=60x,可得480=60x,解得x=8,∴G(8,480),∴F(8,0).根据出租车到达乙地后立即按原路返回,结果比货车早15分 钟到达甲地,可得EF= = ,
∴E ,∴出租车返回时的速度为480÷ =128 km/h.设在出租车返回的行驶过程中,货车出发t小时,与出租车相 距12 km,此时货车距离乙地60t km,出租车距离乙地128(t-4)=(128t-51 2)km.①出租车和货车第二次相遇前,相距12 km时,可得60t-(128t-5
苏科版八年级上册6.4 用一次函数解决问题教学演示课件ppt: 这是一份苏科版八年级上册6.4 用一次函数解决问题教学演示课件ppt,共17页。PPT课件主要包含了k1b2,y2-2x+2,y1x+2,x-2,知识回顾,自学互助,由y1y2得,解得x100,当x100时,y1y2650等内容,欢迎下载使用。
初中数学苏科版八年级上册6.4 用一次函数解决问题背景图ppt课件: 这是一份初中数学苏科版八年级上册6.4 用一次函数解决问题背景图ppt课件,共20页。PPT课件主要包含了情境导入,如何解决这个问题,方法一算术解法,方法二方程解法,解得x=1096,数年后雪线海拔,4500m,数年内雪线上升总高度,探寻数量关系,实际问题等内容,欢迎下载使用。
初中数学苏科版八年级上册第六章 一次函数6.4 用一次函数解决问题集体备课课件ppt: 这是一份初中数学苏科版八年级上册第六章 一次函数6.4 用一次函数解决问题集体备课课件ppt,共11页。PPT课件主要包含了如何解决这个问题,问题2,S105t+35,y2=1200x,解得x>40,变式训练,中考链接等内容,欢迎下载使用。













