




数学八年级上册6.4 用一次函数解决问题图文ppt课件
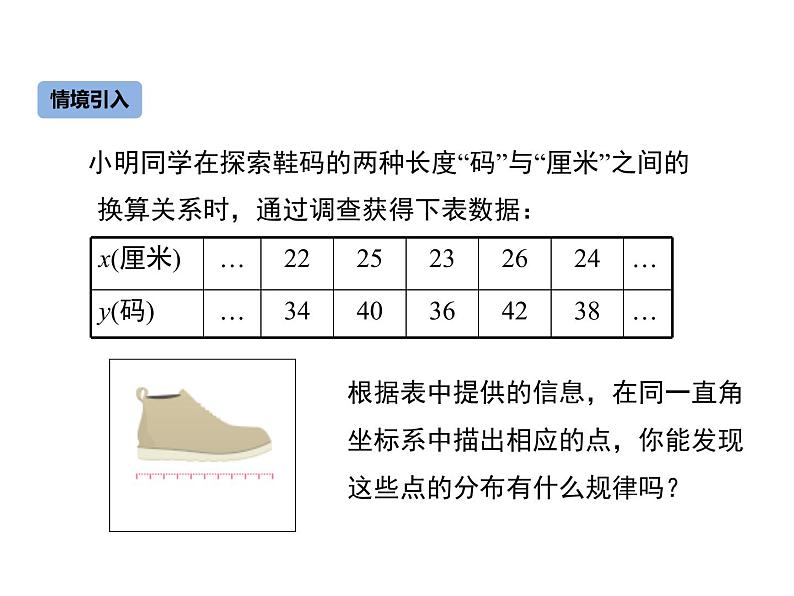
展开小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
根据表中提供的信息,在同一直角坐标系中描出相应的点,你能发现这些点的分布有什么规律吗?
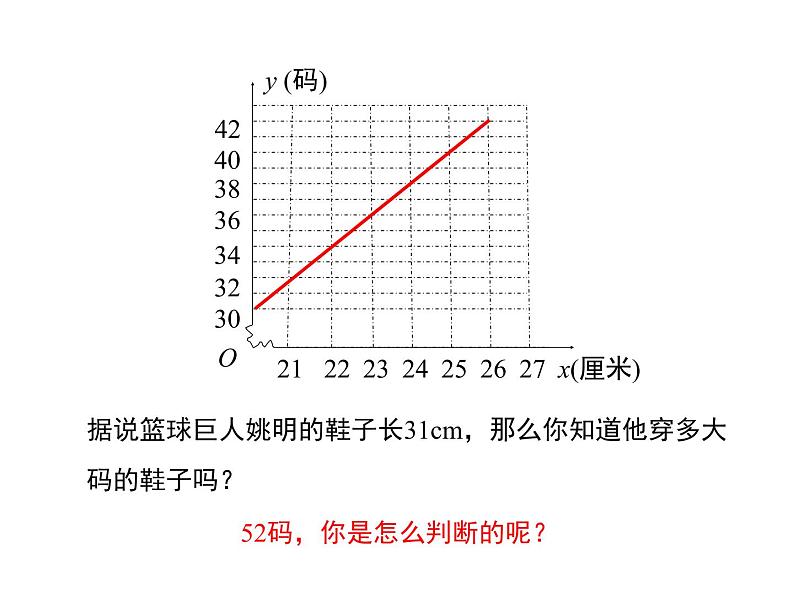
据说篮球巨人姚明的鞋子长31cm,那么你知道他穿多大码的鞋子吗?
52码,你是怎么判断的呢?
例1.某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售1件产品,奖励工资10元.
1.设某销售员销售产品x件,他应得的工资记为y元.求y与x之间的函数关系式.
2.用求出的函数关系式,解决下列问题(1)某销售员的工资为4100元,他这个月销售了多少件产品?
当y=4100时,4100=10x+3000.解得x=110.
(2)要使月工资超过4500元,该月的销售量应当超过多少件?
由题意得10x+3000>4500.解得x>150.
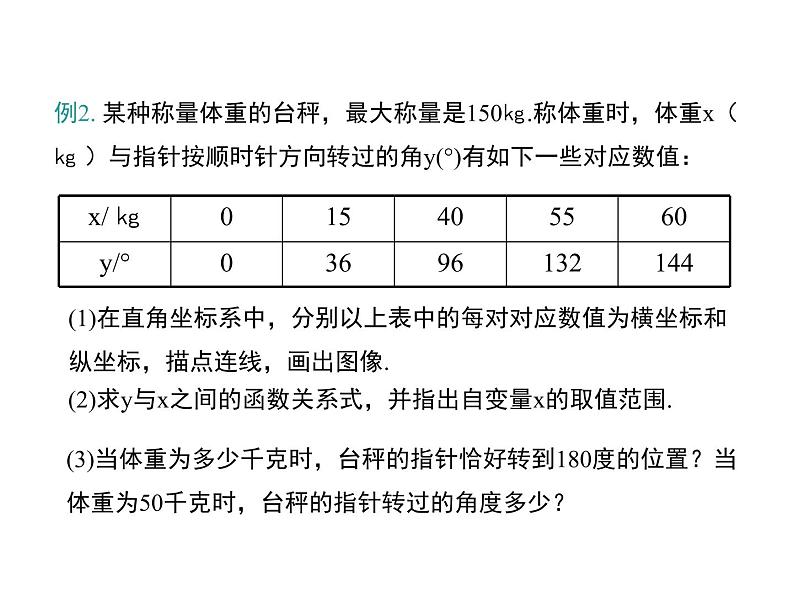
例2. 某种称量体重的台秤,最大称量是150㎏.称体重时,体重x( ㎏ )与指针按顺时针方向转过的角y(°)有如下一些对应数值:
(1)在直角坐标系中,分别以上表中的每对对应数值为横坐标和纵坐标,描点连线,画出图像.
(2)求y与x之间的函数关系式,并指出自变量x的取值范围.
(3)当体重为多少千克时,台秤的指针恰好转到180度的位置?当体重为50千克时,台秤的指针转过的角度多少?
(1)在直角坐标系中,分别以上表中的每对对应数值为横坐标和纵坐标,描点连线,画出图像.
(2)求y与x之间的函数关系式,并指出自变量x的取值范围.
分析:由表格给出的数据可以看出,每增加5千克,台秤的指针按顺时针方向旋转12度,所以y是x的正比例函数.
根据条件可得y=12/5x(0≤x≤150)
(3)当体重为多少千克时,台秤的指针恰好转到180度的位置?当体重为50千克时,台秤的指针转过的角度多少?
当y=180时,180=12/5x.解得x=75当x=50时,y=12/5×50=120.即当体重为75千克时,台秤的指针恰好转到180度的位置.当体重为50千克时,台秤的指针转过的角度是120度.
A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台,已知从A市调运一台机器到C村和D村的运费分别是400元和800元;从B市调运一台机器到C村和D村的运费分别是300元和500元.
① 设B市运往C市机器x台,求总运费W(元)关于x的函数关系式.
② 求总运费最低的调运方案的最低运费是多少.
分析① :A 市和 B 市库存机器共:( )台,C 村和D 村共需( )台,
B 市运到 C 村 台, B 市剩余 台运到 D 村
A 市运到 C 村 台, A 市剩余 台运到 D 村.
〔 12-(10-x)〕
分析② :先求出总运费的关系式,再对照一次函数最值相关问题具体分析.
解:① B 市运往 C 市机器x台,则有题意可知:W = 300x + 500 (6-x) + 400(10-x) +800〔12-(10-x)〕 = 200 x + 8600 ( 0 ≤ x ≤ 6 ) ∴总运费W(元)关于x的函数关系式为: W = 200 x + 8600 ( 0 ≤ x ≤ 6 )
② ∵ W = 200 x + 8600 ( 0 ≤ x ≤ 6 )是一次函数,且W随x的增大而增大 ∴当 x取最小值时,W 有最大值 即当 x = 0 时,W = 8600元 ∴ 总运费最低的调运方案的最低运费是8600元
一次函数“最大值”和“最小值”的产生和自变量的取值范围相辅相成: k > 0 ,a ≤ x ≤ c 时: x = a 时,y = ka + b 就是最小值,x = c 时,y = kc + b 就是最大值; k < 0 ,a ≤ x ≤ c 时: x = a 时, y = ka + b 就是最大值,x = c 时, y = kc+ b 就是最小值.
例4.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.(1)求出y关于x的函数关系式;(2)该市一户某月若用水x=10立方米时,求应缴水费;(3)该市一户某月缴水费26.6元,求该户这月用水量.
分析:(1)x≤8时,每立方米收费(1+0.3)元;(2)x>8时,超过的部分每立方米收费(1.5+1.2)元.
解:(1)y关于x的函数关系式为:
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)因为1.3×8=10.4<26.6,所以该用户用水量超过8立方米.
所以2.7x-11.2=26.6,解得x=14
答:应缴水费为15.8元
答:该户这月用水量为14吨
在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数,分段函数在生活中也有很多应用.
某市出租车的收费标准:不超过3km计费为7元,3km后按2.4元/km计费.
(1)写出车费y(元)与路程x(km)之间的函数关系式;
(1)当0
(2)小亮乘出租车出行,付费12.3元,你能算出小亮乘车的路程吗?(精确到0.1km)
∴12.3=7+2.4(x-3)
利用两个一次函数解决实际问题
由于小红比小明晚出发2 h,因此小红所用时间为(x - 2)h. 从而 y2 = 40(x - 2),自变量x 的取值范围是2≤x≤3.
(1)分别写出y1 ,y2与x之间的函数表达式;
过点(0,40)作射线l 与x 轴平行,它先与射线 y2 = 40(x - 2)相交,这表明小红先到达乙地.
(2)在同一个直角坐标系中,画出这两个函数的图象, 并指出谁先到达乙地.
甲骑自行车以10千米每小时的速度沿公路行驶,出发3小时后,乙骑摩托车从同一地点出发沿公路与甲同向行驶,速度为25千米每小时.设甲离开出发地的时间为x小时.
(2)写出乙离开出发地的路程y与x之间的函数关系式,并指出自变量x的取值范围;
y=25x-75(x≥3)
(1)写出甲离开出发地的路程y与x之间的函数关系式,并指出自变量x的取值范围;
由图可知,交点坐标是(5,50),即甲出发5小时后被乙追上,此时,两人距离出发地50千米
(3)在同一直角坐标系中,画出(1)(2)中函数的图像,并结合实际问题,解释图像中交点的意义.
例2 某单位有职工几十人,想在节假日期间组织到外地旅游.当地有甲、乙两家旅行社,它们服务质量基本相同,到此地旅游的价格都是每人100元.经联系协商,甲旅行社表示可给予每位游客八折优惠;乙旅行社表示单位先交1000元后,给予每位游客六折优惠.问该单位选择哪个旅行社,可使其支付的旅游总费用较少?
分析:假设该单位参加旅游人数为x,按甲旅行社的优惠条件,应付费用80x 元;按乙旅行社的优惠条件,应付费用(60x+1000)元.问题变为比较80x 与60x+1000 的大小了.
解法一:设该单位参加旅游人数为x.那么选甲旅行社,应付费用80x 元;选乙旅行社,应付(60x+1000)元 记 y1= 80x,y2= 60x+1000.在同一直角坐标系内作出两个函数的图象, y1与y2的图象交于点(50,4000).
解:观察图象,可知:当人数为50时,选择甲或乙旅行社费用都一样;当人数为0~49人时,选择甲旅行社费用较少;当人数为51~100人时,选择乙旅行社费用较少.
解法二:(1)当y1=y2,即80x= 60x+1000时,x=50. 所以当人数为50时,选择甲或乙旅行社费用都一样;(2)当y1 > y2,即80x > 60x+1000时, 得x > 50. 所以当人数为51~100人时 ,选择乙旅行社费用较少;(3)当y1 < y2,即80x < 60x+1000时,得x<50. 所以当人数为0~49人时,选择甲旅行社费用较少;
解法三:设选择甲、乙旅行社费用之差为y, 则y=y1-y2=80x-(60x+1000)=20x-1000. 画出一次函数y= 20x-1000的图象如下图.
它与x轴交点为(50,0) 由图可知:(1)当x=50时,y=0,即y1=y2;(2)当x>50时,y > 0,即y1 > y2;(3)当x<50时,y <0,即y1 < y2.
某移动公司对于移动话费推出两种收费方式: A方案:每月收取基本月租费15元,另收通话费 为0.2元/min; B方案: 零月租费,通话费为0.3元/min. (1)试写出A,B两种方案所付话费y(元)与通话 时间t(min)之间的函数关系式;(2)在同一坐标系画出这两个函数的图象,并指出那 种付费方式合算?
(2)这两个函数的图象如下:
y = 15+0.2t
观察图象,可知:当通话时间为150min时,选择A或B方案费用一样;当通话时间少于150min时,选择A方案费合算;当通话时间多于150min时,选择B方案合算.
1.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:
(1) 求身高y与指距x之间的函数关系式;(2) 当李华的指距为22cm时,你能预测他的身高吗?
分析:上表3组数据反映了身高y与指距x之间的对应关系,观察这两个变量之间的变化规律,当指距增加1cm,身高就增加9cm,可以尝试建立一次函数模型.
(1) 求身高y与指距x之间的函数表达式;
解得k = 9, b = -20.于是y = 9x -20. ①
将x = 21,y = 169代入①式也符合.公式①就是身高y与指距x之间的函数表达式.
解:当x = 22时, y = 9×22-20 = 178. 因此,李华的身高大约是178 cm.
(2) 当李华的指距为22cm时,你能预测他的身高吗?
2.近几年来,由于经济和社会发展迅速,用电量越来越多.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
⑴请你根据图象所描述的信息,分别求出当0≤x≤50 和x>50时,y与x的函数关系式;
解:当0≤x≤50 时,由图象可设 y=k1x,∵其经过(50,25),代入得25=50k1,∴k1=0.5,∴y=0.5x ;当x>50时,由图象可设 y=k2x+b,∵其经过(50,25)、(100,70),得k2=0.9,b=-20,∴y=0.9x-20.
⑵根据你的分析:当每月用电量不超过50度时,收费标准是多少?当每月用电量超过50度时,收费标准是多少?
解:不超过50度部分按0.5元/度计算,超过部分按0.9元/度计算.
3.小亮和小明周六到距学校24km的滨湖湿地公园春游,小亮8:00从学校出发,骑自行车去湿地公园,小明8:30从学校出发,乘车沿相同路线去滨湖湿地公园,在同一直角坐标系中,小亮和小明的行进路程S(km)与时间t(时)的函数图象如图所示.根据图象得到结论,其中错误的是( )
A.小亮骑自行车的平均速度是12km/hB.小明比小亮提前0.5小时到达滨湖湿地公园C.小明在距学校12km处追上小亮D.9:30小明与小亮相距4km
解:A.根据函数图象小亮去滨湖湿地公园所用时间为10﹣8=2小时,∴小亮骑自行车的平均速度为:24÷2=12(km/h),故正确; B.由图象可得,小明到滨湖湿地公园对应的时间t=9.5,小亮到滨湖湿地公园对应的时间t=10,10﹣9.5=0.5(小时),∴小明比小亮提前0.5小时到达滨湖湿地公园,故正确; C.由图象可知,当t=9时,小明追上小亮,此时小亮离开学校的时间为9﹣8=1小时,∴小亮走的路程为:1×12=12km,∴小明在距学校12km出追上小亮,故正确; D.由图象可知,当t=9.5时,小明的路程为24km,小亮的路程为12×(9.5﹣8)=18km,此时小明与小亮相距24﹣18=6km,故错误;故选D.
4.如图所示,l1反映了某公司产品的销售成本与销售量的关系, l2反映了此公司产品的销售收入与销售量的关系.根据图象填空:
(1)l1对应的表达是 ,l2对应的表达式是 ;(2)当销售量为2吨时, 销售收入= 元,销售成本= 元;(3)当销售量为6吨时,销售收入= 元,销售成本= 元;(4)当销售量 吨时,销售收入等于销售成本;(5)当销售量 吨时,该公司盈利(收入大于成本).当销售 吨时,该公司亏损(收入小于成本).
y=500x+2000
5.在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:(1)甲、乙两根蜡烛燃烧前的高度分别是 ,从点燃到燃尽所用的时间分别是 .
30厘米、25厘米
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;(3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)? 在什么时间段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡烛低?
初中数学苏科版八年级上册6.4 用一次函数解决问题完美版课件ppt: 这是一份初中数学苏科版八年级上册6.4 用一次函数解决问题完美版课件ppt,共55页。PPT课件主要包含了用一次函数解决问题,4练习等内容,欢迎下载使用。
初中数学苏科版八年级上册第六章 一次函数6.4 用一次函数解决问题多媒体教学ppt课件: 这是一份初中数学苏科版八年级上册第六章 一次函数6.4 用一次函数解决问题多媒体教学ppt课件,文件包含64用一次函数解决问题pptx、64用一次函数解决问题2docx、64用一次函数解决问题1docx等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
初中数学苏科版八年级上册第六章 一次函数6.4 用一次函数解决问题集体备课课件ppt: 这是一份初中数学苏科版八年级上册第六章 一次函数6.4 用一次函数解决问题集体备课课件ppt,共11页。PPT课件主要包含了如何解决这个问题,问题2,S105t+35,y2=1200x,解得x>40,变式训练,中考链接等内容,欢迎下载使用。













