初中数学苏科版八年级上册6.4 用一次函数解决问题课堂检测

这是一份初中数学苏科版八年级上册6.4 用一次函数解决问题课堂检测，文件包含第04讲一次函数的实际应用知识解读+题型精讲+随堂检测原卷版docx、第04讲一次函数的实际应用知识解读+题型精讲+随堂检测解析版docx等2份试卷配套教学资源，其中试卷共45页， 欢迎下载使用。

能通过函数图像获取信息，发展形象思维；
能利用函数图像解决简单的实际问题
初步体会方程与函数的关系，建立良好的知识联系
4.通过函数图像解决实际问题，培养学生的数学应用能力，同时培养学生良好的环保意识和热爱生活的意识。
知归纳：
一、分段函数
有的题目中，如下左图，当自变量 x 发生变化时，随着 x 的取值范围不同，y 和 x 的函数关系也不同，它们之间或者不再是一次函数，或者虽然还是一次函数，但函数的解析式发生了变化。这种变化反映在函数图像上时的主要特征，就是由一条直线变成几条线段或射线，我们把这类函数归类为分段函数。
在有的题目中，如下右图，含有两个一次函数的图像，我们需要对两个函数的相关变量进行对比。

二、利用一次函数的知识解应用题的一般步骤
（1）设定实际问题中的变量；
（2）建立一次函数表达式；
（3）确定自变量的取值范围，保证函数具有实际意义；
（4）解答一次函数实际问题，如最大（小）值； （5）写出答案。
【题型1：根式实际问题列除一次函数表达式】
【典例1】（2022秋•东营区校级期末）汽车由北京驶往相距120千米的天津，它的平均速度是30千米/时，则汽车距天津的路程S（千米）与行驶时间t（时）的函数关系及自变量的取值范围是（ ）
A．S＝120﹣30t（0≤t≤4）B．S＝30t（0≤t≤4）
C．S＝120﹣30t（t＞0）D．S＝30t（t＝4）
【答案】A
【解答】解：汽车行驶路程为：30t，
∴车距天津的路程S（千米）与行驶时间t（时）的函数关系及自变量的取值范围是：S＝120﹣30t（0≤t≤4）．
故选：A．
【变式1-1】（2022春•平遥县期中）百货大楼进了一批花布，出售时要在进价（进货价格） 的基础上加一定的利润，其长度x与售价y如下表，下列用长度x表示售价y的关系式中，正确的是（ ）
A．y＝8x+0.3B．y＝（8+0.3）xC．y＝8+0.3xD．y＝8+0.3+x
【答案】B
【解答】解：依题意得：y＝（8+0.3）x；
故选：B．
【变式1-2】（2023•济南二模）学校食堂按如图方式摆放餐桌和椅子．若用x表示餐桌的张数，y表示椅子的把数，请你写出椅子数y（把）与餐桌数x（张）之间的函数关系式 ．
【答案】y＝2x+2
【解答】解：观察图形：x＝1时，y＝4，x＝2时，y＝6；x＝3时，y＝8；…
可见每增加一张桌子，便增加2个座位，
∴x张餐桌共有2x+2个座位．
∴可坐人数y＝2x+2，
故函数关系式可以为y＝2x+2．
故答案为：y＝2x+2．
【变式1-3】（2022春•海口期末）已知一根弹簧在不挂重物时长6cm，在一定的弹性限度内，每挂1kg重物弹簧伸长0.3cm．则该弹簧总长y（cm）随所挂物体质量x（kg）变化的函数关系式为 ．
【答案】y＝0.3x+6
【解答】解：∵每挂1kg重物弹簧伸长0.3cm，
∴挂上xkg的物体后，弹簧伸长0.3xcm，
∴弹簧总长y＝0.3x+6．
故答案为：y＝0.3x+6．
【题型2：利用一次函数解决方案问题】
【典例2】（2023•新市区一模）某鲜花销售公司每月付给销售人员的工资有两种方案．
方案一：没有底薪，只付销售提成；
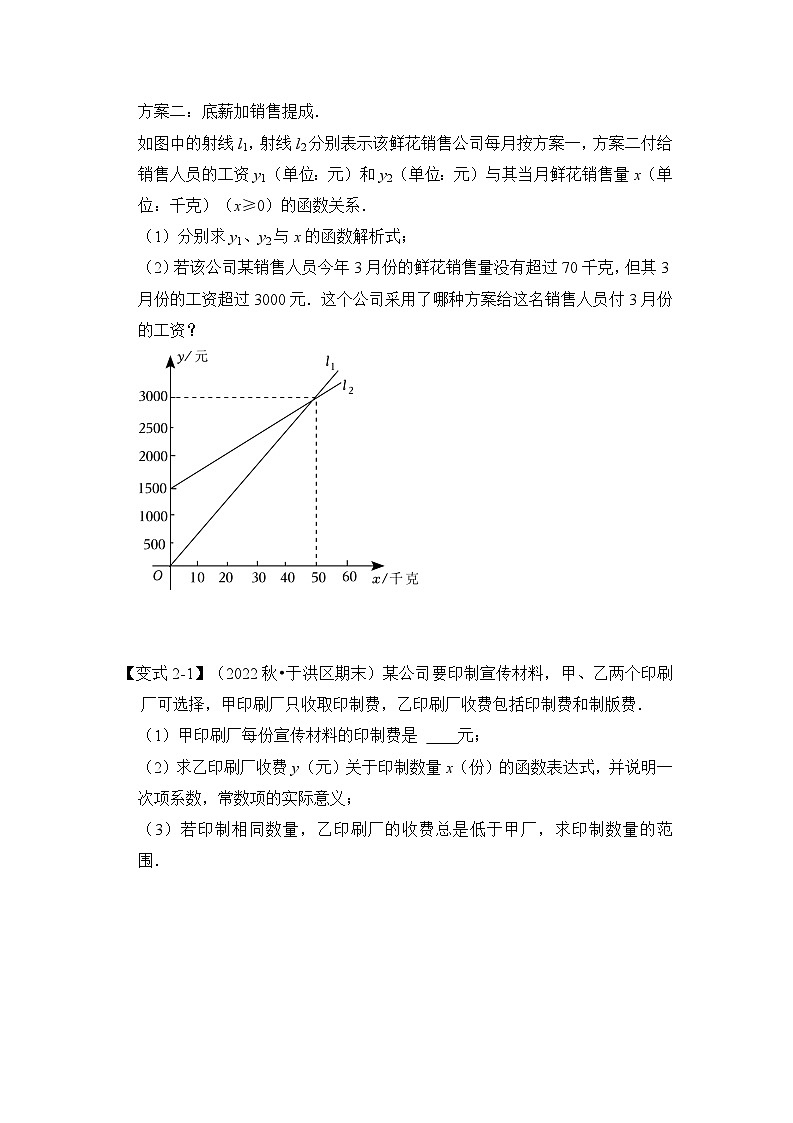
方案二：底薪加销售提成．
如图中的射线l1，射线l2分别表示该鲜花销售公司每月按方案一，方案二付给销售人员的工资y1（单位：元）和y2（单位：元）与其当月鲜花销售量x（单位：千克）（x≥0）的函数关系．
（1）分别求y1、y2与x的函数解析式；
（2）若该公司某销售人员今年3月份的鲜花销售量没有超过70千克，但其3月份的工资超过3000元．这个公司采用了哪种方案给这名销售人员付3月份的工资？
【解答】解：（1）由图可知，y1与x的函数解析式满足正比例函数解析式．
设y1＝k1x（k1≠0），将点（50，2500）代入y1＝k1x（k1≠0），
得50k1＝2500，则k1＝50，则y1＝50x．
设y2与x的函数解析式为y2＝k2x+b（k2≠0），
将点（0，1500）、（50，2500）代入y2＝k2x+b，
得，
于是，
则y2＝20x+1500．
（2）将x＝70分别代入y1、y2，得y1＝50×70＝3500（元），y2＝20×70+1500＝2900（元），
由题可知，其3月工资超过3000元，
∵3500＞3000，
∴这个公司采用方案一给这名销售人员付3月的工资．
【变式2-1】（2022秋•于洪区期末）某公司要印制宣传材料，甲、乙两个印刷厂可选择，甲印刷厂只收取印制费，乙印刷厂收费包括印制费和制版费．
（1）甲印刷厂每份宣传材料的印制费是 2.5 元；
（2）求乙印刷厂收费y（元）关于印制数量x（份）的函数表达式，并说明一次项系数，常数项的实际意义；
（3）若印制相同数量，乙印刷厂的收费总是低于甲厂，求印制数量的范围．
【解答】解：（1）由图或得，甲印刷厂每份宣传材料的印制费为：1000÷400＝2.5（元）．
故答案为：2.5；
（2）设乙印刷厂收费y（元）关于印制数量x（份）的函数表达式为y＝kx+b，
由图可得（0，1500），（400，1900）在图象上，代入，得，
解得：，
∴y＝x+1500，
一次项系数1代表每份宣传材料的印制费为1元，
常数项1500代表制版费为1500元；
（3）由（1）知甲印刷厂每份宣传材料的印制费是2.5元，
∴甲印刷厂收费y（元）关于印制数量x（份）的函数表达式为y＝2.5x，
联立两函数解析式得
解得，
∴两函数图象交点坐标为（1000，2500），
由图象可得当印制数量大于1000时，乙印刷厂的收费总是低于甲厂．
【变式2-2】（2023•禹州市一模）为弘扬爱国精神，传承民族文化，某校组织了“诗词里的中国”主题比赛，计划去某超市购买A，B两种奖品共300个，A种奖品每个20元，B种奖品每个15元，该超市对同时购买这两种奖品的顾客有两种销售方案（只能选择其中一种）．
方案一：A种奖品每个打九折，B种奖品每个打六折．
方案二：A，B两种奖品均打八折．
设购买A种奖品x个，选择方案一的购买费用为y1元，选择方案二的购买费用为y2元．
（1）请分别写出y1，y2与x之间的函数关系式．
（2）请你计算该校选择哪种方案支付的费用较少．
【解答】解：（1）由题意得：y1＝20×0.9x+15×0.6×（300﹣x）＝9x+2700；
y2＝20×0.8x+15×0.8×（300﹣x）＝4x+3600，
∴y1与x之间的函数关系式为y1＝9x+2700，y2与x之间的函数关系式为y2＝4x+3600；
（2）当y1＞y2时，9x+2700＞4x+3600，
解得x＞180，
∴购买A种奖品超过180个时，方案二支付费用少；
当y1＝y2时，9x+2700＝4x+3600，
解得x＝180，
∴购买A种奖品180个时，方案一和方案二支付费用一样多；
当y1＜y2时，9x+2700＜4x+3600，
解得x＜180，
∴购买A种奖品少于180个时，方案一支付费用少．
【题型3：利用一次函数解决销售利润问题】
【典例3】（2022•昭阳区一模）某市雾霾天气趋于严重，甲商场根据民众健康需要，代理销售每台进价分别为600元、560元的A、B两种型号的空气净化器，如表是近两周的销售情况：（进价、售价均保持不变，利润＝销售收入﹣进货成本）
（1）求A，B两种型号的空气净化器的销售单价；
（2）该商店计划一次购进两种型号的空气净化器共30台，其中B型净化器的进货量不超过A型的2倍．设购进A型空气净化器为x台，这30台空气净化器的销售总利润为y元．
①请写出y关于x的函数关系式；
②该商店购进A型、B型净化器各多少台，才能使销售总利润最大？
【解答】解：（1）设A型号空气净化器销售单价为x元，B型号空气净化器销售单价y元，
则，
解得：．
答：A型号空气净化器单价为800元，B型号空气净化器单价780元；
（2）①设A型空气净化器采购x台，采购B种型号空气净化器（30﹣x）台．
则y＝（800﹣600）x+（780﹣560）（30﹣x）＝﹣20x+6600，
∴y与x的关系式为y＝﹣20x+6600；
②∵B型净化器的进货量不超过A型的2倍，
∴30﹣x≤2x，
解得x≥10，
∵y＝﹣20x+6600中，﹣20＜0，
∴当x＝10时，y最大为6400．
此时30﹣x＝20．
答：商店购进A型净化器10台，B型净化器20台时，才能使销售总利润最大．
【变式3-1】（2022秋•武义县期末）非常时期，出门切记戴口罩．当下口罩市场出现热销，某超市老板用1200元购进甲、乙两种型号的口罩在超市俏售，销售完后共获利400元．进价和售价如表：
（1）该超市胸购进甲、乙两种型号口罩各多少袋？
（2）该超市第二次又以原来的进价购进甲、乙两种型号口罩共500袋，此次用于购进口罩的资金不少于1220元，但不超过1360元．若两种型号的口罩都按原来的售价全部售完．设此次购进甲种口罩x袋，超市获利y元，试求y关于x的函数关系式，并求出x的取值范围和超市的最大利润．
【解答】解：（1）根据题意，设甲型号口罩有a袋，乙型号口罩有b袋，用1200元购进，获利400元，
∴，
解方程组得，，
∴甲型号口罩有300袋，乙型号口罩有200袋．
（2）解：以原来的进价购进甲、乙两种型号口罩共500袋，甲种口罩x袋，
∴乙型口罩为（500﹣x）袋，
∵用于购进口罩的资金不少于1220元，但不超过1360元，
∴1220≤2x+3（500﹣x）≤1360，解不等式得，140≤x≤280，
∵获利y元，
∴y＝（3﹣2）x+（3.5﹣3）（500﹣x），整理得，y＝0.5x+250，
∵一次函数y＝0.5x+250中，k＝0.5＞0，
∴函数值y随自变量x的增大而增大，且自变量的取值范围为140≤x≤280，
∴当x＝280时，利润最大，最大值为y＝0.5×280+250＝390（元），
∴y关于x的函数关系式为y＝0.5x+250，且自变量的取值范围为140≤x≤280，当x＝280时，有最大利润，最大利润为390元．
【变式3-2】（2023•市北区校级开学）元旦期间，某经销葡萄的水果店，有两种销售方式：既可以批发，也兼顾零售．店家规定当顾客一次性购买葡萄超过5箱，就可以享受批发价．市场调查显示，这两种销售方式中，每箱葡萄所获利润的情况如表所示：
（1）已知该水果店元旦假期期间，两种销售方式共卖出100箱葡萄，总获利是3600元求元旦假期期间，该水果店这两种方式分别销售了多少箱葡萄；
（2）现该水果店计划销售1000箱葡萄，并规定零售葡萄的数量不超过200箱，若设批发了a箱葡萄，销售1000箱葡萄的总利润为w元，则根据题意，可得w与a的函数关系式为 w＝﹣30a+60000 ；a的取值范围是 800≤a≤1000 ；
（3）忽略其他影响因素．请分析分别零售和批发多少箱葡萄时，才能使售完这1000箱葡萄的总利润最大？求最大总利润是多少元．
【解答】解：（1）设该水果店批发葡萄x箱，则零售葡萄（100﹣x）箱，
由题意，得30x+60（100﹣x）＝3600，
解得x＝80，
答：该水果店批发葡萄80箱，零售葡萄20箱；
（2）由题意，得w＝30a+60（1000﹣a）＝﹣30a+60000，
∴w与a的函数关系式为w＝﹣30a+60000；
∵零售葡萄的数量不超过200箱，
∴1000﹣a≤200，
解得a≥800，
∴a的取值范围是800≤a≤1000，
故答案为：w＝﹣30a+60000；800≤a≤1000；
（3）∵在w＝﹣30a+60000中﹣30＜0，
∴w随x的增大而减小，
∵800≤a≤1000，
∴当a＝800时，w最大，最大值为36000，
此时，1000﹣800＝200，
答：当零售200箱，批发800箱葡萄时，才能使售完这1000箱葡萄的总利润最大，最大总利润是36000元．
【典例4】（2023春•宝丰县月考）“双减”政策颁布后，各校重视了延迟服务，并在延迟服务中加大了体育活动的力度．某体育用品商店抓住商机，计划购进300套乒乓球拍和羽毛球拍进行销售，其中购进乒乓球拍的套数不超过150套，它们的进价和售价如下表：
已知购进2套乒乓球拍和1套羽毛球拍需花费110元，购进4套乒乓球拍和3套羽毛球拍需花费260元．
（1）求出a，b的值；
（2）该面店根据以往销售经验，决定购进乒乓球拍套数不少于羽毛球拍套数的一半，设购进乒乓球拍x（套），售完这批体育用品获利y（元）．
①求y与x的函数关系式，并写出x的取值范围；
②该商店实际采购时，恰逢“双十一”购物节，乒乓球拍的进价每套降低了a元（0＜α∠10），羽毛球拍的进价不变，已知商店的售价不变，这批体育用品能够全部售完，则如何购货才能获利最大？
【解答】解：（1）根据题意：，
解得，
答：a的值为35元，b的值为40元；
（2）①由题意得：
y＝（50﹣35）x+（60﹣40）（300﹣x）＝﹣5x+6000，
∵购进乒乓球拍的套数不超过150套，
∴x≤150，
∵购进乒乓球拍套数不少于羽毛球拍套数的一半，
∴x≥（300﹣x），
解得：x≥100，
则x的取值范围为：100≤x≤150，
∴y与x的函数关系式为y＝﹣5x+6000，x的取值范围为：100≤x≤150；
②由题意得：y＝（50﹣35+a）x+（60﹣40）（300﹣x）＝（a﹣5）x+6000，
∵0＜a＜10，
∴当a＜5即a﹣5＜0时，y随x的增大而减小，
∴当x＝100时，y有最大值，
∴乒乓球拍购进10O套，羽毛球拍购进200套能获利最大；
当a≥5时，即a﹣5≥0时，y随x的增大而增大，
∴当x＝150时，y有最大值，
∴乒乓球拍购进150套，羽毛球拍购进150套能获利最大．
【变式4】（2021秋•南岸区期末）为了切实保护长江生态环境，长江实施全面禁渔．禁渔后，某水库自然生态养殖的鱼在市场上热销，经销商老李每天从该水库购进草鱼和鲢鱼进行销售，两种鱼的进价和售价如表所示：
已知老李购进10斤鲢鱼和20斤草鱼需要160元，购进20斤鲢鱼和10斤草鱼需要140元．
（1）求a，b的值；
（2）老李每天购进两种鱼共300斤，并在当天都销售完，其中销售鲢鱼不少于80斤且不超过120斤，设每天销售鲢鱼x斤（销售过程中损耗不计）．
①求出每天销售获利y（元）与x的函数关系式，并写出x的取值范围；
②元旦节这天，老李让利销售，将鲢鱼售价每斤降低m元（m＞0），草鱼售价全部定为8.5元/斤，为保证元旦节这一天销售这两种鱼获得最小利润，且最小利润为630元，求m的值．
【解答】解：（1）根据题意得：
，
解得；
（2）①由题意得，销售鲢鱼获利y1＝（6﹣4）x＝2x（80≤x≤120），
（Ⅰ）当300﹣x≤200时，100≤x≤120，销售草鱼获利y2＝（9﹣6）×（300﹣x）＝﹣3x+900；
∴当100≤x≤120时，每天销售获利y＝y1+y2＝2x+（﹣3x+900）＝﹣x+900，
（Ⅱ）当300﹣x＞200时，80≤x＜100，销售草鱼获利y2＝（9﹣6）×200+（8.5﹣6）×（300﹣x﹣200）＝﹣2.5x+850；
∴当80≤x＜100时，每天销售获利y＝y1+y2＝2x+（﹣2.5x+850）＝﹣0.5x+850，
综上所述，y＝；
②设销售获利W元，由题意得：W＝（6﹣m﹣4）x+（8.5﹣6）×（300﹣x）＝（﹣0.5﹣m）x+750，其中80≤x≤120，
∵当﹣0.5﹣m≥0时，W＝（﹣0.5﹣m）x+750≥750，不合题意，
∴﹣0.5﹣m＜0，
∴W随x的增大而减小，
∴当x＝120时，W的值最小，
由题意得：（﹣0.5﹣m）×120+750＝630，
解得m＝0.5，
∴m的值为0.5．
【题型4：利用一次函数解决行程问题】
【典例5】（2023春•南关区校级月考）甲车从A地出发匀速驶往B地，半个小时后，乙车沿同一路线由A地匀速驶往B地，两车距A地的路程y（km）与乙车出发时间x（h）之间的函数关系如图所示，根据图象回答下列问题：
（1）乙车速度是 100 km/h，a＝ 40 ；
（2）求甲车距A地的路程y与x之间的函数解析式；
（3）直接写出在乙车行驶过程中，甲、乙两车相距15km时x的值．
【解答】解：（1）由图象知，乙的速度为：＝100（km/h）；
甲的速度为：＝80（km/h），
则a＝80×0.5＝40（km），
故答案为：100，40；
（2）设甲车距A地的路程y与x之间的函数解析式为y＝kx+b （k≠0），
将（0，40）、（5.5，480）代入，得，
解得，
∴甲车距A地的路程y与x之间的函数解析式为y＝80x+40；
（3）设乙车距A地的路程y与x之间的函数解析式为y＝mx（m≠0），
将（4.8，480）代入，得480＝4.8，
解得m＝100，
则乙车距A地的路程y与x之间的函数解析式为y＝100x，
令|80x+40﹣100x|＝15，
解得x1＝，x2＝；
∴当x＝或时，甲、乙两车相距15km．
【变式5-1】（2023•新市区校级一模）甲、乙两车分别从A，B两地去同一城市C，他们离A地的路程y（km）随时间x（h）变化的图象如图所示，根据图象解答下列问题：
（1）A，B两地的路程为 360 千米；
（2）求乙车离A地的路程y（km）关于时间x（h）的函数表达式；
（3）当两车相距20千米时，求乙车行驶的时间．
【解答】解：（1）A，B两地的路程为360千米，
故答案为：360；
（2）设乙离A地的路程y（千米）关于时间x（时）的函数表达式是y＝ax+b，
则，
解得，
∴乙离A地的路程y（千米）关于时间x（时）的函数表达式是y＝80x+40；
（3）设甲离A地的路程y（千米）关于时间x（时）的函数表达式是y＝kx，
把（3，360）代入得：3k＝360，
解得k＝120，
∴甲离A地的路程y（千米）关于时间x（时）的函数表达式是y＝120x，
当两车相距20千米时，|80x+40﹣120x|＝20，
解得x＝或，
当甲到达C地时，80x+40＝340，
解得x＝，
综上所述，当两车相距20千米时，乙车行驶的时间为h或h或h．
【变式5-2】（2023•新华区模拟）小明早晨从家里出发匀速步行去上学，小明的妈妈在小明出发后10min，发现小明的数学课本没带，于是她带上课本立即匀速骑车按小明上学的路线追赶小明，结果与小明同时到达学校，交接课本后立即按原路返回．已知小明距离家的路程s（km）与离开家的时间t（min）之间的函数关系的图象如图所示．
（1）求s（km）与t（min）之间的函数关系；
（2）请在图中画出小明的妈妈距离家的路程s（km）与小明离开家的时间t（min）之间函数关系的图象；（备注：请对画出的图象用数据作适当的标注）
（3）直接写出小明的妈妈在追赶小明及返回家的过程中，距学校0.5km时t的值．
【解答】解：（1）∵s（km）与t（min）之间的函数关系的图像是线段OA，且O（0，0），∴设s＝kt，
又∵A（20，2），
则有：2＝20k，
解得：，
∴．
（2）解：如图1中折线段BA﹣AC．
（3）解：由（2）可知，家与学校的距离为2km，小明妈妈来回学校的时间为20min，
∴小明妈妈的速度为＝0.2km/min，
∴小明的妈妈在追赶小明，距学校0.5km时：，
小明的妈妈在返回家，距学校0.5km时；．
【变式5-3】（2022秋•高邮市期末）甲、乙两地相距150千米，一列快车和一列慢车分别从甲、乙两地同时出发，沿平行的轨道匀速相向而行，快车到达乙地停留一段时间后，按原路原速返回到甲地时停止；慢车到达甲地时停止．慢车到达甲地比快车到达甲地早0.5小时，快车速度是慢车速度的2倍．两车距各自出发地的路程y千米与所用时间x小时的函数图象如图，请结合图象信息解答下列问题：
（1）快车的速度为 100千米/小时 ，慢车的速度为 50千米/小时 ；
（2）求快车返回过程中y与x的函数关系式；
（3）两车出发后经过多长时间相距60千米的路程？
【解答】解：（1）∵快车到达乙地停留一段时间后，按原路原速返回到甲地时停止，慢车到达甲地时停止，
∴图中OA为慢车距乙地的路程y千米与所用时间x小时的函数图象，折线OBCD为快车距甲地的路程y千米与所用时间x小时的函数图象，
∵慢车到达甲地比快车到达甲地早0.5小时，
∴慢车从甲地到乙地所用时间为：3.5﹣0.5＝3（小时），
∴慢车的速度为：（千米/小时），
∵快车速度是慢车速度的2倍，
∴快车速度为50×2＝100（千米/小时）；
故答案为：100千米/小时；50千米/小时．
（2）快车从乙地到甲地所用时间为：（小时），
∴点C的横坐标为3.5﹣1.5＝2，
则C（2，150），
设CD的函数解析式为y＝kx+b（k≠0），
把C（2，150），D（3.5，0）代入得：，
解得：，
∴CD的函数解析式为y＝﹣100x+350，
即快车返回过程中y与x的函数关系式y＝﹣100x+350．
（3）快车从甲地到乙地时，设经过m小时两车相距60千米，
两车相遇前，100m+50m＝150﹣60，
解得：；
两车相遇后，100m+50m＝150+60，
解得：；
快车从乙地出发时，慢车与乙地的距离为：50×2＝100（千米），
快车从乙地到甲地时，设经过n小时，两车相距60千米，根据题意得：100+50n﹣100n＝60，
解得：，（小时）；
综上分析可知，两车出发后经过小时或小时或小时，两车相距60千米的路程．
【题型5：利用一次函数解决运输问题】
【典例6】（2022春•江岸区校级月考）A城有肥料200t，B城有肥料300t，现要把这些肥料全部运往C、D两乡，从A城往C、D两乡运肥料的费元用分别为20元/t和25元/t；从B城往C、D两乡运肥料分别为15元/t和24元/t．现C乡需要肥料240t，D乡需要肥料260t，设A城运往C乡的肥料为x吨，运往C乡肥料的总运费为y1，运往D乡肥料的总运费为y2；
（1）写出y关于x的函数关系式以及y2关于x的函数关系式并指出自变量的取值范围；
（2）怎么样调度使得该过程的总运费最少并求出最少的运输费以及最少的运输方案；
（3）由于从B城到D乡开辟了一条新的公路，使B城到D乡的运输费每吨减少了a（2≤a≤8）元，如何调度才能使总运费最少？最少运输费是多少？（用含a的式子表达）
【解答】解：（1）据题意得：y1＝20x+15（240﹣x）＝5x+3600，
y2＝25（200﹣x）+24（x+60）＝﹣x+6440．
（2）设总运费为y元，
根据题意可得，y与x之间的函数关系为：
y＝5x+3600+（﹣x+6440）＝4x+10040，
∵k＝4＞0，
∴y随x的增大而增大，
∴当x＝0时，y最小＝10040，
∴从A城运往C乡0吨，运往D乡200吨；从B城运往C乡240吨，运往D乡60吨，此时总运费最少，总运费最小值是10040元．
（3）根据题意可知，改善后的总运费为y＝20x+15（240﹣x）+25（200﹣x）+（24﹣a）（x+60）＝（4﹣a）x+10040﹣60a，
∵，
∴0≤x≤200．
①当4﹣a＞0，即2≤a＜4时，y随x的增大而增大，
∴当x＝0时，y最小＝10040﹣60a，
②当4﹣a＜0，即4＜a≤8时，y随x的增大而减小，
∴当x＝200时，y最小＝10840﹣260a，
③当4﹣a＝0时，即a＝4时，无论x去何值，y的值为10040﹣60a．
综上，2≤a≤4时，从A城运往C乡0吨，运往D乡200吨；从B城运往C乡240吨，运往D乡60吨，此时总运费最少，y最小＝10040﹣60a；当4＜a≤8时，从A城运往C乡200吨，运往D乡0吨；从B城运往C乡40吨，运往D乡260吨，此时总运费最少，y最小＝10840﹣260a．
【变式6-1】（2022春•黔东南州期末）A城有肥料200吨，B城有肥料300吨，现全部运往C，D两乡，从A城往C，D两乡运送肥料的费用分别是每吨20元和25元，从B城运往C，D两乡的运输费用分别是15元和24元，C乡需240吨，D乡需260吨，设A城运往C乡的肥料量为x吨，总运费为y元．
（1）求y与x的函数关系式，并写出自变量x的取值范围；
（2）求出总运费最低的调运方案，最低运费是多少？
【解答】解：（1）设总运费为y元，A城运往C乡的肥料量为x吨，则运往D乡的肥料量为（200﹣x）吨；
B城运往C、D乡的肥料量分别为（240﹣x）吨和[260﹣（200﹣x）]＝（60+x）吨，
根据题意得：y＝20x+25（200﹣x）+15（240﹣x）+24（60+x）＝4x+10040，
自变量x的取值范围为0≤x≤200，
∴y与x的函数关系式为y＝4x+10040（0≤x≤200）；
（2）由（1）知，y＝4x+10040，
∵k＝4＞0，
∴y随x的增大而增大，
∴当x＝0时，y最小＝10040，
∴从A城运往C乡0吨，运往D乡200吨；从B城运往C乡240吨，运往D乡60吨，此时总运费最少，总运费最小值是10040元．
【变式6-2】（2022春•武汉期末）2020年春，新冠肺炎疫情暴发后，全国人民众志成城抗击疫情．某省A，B两市成为疫情重灾区，抗疫物资一度严重紧缺，对口支援的C，D市获知A，B两市分别急需抗疫物资200吨和300吨的消息后，决定调运物资支援灾区．已知C市有救灾物资240吨，D市有救灾物资260吨，现将这些抗疫物资全部调往A，B两市．已知从C市运往A，B两市的费用分别为每吨20元和25元，从D市运往往A，B两市的费用别为每吨15元和30元，设从D市运往B市的救灾物资为x吨，并绘制出表：
（1）a＝ x﹣60 ，b＝ 300﹣x ，c＝ 260﹣x （用含x的代数式表示）；
（2）设C，D两市的总运费为w元，求w与x之间的函数关系式，并写出自变量x的取值范围．
（3）由于途经地区的全力支持，D市到B市的运输路线得以改善和优化，缩短了运输时间，运费每吨减少m元（m＞0），其余路线运费不变，若C，D两市的总运费的最小值不小于10320元，求m的取值范围．
【解答】解：（1）∵D市运往B市x吨，
∴D市运往A市（260﹣x）吨，C市运往B市（300﹣x）吨，C市运往A市200﹣（260﹣x）＝（x﹣60）吨，
故答案为：x﹣60，300﹣x，260﹣x；
（2）由题意得：
w＝20（x﹣60）+25（300﹣x）+15（260﹣x）+30x＝10x+10200，
∵x＞0，x﹣60≥0，300﹣x≥0，260﹣x≥0，
∴60≤x≤260，
∴w与x之间的函数关系式为w＝10x+10200，自变量x的取值范围为60≤x≤260；
（3）由题意可得，
w＝10x+10200﹣mx＝（10﹣m）x+10200，
当10﹣m＞0时，即0＜m＜10，
x＝60时，w最小，此时w＝（10﹣m）×60+10200≥10320，
解得0＜m≤8，
当10﹣m＜0时，即m＞10，
x＝260时，w取得最小值，此时w＝（10﹣m）×260+10200≥10320，
解得m≤，
∵＜10，
∴m＞10不符合题意，
∴m的取值范围是0＜m≤8．
1．（2023•聊城）甲乙两地相距a千米，小亮8：00乘慢车从甲地去乙地，10分钟后小莹乘快车从乙地赶往甲地．两人分别距甲地的距离y（千米）与两人行驶时刻t（×时×分）的函数图象如图所示，则小亮与小莹相遇的时刻为（ ）
A．8：28B．8：30C．8：32D．8：35
【答案】A
【解答】解：设小亮与小莹相遇时，小亮乘车行驶了x小时，
∵小亮、小莹乘车行驶完全程用的时间分别是小时，小时，
∴小亮、小莹乘车行驶的速度分别是a千米/时，2a千米/时，
由题意得：ax+2a（x﹣）＝a，
∴x＝，
小时＝28分钟，
∴小亮与小莹相遇的时刻为8：28．
故选：A．
2．（2023•山西）一种弹簧秤最大能称不超过10kg的物体，不挂物体时弹簧的长为12cm，每挂重1kg物体，弹簧伸长0.5cm，在弹性限度内，挂重后弹簧的长度y（cm）与所挂物体的质量x（kg）之间的函数关系式为（ ）
A．y＝12﹣0.5xB．y＝12+0.5xC．y＝10+0.5xD．y＝0.5x
【答案】B
【解答】解：根据题意，得y＝12+0.5x（0≤x≤10），
故选：B．
3．（2023•济南）学校提倡“低碳环保，绿色出行”，小明和小亮分别选择步行和骑自行车上学，两人各自从家同时同向出发，沿同一条路匀速前进．如图所示，l1和l2分别表示两人到小亮家的距离s（km）和时间t（h）的关系，则出发 0.35 h后两人相遇．
【答案】0.35．
【解答】解：设l1的函数解析式为y1＝kx+b，
则，
解得，
∴l1的函数解析式为S1＝5t+3.5；
设l2的函数解析式为S2＝mt，
则0.4m＝6，
解得m＝15，
∴l2的函数解析式为S2＝15t；
令S1＝S2，即5t+3.5＝15t，
解得t＝0.35，
∴出发0.35小时后两人相遇．
故答案为：0.35．
4．（2023•武汉）我国古代数学经典著作《九章算术》记载：“今有善行者行一百步，不善行者行六十步，今不善行者先行一百步，善行者追之．问几何步及之？”如图是善行者与不善行者行走路程s（单位：步）关于善行者的行走时间t的函数图象，则两图象交点P的纵坐标是 250 ．
【答案】250．
【解答】解：由题意可知，不善行者函数解析式为s＝60t+100，
善行者函数解析式为s＝100t，
联立，
解得，
∴两图象交点P的纵坐标为250，
故答案为：250．
5．（2023•威海）一辆汽车在行驶过程中，其行驶路程y（千米）与行驶时间x（小时）之间的函数关系如图所示．当0≤x≤0.5时，y与x之间的函数表达式为y＝60x；当0.5≤x≤2时，y与x之间的函数表达式为 y＝80x﹣10 ．
【答案】y＝80x﹣10．
【解答】解：∵当0≤x≤0.5时，y与x之间的函数表达式为y＝60x，
∴当x＝0.5时，y＝30，
设当0.5≤x≤2时，y与x之间的函数表达式为y＝kx+b，
把（0.5，30），（2，150）代入得：
，
解得，
故答案为：y＝80x﹣10．
6．（2023•陕西）某农科所对当地小麦从抽穗期到灌浆期连续51天的累计需水量进行研究，得到当地每公顷小麦在这51天内累计需水量y（m3）与天数x之间的关系如图所示，其中，线段OA，AC分别表示抽穗期、灌浆期的y与x之间的函数关系．
（1）求这51天内，y与x之间的函数关系式；
（2）求当地每公顷小麦在整个灌浆期的需水量．
【答案】（1）y＝；（2）1085m3．
【解答】解：（1）由题意，当0≤x≤20时，设y＝kx，
∴20k＝960．
∴k＝48．
∴y＝48x．
当20＜x≤51时，设关系式为y＝mx+n，
∴．
∴．
∴y＝35x+260．
综上，所求函数关系式为y＝．
（2）由题意，令x＝51，
∴y＝35×51+260＝2045．
又当x＝20时，y＝960，
∴每公顷小麦在整个灌浆期的需水量＝2045﹣960＝1085（m3）．
7．（2023•齐齐哈尔）一辆巡逻车从A地出发沿一条笔直的公路匀速驶向B地，小时后，一辆货车从A地出发，沿同一路线每小时行驶80千米匀速驶向B地，货车到达B地填装货物耗时15分钟，然后立即按原路匀速返回A地．巡逻车、货车离A地的距离y（千米）与货车出发时间x（小时）之间的函数关系如图所示，请结合图象解答下列问题：
（1）A，B两地之间的距离是 60 千米，a＝ 1 ；
（2）求线段FG所在直线的函数解析式；
（3）货车出发多少小时两车相距15千米？（直接写出答案即可）
【答案】（1）60，1；
（2）线段FG所在直线的函数解析式为y＝﹣60x+120（1≤x≤2）；
（3）货车出发小时或 小时或小时，两车相距15千米．
【解答】解：（1）∵80×＝60（千米），
∴A，B两地之间的距离是60千米；
∵货车到达B地填装货物耗时15分钟，
∴a＝+＝1，
故答案为：60，1；
（2）设线段FG所在直线的解析式为y＝kx+b（k≠0），将F（1，60），G（2，0）代入得：
，
解得 ，
∴线段FG所在直线的函数解析式为y＝﹣60x+120（1≤x≤2）；
（3）巡逻车速度为60÷（2+）＝25（千米/小时），
∴线段CD的解析式为y＝25x+25×＝25x+10（0≤x≤2），
当货车第一次追上巡逻车后，80x﹣（25x+10）＝15，
解得x＝；
当货车返回与巡逻车未相遇时，（﹣60x+120）﹣（25x+10）＝15，
解得x＝；
当货车返回与巡逻车相遇后，（25x+10）﹣（﹣60x+120）＝15，
解得x＝；
综上所述，货车出发小时或 小时或小时，两车相距15千米．
8．（2023•成都）2023年7月28日至8月8日，第31届世界大学生运动会将在成都举行．“当好东道主，热情迎嘉宾”，成都某知名小吃店计划购买A，B两种食材制作小吃．已知购买1千克A种食材和1千克B种食材共需68元，购买5千克A种食材和3千克B种食材共需280元．
（1）求A，B两种食材的单价；
（2）该小吃店计划购买两种食材共36千克，其中购买A种食材千克数不少于B种食材千克数的2倍，当A，B两种食材分别购买多少千克时，总费用最少？并求出最少总费用．
【答案】（1）A种食材单价是每千克38元，B种食材单价是每千克30元；
（2）A种食材购买24千克，B种食材购买12千克时，总费用最少，为1272元．
【解答】（1）设A种食材的单价为x元/千克，B种食材的单价为y元/千克，由题意得：
，
解得：，
∴A种食材单价是每千克38元，B种食材单价是每千克30元；
（2）设A种食材购买m千克，B种食材购买（36﹣m）千克，总费用为w元，由题意得：
w＝38m+30（36﹣m）＝8m+1080，
∵m≥2（36﹣m），
∴24≤m＜36，
∵k＝8＞0，
∴w随m的增大而增大，
∴当m＝24时，w有最小值为：8×24+1080＝1272（元），
∴A种食材购买24千克，B种食材购买12千克时，总费用最少，为1272元．
9．（2023•淮安）快车和慢车同时从甲地出发，以各自的速度匀速向乙地行驶，快车到达乙地卸装货物用时30min，结束后，立即按原路以另一速度匀速返回，直至与慢车相遇，已知慢车的速度为70km/h．两车之间的距离y（km）与慢车行驶的时间x（h）的函数图象如图所示．
（1）请解释图中点A的实际意义；
（2）求出图中线段AB所表示的函数表达式；
（3）两车相遇后，如果快车以返回的速度继续向甲地行驶，求到达甲地还需多长时间．
【答案】（1）A点的实际意义是，出发3小时，快车到达乙地，此时快车与慢车相距120km；
（2）线段AB所表示的函数表达式为y＝﹣70x+330（3≤x≤3.5）；
（3）两车相遇后，如果快车以返回的速度继续向甲地行驶，到达甲地还需2.8h．
【解答】解：（1）A点的实际意义是，出发3小时，快车到达乙地，此时快车与慢车相距120km；
（2）∵点B的横坐标为：3+＝3.5（h），点B的纵坐标为：120﹣×70＝85（km），
∴点B的坐标为（3.5，85），
设线段AB所表示的函数表达式为y＝kx+b，将A（3，120），B（3.5，85）代入得：
，
解得，
∴线段AB所表示的函数表达式为y＝﹣70x+330（3≤x≤3.5）；
（3）快车从返回到遇见慢车所用的时间为：4﹣3.5＝0.5（h），
∴快车从乙地返回甲地时的速度为：85÷0.5﹣70＝100（km/h），
∵4×70÷100＝2.8（h），
∴两车相遇后，如果快车以返回的速度继续向甲地行驶，到达甲地还需2.8h．
10．（2023•青岛）某服装店经销A，B两种T恤衫，进价和售价如下表所示：
（1）第一次进货时，服装店用6000元购进A，B两种T恤衫共120件，全部售完获利多少元？
（2）受市场因素影响，第二次进货时，A种T恤衫进价每件上涨了5元，B种T恤衫进价每件上涨了10元，但两种T恤衫的售价不变．服装店计划购进A，B两种T恤衫共150件，且B种T恤衫的购进量不超过A种T恤衫购进量的2倍．设此次购进A种T恤衫m件，两种T恤衫全部售完可获利W元．
①请求出W与m的函数关系式；
②服装店第二次获利能否超过第一次获利？请说明理由．
【答案】（1）2880元；（2）①W＝﹣4m+3000（150≥m≥50），②服装店第二次获利不能超过第一次获利，理由见详解．
【解答】解：（1）设购进AT恤衫x件，购进BT恤衫y件，根据题意列出方程组为：
，
解得，
∴全部售完获利＝（66﹣45）×80+（90﹣60）×40＝1680+1200＝2880（元）．长度x/m
1
2
3
4
…
售价y/元
8+0.3
16+0.6
24+0.9
32+1.2
…
销售时段
销售数量
销售收入（元）
A种型号（台）
B种型号（台）
第一周
3
2
3960
第二周
5
4
7120
型号
价格
甲型口罩
乙型口罩
进价（元/袋）
2
3
售价（元/袋）
3
3.5
销售方式
每箱所获利润（元）
批发
30
零售
60
进价
售价
乒乓球拍（元/套）
a
50
羽毛球拍（元/套）
b
60
进价（元/斤）
售价（元/斤）
鲢鱼
a
6
草鱼
b
销量不超过200斤的部分
销量超过200斤的部分
9
8.5
A（吨）
B（吨）
合计（吨）
C
a
b
240
D
c
x
260
总计（吨）
200
300
500
品名
A
B
进价（元/件）
45
60
售价（元/件）
66
90