




初中数学苏科版八年级上册6.3 一次函数的图像教课ppt课件
展开1.(2023新疆生产建设兵团中考)一次函数y=x+1的图像不经 过 ( )A.第一象限 B.第二象限C.第三象限 D.第四象限
知识点2 一次函数的性质
解析 在一次函数y=x+1中,k=1>0,b=1>0,∴一次函数y=x+1 的图像经过第一、二、三象限,不经过第四象限.故选D.
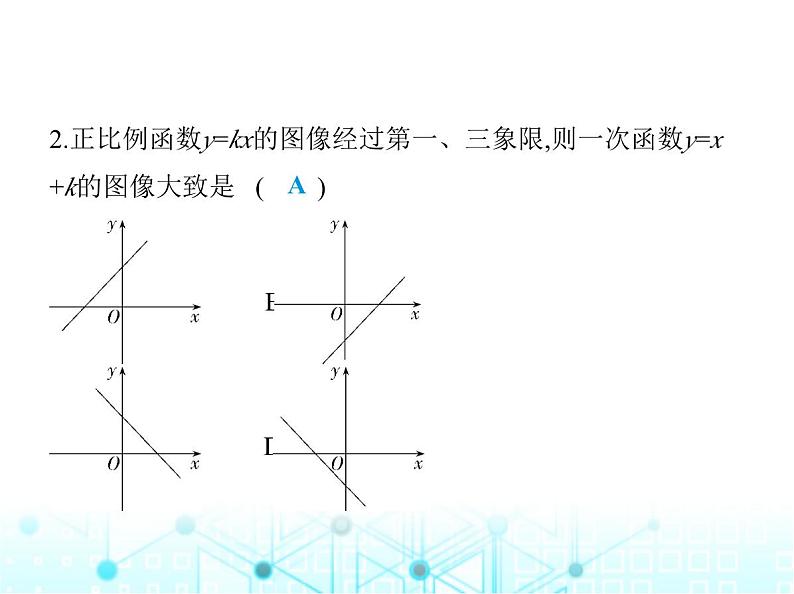
2.正比例函数y=kx的图像经过第一、三象限,则一次函数y=x +k的图像大致是 ( ) A B C D
解析 ∵正比例函数y=kx的图像经过第一、三象限,∴k>0, ∴一次函数y=x+k的图像经过第一、二、三象限.故选A.
3.关于函数y=-2x+3,下列说法中不正确的是 ( )A.该函数是一次函数B.该函数的图像经过第一、二、四象限C.当x值增大时,函数y值也增大D.当x=-1时,y=5
解析 A.函数y=-2x+3符合一次函数的一般形式,故本选项说 法正确;B.∵函数y=-2x+3中,k=-2<0,b=3>0,∴该函数的图像 经过第一、二、四象限,故本选项说法正确;C.∵函数y=-2x+ 3中,k=-2<0,∴当x值增大时,函数y值减小,故本选项说法错误; D.当x=-1时,y=2+3=5,故本选项说法正确.故选C.
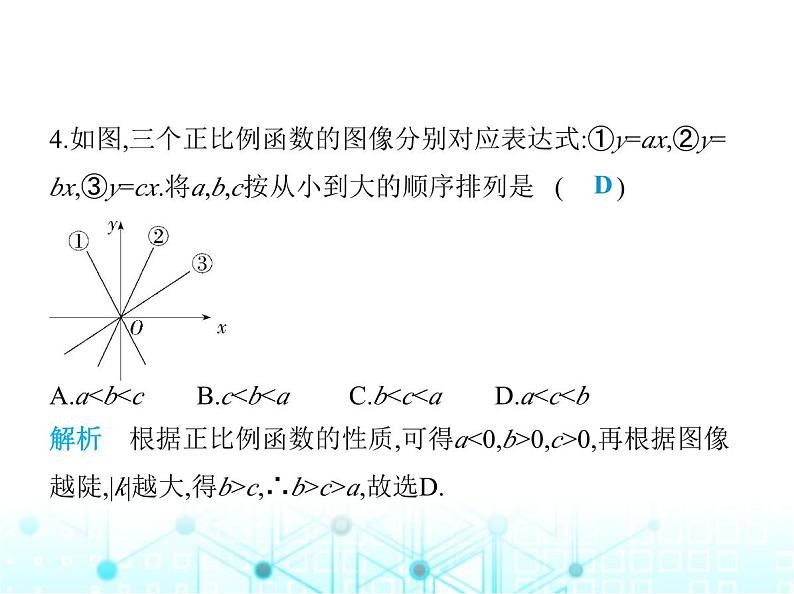
4.如图,三个正比例函数的图像分别对应表达式:①y=ax,②y= bx,③y=cx.将a,b,c按从小到大的顺序排列是 ( ) A.a
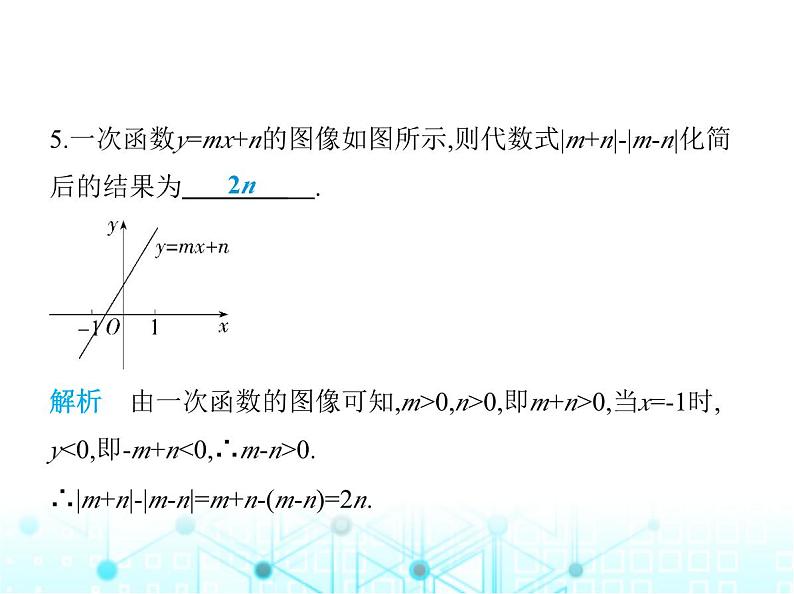
5.一次函数y=mx+n的图像如图所示,则代数式|m+n|-|m-n|化简 后的结果为 .
解析 由一次函数的图像可知,m>0,n>0,即m+n>0,当x=-1时, y<0,即-m+n<0,∴m-n>0.∴|m+n|-|m-n|=m+n-(m-n)=2n.
6.(2022江苏宿迁中考)甲、乙两位同学各给出某函数的一个 特征,甲:“函数值y随自变量x的增大而减小,”乙:“函数图 像经过点(0,2),”请你写出一个同时满足这两个特征的函数, 其表达式是 .
y=-x+2(答案不唯一)
解析 ∵函数值y随自变量x的增大而减小,且该函数图像经 过点(0,2),∴该函数可以为一次函数.设一次函数的表达式为y=kx+2,由题意知k<0,∴k可以取-1,此时一次函数的表达式为y=-x+2.故答案为y=-x+2.(答案不唯一)
7.(教材变式·P154T5)一次函数y=2x+1的图像可由函数y=2x 的图像 ( )A.向上平移1个单位长度得到B.向左平移1个单位长度得到C.向右平移1个单位长度得到D.向下平移1个单位长度得到
解析 由“上加下减”的原则可知,把一次函数y=2x的图像 向上平移1个单位后,所得直线的解析式为y=2x+1.故选A.
知识点3 一次函数图像的平移
8.(一题多解)已知一次函数y=kx+b的图像经过点A(0,-3)和B (1,-1),将该函数图像沿着x轴向右平移3个单位,再向下平移7 个单位得到的函数表达式为 .
解析 解法一:将A(0,-3),B(1,-1)代入y=kx+b,得 解得 ∴一次函数的解析式为y=2x-3.将y=2x-3的图像沿着x轴向右平移3个单位,再向下平移7个单 位得到的函数表达式为y=2(x-3)-3-7=2x-16.解法二:该函数图像沿着x轴向右平移3个单位,再向下平移7 个单位后,点A(0,-3)和B(1,-1)的对应点分别是A'(3,-10)和B'(4,
-8),设经过点A'(3,-10)和B'(4,-8)的函数表达式为y=mx+n(m≠0).把A'(3,-10),B'(4,-8)代入,得 解得 ∴一次函数的解析式为y=2x-16.故答案为y=2x-16.
9.(2024江苏淮安金湖期末,7,★☆☆)一次函数y=ax+b和y=bx +a在同一平面直角坐标系中的图像可能是 ( ) A B C D
解析 当a>0,b>0时,一次函数y=ax+b和y=bx+a的图像均经 过第一、二、三象限;当a>0,b<0时,y=ax+b的图像经过第 一、三、四象限,y=bx+a的图像经过第一、二、四象限;当a< 0,b>0时,y=ax+b的图像经过第一、二、四象限,y=bx+a的图 像经过第一、三、四象限;当a<0,b<0时,y=ax+b和y=bx+a的 图像均经过第二、三、四象限.故选B.
10.(2023陕西中考,5,★☆☆)在平面直角坐标系中,直线y=-x+ m(m为常数)与x轴交于点A,将该直线沿x轴向左平移6个单位 长度后,与x轴交于点A'.若点A'与A关于原点O对称,则m的值 为 ( )A.-3 B.3 C.-6 D.6
解析 ∵直线y=-x+m(m为常数)与x轴交于点A,∴A(m,0),将 该直线沿x轴向左平移6个单位长度后,得到直线y=-(x+6)+m= -x-6+m.∵将该直线沿x轴向左平移6个单位长度后,与x轴交于点A', ∴A'(m-6,0).∵点A'与A关于原点O对称,∴m-6+m=0,解得m=3. 故选B.
11.(新考向·新定义试题)(2024江苏南京高淳月考,7,★☆☆)定义新运算:m⊗n=-mn+n,则对于函数y=x⊗2,下列说法正确的是 ( )A.y随x增大而减小 B.该函数图像经过点(-2,-4)C.当0
12.(2022上海中考,14,★☆☆)已知直线y=kx+b过第一象限且 函数值y随着x的增大而减小,请写出一条符合条件的直线解 析式: .
y=-x+1(答案不唯一)
解析 ∵直线y=kx+b过第一象限且函数值y随着x的增大而 减小,∴k<0,b>0,∴符合条件的函数关系式可以为y=-x+1.故答案为y=-x+1.(答案不唯一)
13.(2020江苏南京中考,13,★★☆)将一次函数y=-2x+4的图像绕原点O逆时针旋转90°,所得到的图像对应的函数表达式是 .
解析 在一次函数y=-2x+4中,令x=0,则y=4,令y=0,则x=2,∴直线y=-2x+4经过点(0,4),(2,0).将一次函数y=-2x+4的图像绕原点O逆时针旋转90°,则点(0,4) 的对应点为(-4,0),(2,0)的对应点是(0,2).设旋转后所得到的图 像对应的函数表达式为y=kx+b(k≠0).将点(-4,0),(0,2)代入,得 解得 ∴旋转后所得到的图像对应的函数表达式为y= x+2.
14.(2022辽宁阜新中考,18,★★☆)当我们将一条倾斜的直线 进行上下平移时,直线的左右位置也发生着变化.下面是关于 “一次函数图像平移的性质”的探究过程,请补充完整.(1)如图,将一次函数y=x+2的图像向下平移1个单位长度,相 当于将它向右平移了 个单位长度.(2)将一次函数y=-2x+4的图像向下平移1个单位长度,相当于 将它向 (填“左”或“右”)平移了 个单 位长度.
(3)综上,对于一次函数y=kx+b(k≠0)的图像而言,将它向下平移m(m>0)个单位长度,相当于将它向 (填“左”或 “右”)(k>0时)或将它向 (填“左”或“右”)(k<0 时)平移了n(n>0)个单位长度,且m,n,k满足等式 .
解析 (1)∵将一次函数y=x+2的图像向下平移1个单位长度 得到y=x+2-1=(x-1)+2,∴相当于将它向右平移了1个单位长 度.故答案为1.(2)将一次函数y=-2x+4的图像向下平移1个单位长度得到y=- 2x+4-1=-2 +4,∴相当于将它向左平移了 个单位长度.故答案为左; .
(3)对于一次函数y=kx+b(k≠0)的图像而言,将它向下平移m (m>0)个单位长度,相当于将它向右(k>0时)或将它向左(k<0 时)平移了n(n>0)个单位长度,且m,n,k满足等式m=n|k|.
15.(运算能力)如图,在平面直角坐标系中,已知A,B两点分别 在x轴,y轴上,OA=OB=4,C在线段OA上,AC=3,过点A作AE⊥ BC,交BC的延长线于E,直线AE交y轴于D.
(1)求点D的坐标.(2)动点P从点A出发,沿射线AO的方向以每秒1个单位长度的速度运动,设点P的运动时间为t秒,△POB的面积为y,求y与t 之间的函数关系式,并直接写出自变量的取值范围.(3)在(2)的条件下,当t=1,PB=5时,在y轴上是否存在一点Q,使 △PBQ是以PB为腰的等腰三角形?若存在,求出点Q的坐标; 若不存在,请说明理由.
解析 (1)∵OA=4,AC=3,∴OC=1.∵BE⊥AE,∴∠EAC+∠ECA=90°,∵∠AOB=90°,∴∠OBC+∠OCB=90°,∵∠ACE=∠BCO,∴∠OBC=∠EAC,又∵∠BOC=∠AOD=90°,BO=AO=4,∴△BOC≌△AOD(ASA).∴OC=OD=1,∴点D的坐标为(0,-1).(2)当0≤t<4时,OP=4-t,
初中数学苏科版八年级上册第六章 一次函数6.3 一次函数的图像教课内容课件ppt: 这是一份初中数学苏科版八年级上册<a href="/sx/tb_c100321_t3/?tag_id=26" target="_blank">第六章 一次函数6.3 一次函数的图像教课内容课件ppt</a>,共14页。
苏科版八年级上册6.3 一次函数的图像授课ppt课件: 这是一份苏科版八年级上册<a href="/sx/tb_c100321_t3/?tag_id=26" target="_blank">6.3 一次函数的图像授课ppt课件</a>,共35页。PPT课件主要包含了y2=2x+3,y3=2x-3等内容,欢迎下载使用。
苏科版八年级上册6.3 一次函数的图像教学演示课件ppt: 这是一份苏科版八年级上册6.3 一次函数的图像教学演示课件ppt,共16页。PPT课件主要包含了自主检测1,上加下减,自主检测2,上加下减左加右减,自主合作,自主检测等内容,欢迎下载使用。













