高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直同步达标检测题

这是一份高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直同步达标检测题，共37页。试卷主要包含了直线与直线垂直，多选题，填空题，解答题等内容，欢迎下载使用。

1 异面直线的定义：不同在任何一个平面内的两条直线叫异面直线。
2．两条异面直线的性质：既不平行，也不相交。
3.空间两条异面直线的画法。
4．异面直线所成的角：
将两条异面直线平移成相交，找到所成的角（所成的角共有4个，两对对顶角，这时根据平面内的两条直线所成角的范围让学生自己猜想应该是那一个角）。

如果两条异面直线夹角等于90°，我们说两条直线垂直
例1如图所示，正方体中，E，F分别为平面与的中心，则与所成角的度数是_____________．
举一反三
1．判断正误．
（1）异面直线所成的角的大小与O点的位置有关．即O点位置不同时，这一角的大小也不同．( )
（2）异面直线a与b所成角可以是．( )
（3）如果两条平行直线中的一条与某一条直线垂直，那么另一条直线也与这条直线垂直．( )
2．如图，在四棱柱中，侧面都是矩形，底面四边形是菱形且，，若异面直线和所成的角为，试求的长.
二．直线与平面垂直
⑴定义：如果一条直线垂直于一个平面内的任意一条直线，那么就说这条直线和这个平面垂直。
⑵判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。
简记为：线线垂直，则线面垂直.
符号：
例2如图所示，A1A是圆柱的母线，AB是圆柱底面圆的直径，C是底面圆周上异于A,B的任意一点，A1A=AB=2.求证:BC⊥平面A1AC．
举一反三
1．如图，在正方体中，E，F分别是棱，的中点，求证：平面EAB．
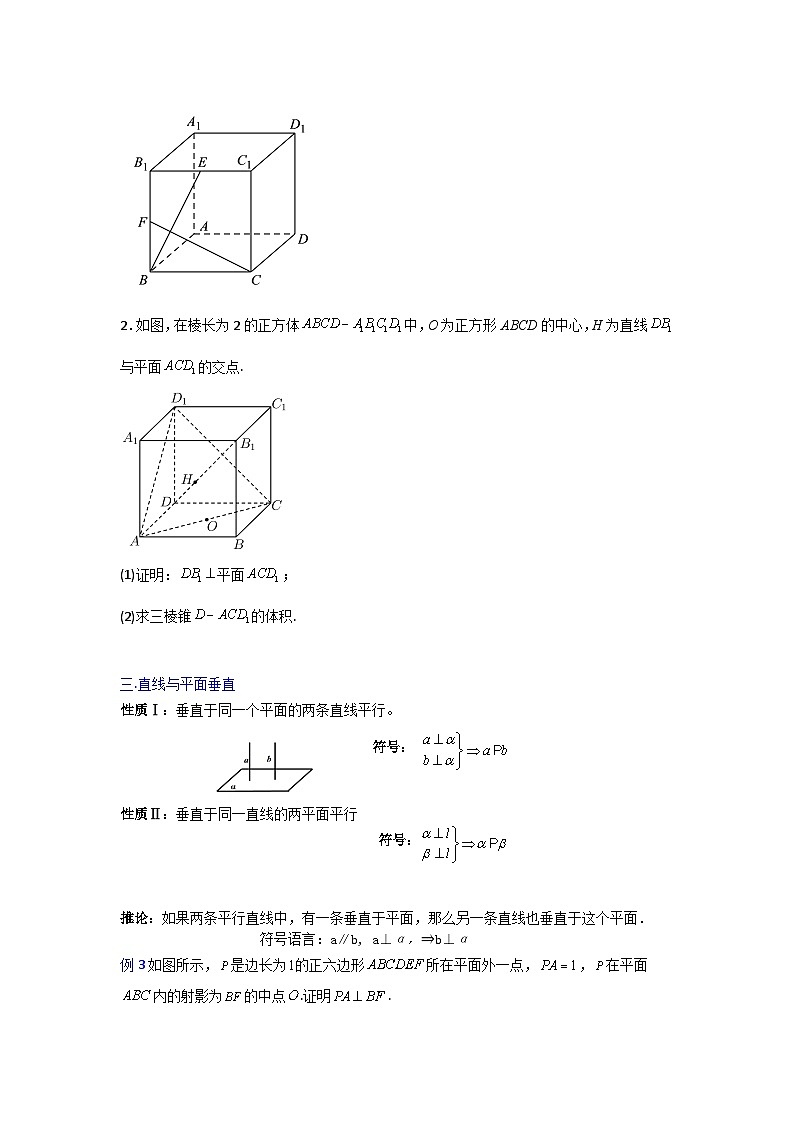
2．如图，在棱长为2的正方体中，O为正方形ABCD的中心，H为直线与平面的交点.
(1)证明：平面；
(2)求三棱锥的体积.
三.直线与平面垂直
性质Ⅰ：垂直于同一个平面的两条直线平行。
符号：

性质Ⅱ：垂直于同一直线的两平面平行
符号：
推论：如果两条平行直线中，有一条垂直于平面，那么另一条直线也垂直于这个平面．
符号语言：a∥b, a⊥α，⇒b⊥α
例3如图所示，是边长为的正六边形所在平面外一点，，在平面内的射影为的中点.证明.
举一反三
1．如图，在三棱锥P-ABC中，，垂足为D，底面ABC，垂足为O,且O在CD上，求证：.
四．平面与平面垂直的判定
⑴定义：两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直。
⑵判定定理：一个平面经过另一个平面的一条垂线，则这两个平面垂直。
简记为：线面面垂直，则面面垂直. 符号：
推论：如果一个平面平行于另一个平面的一条垂线，则这个平面与另一个平面垂直。
例4如图，四棱锥P﹣ABCD的底面为菱形，，平面，且，分别为，的中点，点为棱PC上一动点，
证明：平面平
举一反三
1．如图，正三棱柱中，，，，分别是棱，的中点，在侧棱上，且，求证：平面平面；
2．如图，在四棱锥中，底面为等腰梯形，其中，，，与相交于点，且平面．
(1)证明：平面平面．
(2)若，求点A到平面的距离．
五.平面与平面垂直的性质定理：两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面。
简记为：面面垂直，则线面垂直.

证明线线平行的方法
①三角形中位线 ②平行四边形 ③线面平行的性质 ④平行线的传递性
⑤面面平行的性质 ⑥垂直于同一平面的两直线平行；
证明线线垂直的方法
①定义：两条直线所成的角为90°；（特别是证明异面直线垂直）； ②线面垂直的性质
③利用勾股定理证明两相交直线垂直；
④利用等腰三角形三线合一证明两相交直线垂直；
例59．在三棱锥中，分别为的中点，且.
(1)证明：平面；
(2)若平面平面，证明：.
举一反三
1．如图，在四棱锥P﹣ABCD中，PA＝PD，底面ABCD是矩形，侧面PAD⊥底面ABCD，E是AD的中点．
（1）求证：AD∥平面PBC；
（2）求证：AB⊥平面PAD
2．如图，四边形为正方形，E，F分别为和的中点，以为折痕把折起，使点C到达点P的位置，且平面.
(1)证明：；
(2)若，求三棱锥的体积.
巩固提升
一、单选题
1．设m，n是两条不同的直线，α，β是两个不同的平面，则下列说法正确的是（ ）
A．若m⊥α，n⊂β，m⊥n，则α⊥β
B．若m∥α，m∥n，则n∥α
C．若m∥n，n⊥β，m⊂α，则α⊥β
D．若α⊥β，α∩β＝m，n⊥m，则n⊥β
2．若一个圆锥的侧面积是底面面积的2倍，则该圆锥的母线与其底面所成的角的大小为（ ）
A．B．C．D．
3．已知正方体棱长为，则点到平面的距离为（ ）
A．B．C．D．
4．如图，在四面体D－ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列结论正确的是（ ）
A．平面ABC⊥平面ABD
B．平面ABD⊥平面BDC
C．平面ABC⊥平面BDE，且平面ADC⊥平面BDE
D．平面ABC⊥平面ADC，且平面ADC⊥平面BDE
5．《九章算术》中，将四个面都为直角三角形的三棱锥称为鳖臑（nà）．如图所示的三棱锥为一鳖臑，且平面，平面，若，，，则（ ）
A．B．
C．D．
6．已知平面α⊥平面β，则下列命题中真命题的个数是（ ）
①α内的任意直线必垂直于β内的无数条直线；
②在β内垂直于α与β的交线的直线必垂直于α内的任意一条直线；
③α内的任意一条直线必垂直于β.
A．0B．3C．2D．1
二、多选题
7．已知PA⊥矩形ABCD所在的平面，则下列结论中正确的是（ ）
A．PB⊥BC
B．PD⊥CD
C．PD⊥BD
D．PA⊥BD
8．如图，以等腰直角三角形的斜边上的高为折痕，翻折和，使得平面平面.下列结论正确的是（ ）
A．B．是等边三角形
C．三棱锥是正三棱锥D．平面平面
三、填空题
9．如图，在直四棱柱中，当底面ABCD满足条件___________时，有.（只需填写一种正确条件即可）
10．在《九章算术》中，将四个面都为直角三角形的三棱锥称为“鳖臑”.如图，若三棱锥为“鳖臑”，平面，，，，则此“鳖臑”的表面积为______.
四、解答题
11．如图，在底面是矩形的四棱锥中，底面，，分别是，的中点.
(1)若，求四棱锥的体积；
(2)求证：平面.
12．如图，是正方形，O是正方形的中心，底面，E是的中点．
(1)求证：∥平面；
(2)求证：面面．
13．如图，三棱锥中，AD⊥底面BCD，底面BCD是等边三角形，AD＝BD＝1，M为BC中点.
(1)证明：平面ABC⊥平面ADM；
(2)求点M到平面ABD的距离.
14．在三棱锥A-BCD中，E，F分别是棱BC，CD上的点，且平面ABD.
(1)求证：平面AEF；
(2)若平面BCD，，，记三棱锥F-ACE与三棱锥F-ADE的体积分别为，，且，求三棱锥B-ADF的体积.
15．已知空间几何体ABCDE中，，是全等的正三角形，平面平面BCD，平面平面BCD.
(1)若，求证：；
(2)探索A，B，D，E四点是否共面？若共面，请给出证明；若不共面，请说明理由.
8.6空间直线、平面的垂直（讲义+例题+小练）
一、直线与直线垂直
1 异面直线的定义：不同在任何一个平面内的两条直线叫异面直线。
2．两条异面直线的性质：既不平行，也不相交。
3.空间两条异面直线的画法。
4．异面直线所成的角：
将两条异面直线平移成相交，找到所成的角（所成的角共有4个，两对对顶角，这时根据平面内的两条直线所成角的范围让学生自己猜想应该是那一个角）。

如果两条异面直线夹角等于90°，我们说两条直线垂直
例1如图所示，正方体中，E，F分别为平面与的中心，则与所成角的度数是_____________．
【答案】
【解析】
【详解】
根据题意可知：在中，//，//，
所以在正方体中，
所以与所成角的度数是
故答案为：
举一反三
1．判断正误．
（1）异面直线所成的角的大小与O点的位置有关．即O点位置不同时，这一角的大小也不同．( )
（2）异面直线a与b所成角可以是．( )
（3）如果两条平行直线中的一条与某一条直线垂直，那么另一条直线也与这条直线垂直．( )
【答案】 × × √
【解析】
【详解】
（1）异面直线所成的角的大小与O点的位置无关，故错误；
（2）异面直线a与b所成角不可以是 0°，故错误；
（3）如果两条平行直线中的一条与某一条直线垂直，那么另一条直线也与这条直线垂直，正确.
2．如图，在四棱柱中，侧面都是矩形，底面四边形是菱形且，，若异面直线和所成的角为，试求的长.
【答案】
【解析】
【分析】
连接，得到，根据题意，得到，再求得，，结合，即可求解.
【详解】
如图，连接，在四棱柱中，，，
所以四边形是平行四边形，所以，
所以（或其补角）为和所成的角，
因为异面直线和所成的角为，所以，
因为四棱柱中，侧面都是矩形，底面四边形是菱形，
所以是等腰直角三角形，所以，
因为底面四边形是菱形且，，
所以，，
所以.
二．直线与平面垂直
⑴定义：如果一条直线垂直于一个平面内的任意一条直线，那么就说这条直线和这个平面垂直。
⑵判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直。
简记为：线线垂直，则线面垂直.
符号：
例2如图所示，A1A是圆柱的母线，AB是圆柱底面圆的直径，C是底面圆周上异于A,B的任意一点，A1A=AB=2.求证:BC⊥平面A1AC．
【答案】详见解析.
【分析】
根据直线与平面垂直的判定定理可知,只需证明与平面内的两条相交直线垂直即可,而,满足定理条件.
【详解】
证明:C是底面圆周上异于A,B的任意一点，AB是圆柱底面圆的直径，,
平面平面,,
平面平面
平面.
【点睛】
本题考查直线与平面垂直的判定,考查棱柱的性质,考查学生空间想象能力和推理论证能力,属于中档题.
举一反三
1．如图，在正方体中，E，F分别是棱，的中点，求证：平面EAB．
【答案】见解析
【解析】
【分析】
通过证明和，进而可得证.
【详解】
E，F分别是棱，的中点，
在Rt△和Rt△中，，
所以Rt△ Rt△，所以△，
因为，所以，
所以，即，
又因为正方体中，平面,平面，
所以，和平面EAB内的两条相交直线，
所以平面EAB.
2．如图，在棱长为2的正方体中，O为正方形ABCD的中心，H为直线与平面的交点.
(1)证明：平面；
(2)求三棱锥的体积.
【答案】(1)证明见解析
(2)
【解析】
【分析】
（1）通过面面垂直的判定和性质定理即可得解；
（2）根据三棱锥的体积即可求解.
(1)
解：连接DB，在正方体中，可得,
因为平面，所以平面，
所以,同理可得，
因为平面，所以平面；
(2)
解：三棱锥的体积.
三.直线与平面垂直
性质Ⅰ：垂直于同一个平面的两条直线平行。
符号：

性质Ⅱ：垂直于同一直线的两平面平行
符号：
推论：如果两条平行直线中，有一条垂直于平面，那么另一条直线也垂直于这个平面．
符号语言：a∥b, a⊥α，⇒b⊥α
例3如图所示，是边长为的正六边形所在平面外一点，，在平面内的射影为的中点.证明.
【答案】证明见解析
【解析】
连结，则易知与的交点为，利用线面垂直的判定定理及性质定理，即可得证.
【详解】
证明：连结，则易知与的交点为，如图所示：
由正六边形的性质可得，
∵，，，
∴平面，
∵平面，
∴.
举一反三
1．如图，在三棱锥P-ABC中，，垂足为D，底面ABC，垂足为O,且O在CD上，求证：.
【答案】证明见解析
【解析】
通过线面垂直证得，结合得平面POC，即可得证.
【详解】
证明：底面ABC，底面ABC，.
∵O在CD上,.
又，
平面POC.平面POC，.
【点睛】
此题考查线面垂直的性质和判定的综合应用，利用线面垂直得线线垂直.
四．平面与平面垂直的判定
⑴定义：两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直。
⑵判定定理：一个平面经过另一个平面的一条垂线，则这两个平面垂直。
简记为：线面面垂直，则面面垂直. 符号：
推论：如果一个平面平行于另一个平面的一条垂线，则这个平面与另一个平面垂直。
例4如图，四棱锥P﹣ABCD的底面为菱形，，平面，且，分别为，的中点，点为棱PC上一动点，
证明：平面平
【答案】证明见解析
【解析】
【分析】
利用面面垂直的判定定理即可得到证明
【详解】
连接，
因为底面为菱形，，所以三角形为等边三角形，
因为为的中点，所以
又，所以.
因为平面，平面，所以
因为，所以平面.
又平面，故平面平面
举一反三
1．如图，正三棱柱中，，，，分别是棱，的中点，在侧棱上，且，求证：平面平面；
【答案】证明见解析
【解析】
【分析】
根据定义，在平面中找一条线让其垂直平面即可.
【详解】
在正三棱柱中，平面，平面，则.
是棱的中点，为正三角形，则.
，平面， 平面，.
又，，， ，，
，则 和相似，故，
，则有，故.
，平面，且平面，平面平面.
2．如图，在四棱锥中，底面为等腰梯形，其中，，，与相交于点，且平面．
(1)证明：平面平面．
(2)若，求点A到平面的距离．
【答案】(1)证明见解析；
(2).
【解析】
【分析】
(1)证明，即可；
(2)由等体积即可求.
(1)
如图，过A作，垂足为．
∵为等腰梯形，，，∴，．
∵，∴，∴．
由题意易证，则，
从而，故，即．
∵平面，且平面，∴．
∵，平面，且，∴平面．
∵平面，∴平面平面．
(2)
由(1)可知，，且．
∵平面，∴，．
∵，∴，
则的面积为．
设点A到平面的距离为．
∵，∴，
解得，即点A到平面的距离是
五.平面与平面垂直的性质定理：两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面。
简记为：面面垂直，则线面垂直.

证明线线平行的方法
①三角形中位线 ②平行四边形 ③线面平行的性质 ④平行线的传递性
⑤面面平行的性质 ⑥垂直于同一平面的两直线平行；
证明线线垂直的方法
①定义：两条直线所成的角为90°；（特别是证明异面直线垂直）； ②线面垂直的性质
③利用勾股定理证明两相交直线垂直；
④利用等腰三角形三线合一证明两相交直线垂直；
例59．在三棱锥中，分别为的中点，且.
(1)证明：平面；
(2)若平面平面，证明：.
【答案】(1)证明见解析；
(2)证明见解析.
【解析】
【分析】
（1）由中位线定理，可得，再根据线面平行的判定定理，即可证明结果．
（2）由题意可证，再根据面面垂直的性质定理，可证平面，由此即可证明结果．
(1)
证明:因为，分别为，的中点，
所以，
又平面，平面，
所以平面；
(2)
证明：因为，为的中点，，
又平面平面
平面平面，
所以平面
又平面.
所以.
举一反三
．
1．如图，在四棱锥P﹣ABCD中，PA＝PD，底面ABCD是矩形，侧面PAD⊥底面ABCD，E是AD的中点．
（1）求证：AD∥平面PBC；
（2）求证：AB⊥平面PAD
【答案】（1）证明见解析；（2）证明见解析．
【解析】
【分析】
（1）利用底面是矩形，得到AD∥BC，进而证明AD∥平面PBC；
（2）由AB⊥AD，再由面面垂直的性质定理证明．
【详解】
（1）证明：在四棱锥P﹣ABCD中，∵底面ABCD是矩形，
∴AD∥BC，
又AD平面PBC，BC平面PBC，
∴AD∥平面PBC；
（2）证明：∵底面ABCD是矩形，
∴AB⊥AD，
又∵侧面PAD⊥底面ABCD，侧面PAD平面ABCD＝AD，AB平面ABCD，
∴AB⊥平面PAD.
2．如图，四边形为正方形，E，F分别为和的中点，以为折痕把折起，使点C到达点P的位置，且平面.
(1)证明：；
(2)若，求三棱锥的体积.
【答案】(1)证明见解析
(2)
【解析】
【分析】
（1）由已知可得，及平面平面，可证得平面，即得，则，进而可证得平面，即可证得结果.
（2）过P作，垂足为Q，则平面，利用等体积转化，计算可得结果.
(1)
证明：因为四边形为正方形，E，F分别为和的中点，所以，
又平面平面，且交线为，所以平面，
即.又因为，所以.
又，，所以平面，又在平面内，故.
(2)
过P作，垂足为Q，则平面.
因为，所以，所以，
故.
巩固提升
一、单选题
1．设m，n是两条不同的直线，α，β是两个不同的平面，则下列说法正确的是（ ）
A．若m⊥α，n⊂β，m⊥n，则α⊥β
B．若m∥α，m∥n，则n∥α
C．若m∥n，n⊥β，m⊂α，则α⊥β
D．若α⊥β，α∩β＝m，n⊥m，则n⊥β
【答案】C
【解析】
【分析】
分别根据面面垂直的判定定理，线面平行的判定定理，线面垂直的判定定理判断选项即可.
【详解】
m，n是两条不同的直线，α，β是两个不同的平面，
对于,若m⊥α，n⊂β，m⊥n，则与平行或相交，故错误；
对于,若m∥α，m∥n，则n∥α 或，故错误；
对于,若m∥n，n⊥β，m⊂α，由面面垂直的判定定理可得α⊥β，故正确；
对于,若α⊥β，α∩β＝m，n⊥m，则或与相交或∥，故错误.
故选：.
2．若一个圆锥的侧面积是底面面积的2倍，则该圆锥的母线与其底面所成的角的大小为（ ）
A．B．C．D．
【答案】C
【解析】
【分析】
设圆锥的底面半径为，母线长为，由题意求出，利用线面角的定义求解即可．
【详解】
解：设圆锥的底面半径为，母线长为，
因为圆锥的侧面积是底面积的2倍，
所以，
解得，
设该圆锥的母线与底面所成角，
则，
所以．
故选：C
3．已知正方体棱长为，则点到平面的距离为（ ）
A．B．C．D．
【答案】B
【解析】
【分析】
作出辅助线，证明出AC⊥平面，找到点到平面的距离即CE的长，求出答案.
【详解】
连接AC交BD于点E，则因为四边形ABCD为正方体，所以AC⊥BD，且E为AC中点，因为⊥底面ABCD，平面ABCD，所以⊥，因为，所以AC⊥平面，所以CE的长即为点到平面的距离，因为正方体棱长为2，所以由勾股定理可得：，显然.
故选：B
4．如图，在四面体D－ABC中，若AB＝CB，AD＝CD，E是AC的中点，则下列结论正确的是（ ）
A．平面ABC⊥平面ABD
B．平面ABD⊥平面BDC
C．平面ABC⊥平面BDE，且平面ADC⊥平面BDE
D．平面ABC⊥平面ADC，且平面ADC⊥平面BDE
【答案】C
【解析】
【分析】
利用垂直关系，结合面面垂直的判断定理，即可判断选项.
【详解】
因为AB＝CB，且E是AC的中点，所以BE⊥AC，同理有DE⊥AC，于是AC⊥平面BDE.因为AC在平面ABC内，所以平面ABC⊥平面BDE.又由于AC⊂平面ACD，所以平面ACD⊥平面BDE.
故选：C
5．《九章算术》中，将四个面都为直角三角形的三棱锥称为鳖臑（nà）．如图所示的三棱锥为一鳖臑，且平面，平面，若，，，则（ ）
A．B．
C．D．
【答案】A
【解析】
【分析】
根据平面， 平面求解.
【详解】
因为平面， 平面，
所以，
又，，，
所以,
所以，
故选：A
6．已知平面α⊥平面β，则下列命题中真命题的个数是（ ）
①α内的任意直线必垂直于β内的无数条直线；
②在β内垂直于α与β的交线的直线必垂直于α内的任意一条直线；
③α内的任意一条直线必垂直于β.
A．0B．3C．2D．1
【答案】C
【解析】
【分析】
根据面面垂直的性质定理可判断①②；α内不与交线垂直的直线不垂直于β，由此判断③.
【详解】
①已知平面α⊥平面β，设α∩β＝l，设a为内任意一直线，在β内作b⊥l，则，
而 ，故，
故β内与b平行的无数条直线均垂直于 内的任意直线，即α内的任意直线必垂直于β内的无数条直线，故①为真命题；
②因为平面α⊥平面β，故 β内垂直于α与β交线的直线必垂直于平面α，则它垂直于α内的任意直线，故②为真命题；
③平面α⊥平面β时，α内不与交线垂直的直线必不垂直于β，故③为假命题,
故选;C.
二、多选题
7．已知PA⊥矩形ABCD所在的平面，则下列结论中正确的是（ ）
A．PB⊥BC
B．PD⊥CD
C．PD⊥BD
D．PA⊥BD
【答案】ABD
【解析】
【分析】
由矩形，得，若，则平面，又平面，则过平面外一面有两条直线与平面垂直，不成立，故不正确．
【详解】
解：矩形，矩形，
，故正确．
若，则平面，
又平面，则过平面外一面有两条直线与平面垂直，
故不正确，故不正确；
矩形，
，，
平面，，故正确；
矩形，
由三垂线定理得，故正确；
故选：．
8．如图，以等腰直角三角形的斜边上的高为折痕，翻折和，使得平面平面.下列结论正确的是（ ）
A．B．是等边三角形
C．三棱锥是正三棱锥D．平面平面
【答案】ABC
【解析】
【分析】
利用面面垂直以及线面垂直的性质可判断A选项；设，利用勾股定理可判断B选项；利用正棱锥的定义可判断C选项；利用面面垂直的性质结合面面垂直的性质可判断D选项.
【详解】
对于A选项，翻折前，因为，为的中点，则，
翻折后，对应地有，
因为平面平面，平面平面，平面，
所以，平面，因为平面，故，A对；
对于B选项，设，翻折前，因为为等腰直角三角形，
为的中点，则，且，，
由勾股定理可得，
翻折后，因为平面，平面，则，
由勾股定理得，
在三棱锥中，，则为等边三角形，B对；
对于C选项，在三棱锥中，因为为等边三角形，，
故三棱锥为正三棱锥，C对；
对于D选项，假设平面平面，如下图所示：
取的中点，连接、，因为，为的中点，则，
若平面平面，因为平面平面，平面，
所以，平面，
设等边的中心为点，连接，由正棱锥的性质可知，平面，
因为过点作平面的垂线，有且只有一条，故假设不成立，
即平面与平面不垂直，D错.
故选：ABC.
三、填空题
9．如图，在直四棱柱中，当底面ABCD满足条件___________时，有.（只需填写一种正确条件即可）
【答案】(答案不唯一)
【解析】
【分析】
直四棱柱，是在上底面的投影，当时，可得，当然底面ABCD满足的条件也就能写出来了.
【详解】
根据直四棱柱可得：∥，且，所以四边形是矩形，所以∥，同理可证：∥，当时，可得：，且底面，而底面，所以，而，从而平面，因为平面，所以，所以当满足题意.
故答案为：.
10．在《九章算术》中，将四个面都为直角三角形的三棱锥称为“鳖臑”.如图，若三棱锥为“鳖臑”，平面，，，，则此“鳖臑”的表面积为______.
【答案】
【解析】
【分析】
根据“鳖臑”的定义和已知数据可求得，，，从而可求出其表面积
【详解】
因为平面，平面，
所以,
因为，，
所以平面，
因为平面，所以，
因为，，
所以，，，
所以“鳖臑”的表面积为
.
故答案为：
四、解答题
11．如图，在底面是矩形的四棱锥中，底面，，分别是，的中点.
(1)若，求四棱锥的体积；
(2)求证：平面.
【答案】(1)
(2)证明详见解析
【解析】
【分析】
（1）根据锥体的体积公式，即可求出结果；
（2）根据线面垂直的判定定理，即可证明面，又由中位线定理，可得，进而证明出结果.
(1)
解：∵在底面是矩形的四棱锥中，底面，，
∴；
(2)
证明：∵四边形为矩形，
∴，
∵底面，面，
∴，
又，∴面，
又，分别是，的中点，
∴，
∴平面.
12．如图，是正方形，O是正方形的中心，底面，E是的中点．
(1)求证：∥平面；
(2)求证：面面．
【答案】(1)证明见解析
(2)证明见解析
【解析】
【分析】
(1)连接AC交BD于O，连接OE，由中位线即可得，得证；
(2)证明BD⊥平面PAC即可.
(1)
连接AC，交BD于O，连接OE，
在△CAP中，，∴，
又∵平面BDE，平面BDE，∴∥平面BDE；
(2)
∵PO⊥底面ABCD，则PO⊥BD，
又∵是正方形，则AC⊥BD，且，∴BD⊥平面PAC.
∵平面PBD，∴平面PAC⊥平面PBD.
13．如图，三棱锥中，AD⊥底面BCD，底面BCD是等边三角形，AD＝BD＝1，M为BC中点.
(1)证明：平面ABC⊥平面ADM；
(2)求点M到平面ABD的距离.
【答案】(1)证明见解析
(2)
【解析】
【分析】
（1）根据线面垂直的判定定理，证明BC⊥平面ADM,再根据面面垂直的判定定理证明平面ABC⊥平面ADM；
（2）根据，即利用等体积法求得答案.
(1)
证明：∵AD⊥底面BCD，∴AD⊥BC,
又∵底面BCD为等边三角形，M为BC中点，∴DM⊥BC,
且，平面ADM,
∴BC⊥平面ADM,
又平面ABC，∴平面ABC⊥平面ADM；
(2)
设点M到平面ABD的距离为d，
,
由得：，
即 ，
故，
∴点M到平面ABD的距离为.
14．在三棱锥A-BCD中，E，F分别是棱BC，CD上的点，且平面ABD.
(1)求证：平面AEF；
(2)若平面BCD，，，记三棱锥F-ACE与三棱锥F-ADE的体积分别为，，且，求三棱锥B-ADF的体积.
【答案】(1)证明见解析
(2)
【解析】
【分析】
（1）根据平面ABD，利用线面平行的性质定理得到，再利用线面平行的判定定理证明；
（2）根据，，，得到，再根据平面，由求解.
(1)
证明：∵平面ABD，平面BCD，平面平面，
∴，
又∵平面AEF，平面AEF，
∴平面AEF；
(2)
∵，，且，
∴，
∴，
∴，
由（1）知，
∴，又因为，
所以，
所以 ，
因为平面，
所以.
15．已知空间几何体ABCDE中，，是全等的正三角形，平面平面BCD，平面平面BCD.
(1)若，求证：；
(2)探索A，B，D，E四点是否共面？若共面，请给出证明；若不共面，请说明理由.
【答案】(1)证明见解析
(2)证明见解析
【解析】
【分析】
（1）先利用正三角形和勾股定理得到线线垂直，再利用面面垂直、线面垂直的性质进行证明；
（2）分别取，中点，，连接，，根据正三角形得到线线垂直，进而利用面面垂直的性质得到线面垂直，再利用线面垂直得到线线平行，再利用平行关系进行证明.
(1)
解： 因为、是全等的正三角形，所以，
又因为，所以，故，
因为平面平面，且平面平面，
所以平面， 又因为平面，
所以；
(2)
解：，，，四点共面，理由如下：
分别取，中点，，连接，，
因为是等边三角形，所以，，
因为平面平面，
所以平面，
同理平面，且，
所以，且，
所以四边形是平行四边形，
所以，又，
所以，即，，，四点共面．